Этапы решения задач на ЭВМ.

Решение задачи разбивается на этапы:

1. Постановка задачи
2. Формализация (математическая постановка)
3. Выбор (или разработка) метода решения
4. Разработка алгоритма
5. Составление программы
6. Отладка программы
7. Вычисление и обработка результатов

1. При постановке задачи выясняется конечная цель и вырабатывается общий подход к решению задачи. Выясняется сколько решений имеет задача и имеет ли их вообще. Изучаются общие свойства рассматриваемого физического явления или объекта, анализируются возможности данной системы программирования.
2. На этом этапе все объекты задачи описываются на языке математики, выбирается форма хранения данных, составляются все необходимые формулы.
3. Выбор существующего или разработка нового метода решения (очень важен и, в то же время личностный этап).
4. На этом этапе метод решения записывается применительно к данной задаче на одном из алгоритмических языков (чаще на графическом).
5. Переводим решение задачи на язык, понятный машине.

1.2. Алгоритм. Свойства алгоритмов.

Алгоритм - это определенным образом организованная последовательность действий, за конечное число шагов приводящая к решению задачи.
Свойства алгоритмов:

1. Определенность
2. Дискретность
3. Целенаправленность
4. Конечность
5. Массовость

Порядок выполнения алгоритма:

1. Действия в алгоритме выполняются в порядке их записи
2. Нельзя менять местами никакие два действия алгоритма
3. Нельзя не закончив одного действия переходить к следующему

Для записи алгоритмов используются специальные языки:

1. Естественный язык (словесная запись)
2. Формулы
3. Псевдокод
4. Структурограммы
5. Синтаксические диаграммы
6. Графический (язык блок-схем)

1. Естественный язык:
   если условие то действие1 иначе действие2
2. Структурограмма:
   
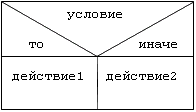
3. Синтаксическая диаграмма:
   
4. Графический язык:
   

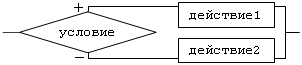
Составление алгоритмов графическим способом подчиняется двум ГОСТам:

1. ГОСТ 19.002-80, соответствует международному стандарту ИСО 2636-73. Регламентирует правила составления блок-схем.
2. ГОСТ 19.003-80, соответствует международному стандарту ИСО 1028-73. Регламентирует использование графических примитивов.

Название	Символ (рисунок)	Выполняемая функция (пояснение)
1. Блок вычислений		Выполняет вычислительное действие или группу действий
2. Логический блок		Выбор направления выполнения алгоритма в зависимости от условия
3. Блоки ввода/вывода		Ввод или вывод данных вне зависимости от физического носителя
	Вывод данных на печатающее устройство
4. Начало/конец (вход/выход)		Начало или конец программы, вход или выход в подпрограмму
5. Предопределенный процесс		Вычисления по стандартной или пользовательской подпрограмме
6. Блок модификации		Выполнение действий, изменяющих пункты алгоритма
7. Соединитель		Указание связи между прерванными линиями в пределах одной страницы
8. Межстраничный соединитель		Указание связи между частями схемы, расположенной на разных страницах

Правила построения блок-схем:

1. Блок-схема выстраивается в одном направлении либо сверху вниз, либо слева направо
2. Все повороты соединительных линий выполняются под углом 90 градусов

1.3. Алгоритмическая конструкция ветвления.

Ветвление - управляющая структура, организующая выполнение лишь одного из двух указанных действий в зависимости от справедливости некоторого условия.
Условие - вопрос, имеющий два варианта ответа: да или нет.
Запись ветвления выполняется в двух формах: полной и неполной.
Полная форма:

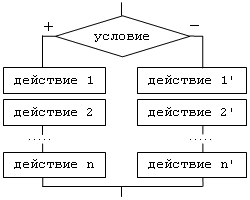
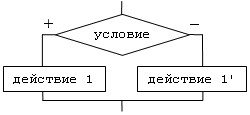
Неполная форма:

Пример: найти наименьшее из трех чисел.
1 вариант решения:

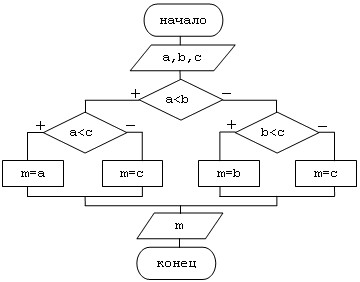
2 вариант решения:

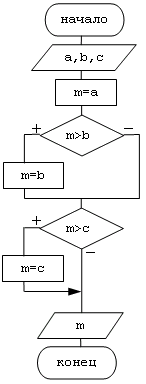
1.4. Алгоритмическая конструкция цикла.

Цикл - управляющая структура, организующая многократное выполнение указанного действия.

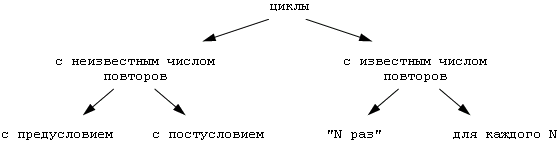
Цикл " пока":

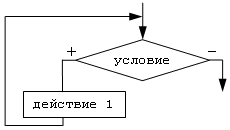
Выполнение цикла " пока" начинается с проверки условия, поэтому такую разновидность циклов называют циклы с предусловием. Переход к выполнению действия осуществляется только в том случае, если условие выполняется, в противном случае происходит выход из цикла. Можно сказать что условие цикла " пока" - это условие входа в цикл. В частном случае может оказаться что действие не выполнялось ни разу. Условие цикла необходимо подобрать так, чтобы действия выполняемые в цикле привели к нарушению его истинности, иначе произойдет зацикливание.
Зацикливание - бесконечное повторение выполняемых действий.
Цикл " до":

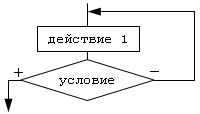
Исполнение цикла начинается с выполнения действия. Таким образом тело цикла будет реализовано хотя бы один раз. После этого происходит проверка условия. Поэтому цикл " до" называют циклом с постусловием. Если условие не выполняется, то происходит возврат к выполнению действий. Если условие истинно, то осуществляется выход из цикла. Таким образом условие цикла " до" - это условие выхода. Для предотвращения зацикливания необходимо предусмотреть действия, приводящие к истинности условия.
Цикл с параметром, или цикл со счетчиком, или арифметический цикл - это цикл с заранее известным числом повторов.

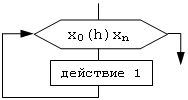
В блоке модификации указывается закон изменения переменной параметра.
Xo - начальное значение параметра
h - шаг
Xn - последнее значение параметра
Для создания циклов с параметром необходимо использовать правила:

1. Параметр цикла, его начальное и конечное значения и шаг должны быть одного типа
2. Запрещено изменять в теле цикла значения начальное, текущее и конечное для параметра
3. Запрещено входить в цикл минуя блок модификации
4. Если начальное значение больше конечного, то шаг - число отрицательное
5. После выхода из цикла значение переменной параметра неопределенно и не может использоваться в дальнейших вычислениях
6. Из цикла можно выйти не закончив его, тогда переменная параметр сохраняет свое последнее значение

1.5. Использование циклов с параметром для обработки массивов.

Массив - упорядоченная структура, предназначенная для хранения однотипных данных.
Упорядочение элементов в массиве происходит по их индексам.
Индекс - порядковый номер элемента.
Массив задается именем (заглавные латинские буквы), типом данных и размерностью.
Размерность - максимально возможное количество элементов в массиве. В один момент времени можно обратиться только к одному элементу массива. Для этого указывается имя массива и в скобках индекс элемента.
Массивы делятся на одномерные (линейные) и двумерные.
Прообразом в математике для одномерного массива является вектор. Для двумерного - матрица.
Пример: вычислить n!

Пример: вычислить aⁿ

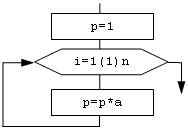
Пример: ввести элементы массива:
а)одномерного, размерности 10

б)двумерного, 5x5