
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Десятичные дроби.
|
|
п.4.1 Определение десятичной дроби, свойства десятичных дробей.
п.4.2 Преобразование обыкновенных дробей в десятичные.
п.4.3 Действия над десятичными дробями.
п.4.4 Бесконечные периодические дроби и их преобразование в обыкновенные.
4.1 Определение десятичной дроби, свойства десятичных дробей.
Распространим запись натуральных чисел в 10-чной позиционной системе на рациональные числа.
Вспомним, что каждое натуральное число n единственным образом представляется в виде суммы различных неотрицательных степеней числа 10, умноженных на некоторые коэффициенты ai, т.е.
(1) n=ak*10k+ak-1*10k-1+…+a1*10+a0, где n€N, 0 ≤ аi ≤ 10-1или иначе.
Вся суть позиционной системы обусловлена записью: m=ak ak-1…a1a0 при которой удобны алгоритмы арифметических действий над натуральными числами.
По аналогии с записью (1) составим сумму:
(2) r= ak*10k + ak-1*10k-1+…+a1*10+a0 +  +
+ 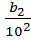 +…+
+…+ 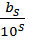 где, 0≤ ai, bi≤ 9, ( цифры )
где, 0≤ ai, bi≤ 9, ( цифры )
Очевидно, что число r как сумма натуральных чисел и рациональных или обыкновенных дробей является рациональным числом.
По аналогии с короткой записью натуральных чисел число r можно представить короткой записью: (3) r=ak ar-1 …a1a0, b1b2…bs, где запятойотделена целая часть от дробной.
Действительно, если в записи (2) привести слагаемые к общему знаменателю, получим
r = 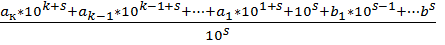
Таким образом, иначе число r можно представить в виде равенства (4),
r= 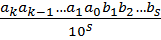 =
=  n
n 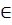 N0, s
N0, s 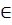 N.
N.
Поскольку в числителе складываются степени 10 от  до 100, то числитель выражается в обычной десятичной системе счисления.
до 100, то числитель выражается в обычной десятичной системе счисления.
Таким образом (4) равенство представлено рациональным числом, которое иначе можно записать как r = 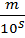 n
n 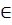 N0, s
N0, s 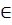 N. r – неотрицательное рациональное число.
N. r – неотрицательное рациональное число.
Очевидно, что аналогичным образом можно представить и отрицательное рациональное число такого же вида:
(5) r=-ak ar-1 …a1a0, b1b2…bs = 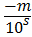 , т.о. рациональное число может быть представлено в виде обыкновенной дроби: r =
, т.о. рациональное число может быть представлено в виде обыкновенной дроби: r = 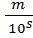 , m
, m  Z, s
Z, s 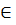 N.
N.
Определение: Конечной десятичной дробью называется обыкновенная
десятичная дробь со знаменателем, равным степени 10, т.е.
 , m
, m  Z, s
Z, s 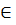 N. Обычно используют короткую запись (3) или (5).
N. Обычно используют короткую запись (3) или (5).
Например: 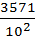 =
= 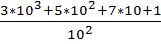 =3*10+5+
=3*10+5+ 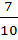 +
+ 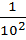 =35, 71
=35, 71
Определение: Цифры стоящие после запятой в десятичной дроби называются десятичными знаками, их количество равно показателю степени 10.
Рассмотрим несколько свойств десятичных дробей, которые вытекают из их определения:
10. Из 2-х рядом стоящих цифр в записи десятичной дроби левая цифра имеет разрядную единицу в 10 раз большую, чем правая (r=…a1*10+a0*100…)
20. Умножение десятичной дроби на 10n достигается переносом запятой на n цифр вправо, а деление влево.
Справедливость этого свойства можно определить сравнением равенств (3) и (4). Умножим число r*10n 4… 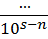 (количество десятичных знаков уменьшается на n, а это значит, что (3) мы должны перенести запятую на n знаков вправо).
(количество десятичных знаков уменьшается на n, а это значит, что (3) мы должны перенести запятую на n знаков вправо).
r=  =
= 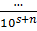 Этого же можно достичь (3) переносом запятой на n знаков.
Этого же можно достичь (3) переносом запятой на n знаков.
30. Приписывание нулей в десятичной дроби и отбрасывание нулей стоящих в конце десятичной дроби, не изменяя ее значения.
Действительно, если в равенстве (3) приписывать в конце нули, то это равносильно прибавлению к сумме 2 слагаемых вида 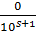 +
+ 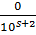 , которые не меняют значения суммы 2 следовательно и не меняется и дробь (3).
, которые не меняют значения суммы 2 следовательно и не меняется и дробь (3).
Аналогично обратное, если bs=0, то равенство (2) заканчивается слагаемым 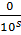 , которое не влияет на значение суммы 2. Значит в равенстве (3) ноль можно отбросить и значение не изменится.
, которое не влияет на значение суммы 2. Значит в равенстве (3) ноль можно отбросить и значение не изменится.
40. Для приведения 2-х десятичных дробей к одинаковому знаменателю достаточно приписывать к той десятичной дроби, у которой меньше десятичных знаков, столько нулей, чтобы количество десятичных знаков в дробях было одинаково.
Действительно, каждый приписываемый нуль увеличивает знаменатель дроби в 10 раз, но не изменяет значение этой дроби.
Поскольку все десятичные дроби можно считать приведенными к общему знаменателю, то их легко сравнить по знаменателю. Из двух дробей с равными знаменателями больше та, у которой больше числитель.
50. Из 2-х положительных десятичных дробей больше та, у которой больше целая часть; если целые части равны, то больше та у которой больше 1-ый из неравных десятичных знаков. (3, 345< 3, 354)
Можем привести к общему знаменателю по предыдущему свойству, то сравнение десятичных дробей сводится к сравнению целых чисел стоящих в числителе(4) (т.е. сравнение обыкновенной дроби).
По аналогии с целыми числами любая положительная десятичная дробь больше отрицательной. Из отрицательной больше, та модуль, которой меньше.(-1, 247> -2, 427).
п.2 Преобразование десятичных дробей в десятичные.
Мы знаем, что любое натуральное число можно представить в виде десятичной записи (1). Будет ли это утверждение верно для десятичной записи (2) любого рационального числа?
Пусть 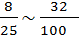 =0, 32,
=0, 32, 
Теорема: Для того, чтобы несократимую дробь можно было представить конечной десятичной дробью, необходимо и достаточно чтобы в разложении ее знаменателя на простые множители входили только простые числа 2 и 5.
Доказательство:
Достаточность. Пусть n=2r*5s. Предположим, что r≥ s и представим дробь: 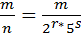 умножим знаменатель дроби на 5r-s.
умножим знаменатель дроби на 5r-s. 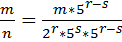 =
= 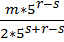 =
= 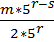 =
= 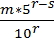
т.е. дробь в этом случае конечная десятичная дробь. ЧТД
Если r< s, то достаточно числитель и знаменатель дроби умножить на 2s-r
Необходимость. Пусть несократимая дробь 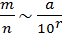 представляется в виде конечной десятичной дроби: (*)
представляется в виде конечной десятичной дроби: (*)  =
= 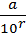 .
.
Докажем, что в разложении знаменателя n имеются только на простые множители: 2 и 5. Предположим противное, что в разложении n имеется простой множитель p n⁞ p, p=2, 5.
Запишем равенство  =
= 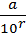 , т.о. m*10r=a*n, по нашему предположению n⁞ p, тогда произведение (a*n)⁞ p, тогда, на p делится (m*10r) ⁞ p, но 10r≠ p т.к. (p≠ 2, 5) значит m⁞ p( свойство делимости произведения)
, т.о. m*10r=a*n, по нашему предположению n⁞ p, тогда произведение (a*n)⁞ p, тогда, на p делится (m*10r) ⁞ p, но 10r≠ p т.к. (p≠ 2, 5) значит m⁞ p( свойство делимости произведения)  - сократима, что противоречит условию теоремы. ЧТД.
- сократима, что противоречит условию теоремы. ЧТД.
Пример:  =
= 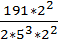 =
=  ;
;  =0, 75.
=0, 75.
п.3 Действия над десятичными дробями.
Сравнение десятичных дробей и выполнение арифметических действий с ними сводится по существу к сравнениям и действиям над ЦЧ. Действительно чтобы сложить две десятичные дроби, согласно правилу сложения рациональных чисел, достаточно привести к общему знаменателю и сложить числители.
Пример:  +
+ 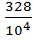 = 7, 8628.
= 7, 8628.
Если использовать свойства десятичных дробей, то можно было эти дроби сложить столбиком (приписывание нулей)
7, 8300
+ 0, 0328
7, 8328
В общем виде правило сложения (вычитания) десятичной дроби моет быть сформулировано следующим образом:
Чтобы сложить (вычесть) 2 десятичные дроби нужно:
1) Уровнять в этих десятичных дробях количество десятичных знаков после запятой;
2) Не принимая во внимание запятую, сложить (вычесть) получившиеся числа;
3) В результате отделить столько знаков, сколько отделено в каждой из десятичных дробей.
Замечание: При выполнении действий столбиком нули в конце десятичной дроби не записывают, при уравнении десятичных знаков достаточно записать дроби столбиком так чтобы единицы одного разряда находились в одном столбике, т.е. запятая числа стояла под запятой.
Правило 2 (сравнения)
Чтобы сравнить две десятичные дроби надо уровнять в них количество десятичных знаков после запятой, отбросить запятую и сравнить получившиеся целые числа.
Пример: 3, 62517 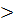 3, 623, т.к. 362517
3, 623, т.к. 362517 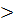 362300
362300
Для того чтобы уяснить алгоритм умножения десятичной дроби, запишем дроби в виде обыкновенных, в общем случае они имеют вид
 , m, n € Z, k, s € N тогда
, m, n € Z, k, s € N тогда
Перемножим 2 обыкновенные дроби по правилу:
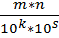 =
= 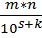 , таком образом при умножение десятичной дроби в целом числе
, таком образом при умножение десятичной дроби в целом числе  следует отделить запятой
следует отделить запятой  десятичных знаков.
десятичных знаков.
Правило 3. Чтобы перемножить две десятичные дроби, следует перемножить их как целые числа (не принимая во внимание запятые) и в произведение отделить запятой количество десятичных знаков, равное сумме десятичных знаков в сомножителях
Например: 60, 003
2, 1
60 003
120 006
126, 0063
Поскольку умножение десятичных дробей, является частичным случаем умножения обыкновенных десятичных дробей, то для десятинных дробей умножение ассоциативно и коммуникативно и дистрибутивно относительно сложения и вычитания. (записать формулы)
Рассмотрим деление десятинных дробей. Множество десятичных дробей замкнуто относительно деления. Запишем две десятичные дроби в виде обыкновенных, уже приведенных к общему знаменателю, тогда
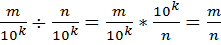 (*)
(*)
Если дробь  , после сокращения, будет иметь знаменатель, делящийся хотя бы на одно простое число, отличное от 2 и 5, что по Т1 (п.4.2) она не представима в виде конечной десятичной дроби.
, после сокращения, будет иметь знаменатель, делящийся хотя бы на одно простое число, отличное от 2 и 5, что по Т1 (п.4.2) она не представима в виде конечной десятичной дроби.
Т.О. множество конечных десятичных дробей не замкнуто относительно деления.
Предположим, что в нашем редком случае (т.к. простых чисел бесконечно много) результатом деления (*) представим в виде десятичной дроби, т.е. 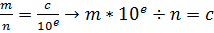 - деление целых чисел.
- деление целых чисел.
Последнее равенство описывает в общих чертах правило деления десятичных дробей:
1. В делители запятую надо перенести в конец числа (сделать делитель целым);
2. При этом в делимом надо перенести запятую на такое же количество десятичных знаков;
3. Осуществить деление уголком, при этом запятая в частном предоставляется в момент исчерпания целой части делимого.
Пример: 1). 24, 252: 14, 1=1, 72
24, 252 14, 1
141 172
987 При этом в делимом приписывают нули столько
282 раз, пока деление не закончится (10n)
282 5, 2: 0, 5=10, 4
2). 1, 21: 0, 33=121: 33= 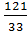
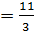 - частное не может быть выражено десятичной дробью (конечной).
- частное не может быть выражено десятичной дробью (конечной).
п.4.4 Бесконечные периодические дроби и их преобразование в обыкновенные.
Рассмотрим дробь  , ее нельзя представить конечной десятичной дробью (почему?) Однако, поделив 2 на 9 будем иметь 0, 2
, ее нельзя представить конечной десятичной дробью (почему?) Однако, поделив 2 на 9 будем иметь 0, 2 
0, 22 <  < 0, 23 т.д.
< 0, 23 т.д.
А кратко записывают 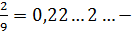 бесконечная десятичная дробь.
бесконечная десятичная дробь.
Если отбросить все цифры, начиная с некоторой, то получим число <  , а если увеличить последнюю цифру на 1, то
, а если увеличить последнюю цифру на 1, то  .
.
Определение 3: Бесконечный ряд чисел вида a0, b1b2…bn…, где a0 целое число, а каждое из bi (i=1, 2…) принимает одно из значений 0, 1…9 называется бесконечной десятичной дробью.
Бесконечной десятичной дробью называется периодической, если содержит в своей записи после запятой повторяющуюся группу цифр, называемую периодом.
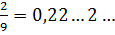 =0, (2)
=0, (2)
Период принято записывать в скобках. Количество цифр в периоде называется его длиной. Всякую конечную десятичную дробь можно рассматривать как бесконечную периодическую: 0, 15=0, 1500…=0, 15(0).
Теорема 2. Любое рациональное число представимо бесконечной периодической десятичной дробью.
Доказательство: Пусть рациональное число r представлено дробью 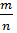 m € Z, n € N, (m, n=1).
m € Z, n € N, (m, n=1).
Если n=  *
* 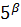 то теорема доказана в силу теоремы 1.
то теорема доказана в силу теоремы 1.
Если знаменатель n содержит в разложении простой множитель, отличный о 2 и 5, то процесс деления m на n закончится не может, поскольку в противном случае получится конечная десятичная дробь и противоречие теореме 1. Таким образом, в этом случае десятичная запись рационального числа r =  представляется бесконечной десятичной дробью.
представляется бесконечной десятичной дробью.
Покажем, что это дробь будет периодической. Для определенности будем считать, что n> m> 0. Умножим m на 10 и разделим на n, применяя теорему о делимости с остатком 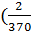 )
)
10*m= n*q1+r1, 0< r1< n/
Очевидно, что q1 – цифра. В противном случае, при q1 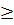 10 будем иметь 10m
10 будем иметь 10m 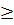 10n+r1 или 10(m-n)
10n+r1 или 10(m-n) 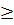 r1 , но m-n< 0, а r1> 0 получим противоречие.
r1 , но m-n< 0, а r1> 0 получим противоречие.
Далее разделим 10r1 на n, получим 10r1=n*q2+r2, 0< r2< n, 0  .
.
И т.д. получим бесконечную последовательность равенств:
10m=n*q1+r1 где все 0< r1< n, а 0 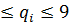 . т.е. десятичные
. т.е. десятичные
10r1=n*q2+r2 знаки, возникающие при записи числа 
10r2=n*q3+r3 (6) десятичной дробью 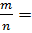 0, q1q2q3 …qk qk+1 … (7)
0, q1q2q3 …qk qk+1 … (7)
…………………
10rk-1=n*qk+rk
10rk=n*qk+1+rk+1
В равенстве (6) остатки ri начиная с некоторого шага начнут повторяться, поскольку неравенству 0< ri< n удовлетворяет n-1 натуральных чисел: 1, 2, 3…n-1, а процесс получения остатков бесконечен.
Но равенство ri=rk повлечет последующие равенства qi+1=qk+1 и ri+1=rk+1 и т.д. Это означает, что как только в равенствах(6) два остатка совпали, то частные начинают повторяться, остатки тоже повторяются, а бесконечная десятичная дробь(7) является периодической. Теорема доказана.
Пример: Записать числа 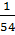 =0, 0(185)
=0, 0(185)
100 54
54 0, 01851…
…
Определение: Бесконечная периодическая десятичная дробь называется частной периодической, если период начинается сразу после запятой. В противном случае дробь называется смешанной. 0, (27) 2, 32(27)
Можно доказать, что если знаменатель не сократимой дроби  взаимно прост с 10 (т.е. в разложение n не входит 2 и 5), то дробь
взаимно прост с 10 (т.е. в разложение n не входит 2 и 5), то дробь 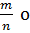 бращается в чисто периодическую дробь.
бращается в чисто периодическую дробь.
Например: 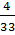 =(0, 12) 33=3*11
=(0, 12) 33=3*11
40 33
33 0, 121…
Если у несократимой дроби  знаменатель n=
знаменатель n= 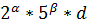 , где (d, 10)=1, то при обращение дроби
, где (d, 10)=1, то при обращение дроби  в десятичную, получается смешанная периодическая бесконечная дробь с количеством цифр между запятой и периодом (предпериодом) равным max
в десятичную, получается смешанная периодическая бесконечная дробь с количеством цифр между запятой и периодом (предпериодом) равным max  .
.
Например: 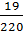 =0, 08(63) 220=22*5*11
=0, 08(63) 220=22*5*11
1900 220
1760 0, 086363…
Справедливо обратная теорема
Теорема. Любая бесконечная периодическая дробь, не имеющая 9 периодом, выражает некоторое рациональное число.
Рассмотрим процесс преобразования периодических дробей в обыкновенные. Первоначально преобразуем в обыкновенную чистую периодическую дробь.
Пусть r=0, q1q2…qn…( 8) Обозначим натуральное число q1q2…qn=a Умножим равенство (8) на 10n, получим
10n*r=0, (q1q2…qn)*10n;
10n*r=a+0, (q1q2…qn)=a+r
Откуда r(10n -1)=a, следовательно r= 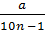 (9).
(9).
Очевидно 10n-1 –число, записываемое с помощью n девяток. ММИ докажем.
Можем сформулировать правило 1.
Чтобы преобразовать в обыкновенную чистую периодическую дробь, следует в числителе записать число, образованное цифрами периода, а в знаменатель записать число, образованное девятками, количество которых равно длине периода.
Замечание: мы рассмотрели дробь с нулевой целой частью, т.к. a0, b1b2…bn…= a0+0, b1b2…bn… Если 0, b1b2…bn…=  , то a0, b1b2…bn…= a0+
, то a0, b1b2…bn…= a0+ 
Пример: 1)0, 1212…= 0, (12) =  =
= 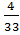
2)0, 031031…=0, (031)= 
Пусть теперь (10) r=0, q1q2…qn(q1+nq2+n…qn+k) смешанная периодическая дробь с предпериодом из n цифр и периодом из k цифр. Обозначим:
a=q1+nq2+n…qn+k , b=q1q2…qn
Умножим равенство (10) на 10n, получим 10n*r= b+0, (q1+nq2+n…qn+k)
Полученное равенство умножим на 10h
10h*10n*r=b*10k+a+0, (qn+1…qn+k) или по(9) 10n+k*r=b+10k+a+ 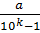
или 10n+k*r=b+10k+  , т.е. 10n+k*r=b+10k+
, т.е. 10n+k*r=b+10k+ 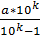 .
.
Откуда: r= 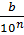 +
+ 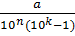 или
или
r= 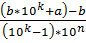
Таким образом, получим следующее правило 2:
Чтобы преобразовать в обыкновенную смешанную периодическую дробь, следует в числителе записать разность между числом, образованным цифрами, стоящими до второго периода, и числом, образованным предпериодом. В знаменателе надо записать число, образованное таким количеством девяток, сколько цифр в периоде, и таким количеством нулей, сколько цифр в предпериоде.
Пример: 0, 02(34)= 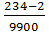 =
= 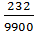 =
= 
0, 1(03)= 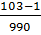 =
= 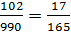
|