Вероятность попадания случайной точки в заданную область.

Пусть имеется система случайных величин (X, Y), причем известна ее плотность распределения f(x, y). Требуется найти вероятность попадания случайной точки в заданную область D (рис.3.6).

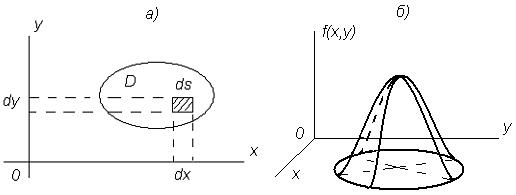
Рисунок 3.6 Вероятность попадания случайной точки в заданную область D (а); поверхность распределения f(x, y) (б)

Для расчета вероятности попадания случайной точки (x, y) в

область D введем понятие «элемент вероятности». Элемент вероятности

системы случайных величин (X, Y) есть вероятность попадания случайной точки (x, y) в элементарный прямоугольник со сторонами dx и dy. Тогда вероятность попадания случайной точки (x, y) в область D (рис. 3.6а) можно определить по формуле

.

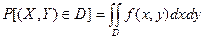Плотность распределения системы двух случайных величин обладает следующими свойствами:

а) плотность распределения f(x, y) есть функция неотрицательная

,

б) двойной несобственный интеграл с бесконечными пределами от плотности распределения системы двух случайных величин равен единице, т.е.

.

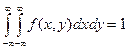Геометрически первое свойство означает, что поверхность распределения располагается выше плоскости x0y, а второе – что, объем тела, ограниченного поверхностью распределения и плоскостью x0y, равен единице (рис.3.6б).