Линейная регрессия.

Рассмотрим двумерную случайную величину (X, Y), где X и Y – зависимые случайные величины.

Представим приближенно одну случайную величину как функцию другой. Точное соответствие невозможно. Будем считать, что эта функция линейная.

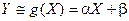
Для определения этой функции остается только найти постоянные величины a и b.

Определение. Функция g(X) называется наилучшим приближением случайной величины Y в смысле метода наименьших квадратов, если математическое ожидание

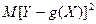принимает наименьшее возможное значение. Также функция g(x) называется среднеквадратической регрессией Y на X.

Теорема. Линейная средняя квадратическая регрессия Y на Х вычисляется по формуле:

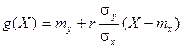
в этой формуле m_x=M(X), m_y=M(Y), 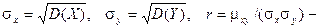коэффициент корреляции величин Х и Y.

Величина 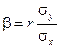называется коэффициентом регрессии Y на Х.

Прямая, уравнение которой

,

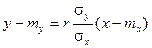называется прямой сренеквадратической регрессии Y на Х.

Величина 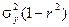называется остаточной дисперсией случайной величины Y относительно случайной величины Х. Эта величина характеризует величину ошибки, образующейся при замене случайной величины Y линейной функцией g(X) =a Х + b.

Видно, что если r=± 1, то остаточная дисперсия равна нулю, и, следовательно, ошибка равна нулю и случайная величина Y точно представляется линейной функцией от случайной величины Х.

Прямая среднеквадратичной регрессии Х на Y определяется аналогично по формуле:

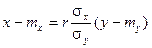
Прямые среднеквадратичной регрессии пересекаются в точке (т_х, т_у), которую называют центром совместного распределения случайных величин Х и Y.