Объём многогранника и его свойства

Объёмом многогранника называется положительная величина, которая для каждого многогранника определяется следующим образом:

1)

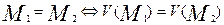
Равные многогранники имеют равные объёмы.

2)

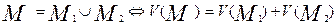
Если многогранник состоит из конечного числа многогранников, то объём этого многогранника будет равен сумме объёмов многогранников, его составляющих.

Объединение многогранников составлено таким образом, что пересечением этих многогранников является некоторая поверхность F.

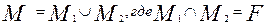
Измерение объёма многогранника

Для того чтобы измерить объёма многогранника:

1) выбирают единицу измерения – куб с ребром, равным единице длины е, тогда объёмом единичного куба будет .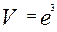

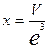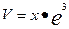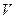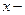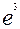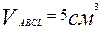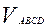2) находят отношение объёма измеряемого многогранника к объёму единичного куба. - это отношение является числовым значением объёма измеряемого многогранника. Результат измерения записывается в виде произведения , где - объём измеряемого многогранника, числовое значение объёма измеряемого многогранника, - объём единичного куба. Например, , где - объём измеряемого многогранника, 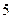- числовое значение объёма измеряемого многогранника, 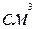- объём единичного куба.

Свойства объёма

1. Равные многогранники имеют равные числовые значения объёмов этих многогранников при одной и той же единице измерения.

1. Если многогранник состоит из конечного числа многогранников, то числовое значение объёма этого многогранника равно сумме числовых значений объёмов многогранников, его составляющих при одной и той же единице измерения.

1. Если единица измерения объёма увеличится (уменьшится) в несколько раз, то числовое значение объёма уменьшится (увеличится) во столько же раз. Например, 5 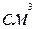=500 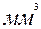, единица измерения уменьшилась, а числовое значение увеличилось в 100 раз.

5 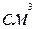=0, 05 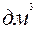, единица измерения увеличилась, числовое значение

уменьшилось в 100 раз.

Теорема об измерении объёма прямоугольного параллелепипеда

Числовое значение объёма прямоугольного параллелепипеда равно произведению числовых значений трёх его измерений.

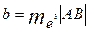
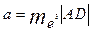)= abc, гд е

Время

В обыденной жизни время – это то, что отделяет одно событие от другого. В математике и физике время рассматривают как скалярную величину, потому что промежутки времени обладают свойствами, похожими на свойства длины, площади и массы.

Промежутки времени можно складывать (например, 5ч+2ч=7ч), вычитать (например, 8ч 30мин-12мин=8ч18мин), умножать на положительное действительное число (например, 45мин*4=180мин=3ч).

Промежутки времени измеряют, но процесс измерения времени отличается от процесса измерения длины. Промежуток времени, принятый за единицу. Может быть использован лишь один раз. Поэтому, единицей измерения должен быть регулярно повторяющийся процесс. Такой единицей в СИ названии секунда. Есть и другие единицы: минута, час, сутки, неделя, месяц, год, век. Чтобы вести счёт, надо иметь начало отсчёта. У времени нет начала и конца. Поэтому, чтобы считать, нужно самим установить начало счёта. Например, рождение Христа принято считать в христианстве началом новой эры – начало отсчёта времени.

Рассматриваются задачи на время трёх видов:

• Нахождение длительности события

Например: «Урок начинается в 10.00, а заканчивается в 10.45. Сколько длится урок?»

Начало события: 10.00-начало урока

Конец события: 10.45 – конец урока

Длительность события: 10.45-10.00=45 мин – длительность урока.

Чтобы найти длительность события, надо из конца события вычесть начало события.

• Нахождение начала события

Например: «Урок длится 45 минут и заканчивается в 10.45. В котором часу начинается урок?»

Конец события: 10.45 – конец урока

Длительность события: 45 мин – длительность урока.

Начало события: 10.45-00.45=10.00-начало урока

Чтобы найти начало события. Надо из конца события вычесть длительность события.

• Нахождение конца события

Например: «Урок начинается в 10.00 и длится 45 минут. В котором часу закончится урок?»

Начало события: 10.00-начало урока

Длительность события: 45 мин – длительность урока.

Конец события: 10.00+00.45=10.45 – конец урока

Чтобы найти конец события, надо к началу события прибавить длительность события.

Задачи на время связаны с двумя понятиями:

• Календарное время (Время, которое на данный момент показывает календарь и часы. Например, 2 марта 2011года, 17.40).
• Арифметическое время (Время, которое показывает, сколько прошло от начала летоисчисления, от начала года, о начала суток до данного момента. Например, от начала летоисчисления прошло полных 2010 лет, от начала года – 2 месяца, от начала месяца – 1 день, от начала суток – 17 часов, от начала часа 40 минут)