
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дробные реплики
|
|
При увеличении числа факторов в факторных экспериментах типа 2k или 3k число наблюдений, необходимых для полной реплики плана, быстро перерастает возможности большинства исследователей. Для полной реплики плана 2 6 необходимо 64 наблюдения; в этом плане из 63 степеней свободы только 6 соответствуют главным эффектам и только 15 — двухфакторным взаимодействиям, остальные 42 степени свободы приходятся на взаимодействия трех и более факторов. В экспериментах типа 3k например, для плана 3 5 требуется 243 наблюдения, и из 242 степеней свободы лишь 10 соответствуют главным эффектам.
Если экспериментатор с достаточным основанием может считать некоторые из взаимодействий высокого порядка пренебрежимо малыми, то информацию о главных эффектах и взаимодействиях низкого порядка можно получить, проведя лишь дробную долю полного факторного эксперимента. Такие дробные факторные эксперименты нашли широкое применение при исследованиях в промышленности. Одним из основных приложений дробных факторных планов являются отсеивающие эксперименты; в них исследуется много факторов одновременно, для того чтобы выделить из них (если таковые окажутся) факторы, обладающими большими эффектами. Отсеивающие эксперименты проводятся обычно на ранних этапах исследования, причем часто оказывается, что большинство исходных факторов практически не влияет на отклик.
Факторы, которые, как устанавливается, являются важными, исследуются затем более тщательно в последующих экспериментах.
10.1 Полуреплика плана типа 2 k
Рассмотрим ситуацию, когда интерес представляют три фактора на двух уровнях каждый, но ограниченные возможности не позволяют экспериментатору проверить все 23 = 8 комбинаций обработок. Он может, однако, провести четыре наблюдения, что наводит на мысль о полуреплике плана 23. Поскольку такой план содержит 23-1 = 4 комбинации обработок, то полуреплика плана 23 часто называется планом 23-1.
Таблица 6 представляет собой таблицу алгебраических знаков для плана 23. Допустим, что в качестве нашей полуреплики мы выбрали четыре комбинации обработок а, b, с и abc (они приведены в верхней половине таблицы). Для комбинаций обработок мы будем использовать как обычные обозначения (а, b, с), так и обозначения с помощью алгебраических знаков; соответствие между ними следующее:
Обозначение 1 Обозначение 2
а + – –
b – + –
с – – +
abc + + +
Заметим, что для построения плана 23-1 выбраны только те комбинации обработок, у которых в столбце «Эффект ABC» стоит плюс. Поэтому ABC называется генератором полуреплики данного вида. Далее, в столбце I также всегда стоят плюсы, и мы называем равенство I = ABC определяющим соотношением для рассматриваемого плана.
Таблица 6 Алгебраические знаки для факторного плана 23
| Комбинация обработок | Факторный эффект | |||||||
| I | A | B | C | AB | AC | BC | ABC | |
| a b c abc ab ac bc (I) | + + + + + + + + | + – – + + + – – | – + – + + – + – | – – + + – + + – | – – + + + – – + | – + – + – + – + | + – – + – – + + | + + + + – – – – |
Комбинациям обработок плана 23-1 соответствуют три степени свободы, которыми можно воспользоваться для оценивания главных эффектов. С помощью таблицы 6 получаем:
A = 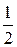 [a – b – c + abc];
[a – b – c + abc];
B = 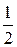 [– a + b – c + abc];
[– a + b – c + abc];
C = 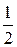 [– a – b + c + abc];
[– a – b + c + abc];
Нетрудно также проверить, что оценки двухфакторных взаимодействий имеют вид:
ВС = 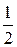 [a – b – c + abc];
[a – b – c + abc];

|
АС = 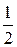 [– a + b – c + abc];
[– a + b – c + abc];
AB = 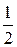 [– a – b + c + abc];
[– a – b + c + abc];
Таким образом, невозможно различить А и ВС, В и АС, С и АВ. В сущности, как можно показать, оценивая А, В и С, мы на самом деле оцениваем А + ВС, В + АС и С + АВ. Два или более эффектов, обладающих таким свойством, называются совместными. В нашем примере совместными являются А и ВС, В и АС, С и АВ.
Структура совместных эффектов для рассматриваемого плана легко устанавливается с помощью определяющего соотношения I = АВС: умножив по модулю 2 обе части этого соотношения на какой-либо эффект, получим совместный с ним эффект. В нашем, примере для А совместным является эффект А • I =А • АВС или А = А2ВС = ВС, так как произведение любого эффекта на тождественный элемент 1 равно этому же эффекту. Аналогично для В совместным является эффект В • I = B • ABC или В = АВ2С = АС, а для С это С • I = С • АВС или С = АВС2 = АВ.
Предположим теперь, что мы выбрали другую полуреплику, т. е. комбинации обработок, которым в столбце АВС: таблицы 6 соответствует знак минус. Таким образом, в альтернативную полуреплику входят комбинации обработок
Обозначение 1 Обозначение 2
(I) – – –
аb + + –
aс – + –
bc – + +
Определяющим соотношением для этого плана является I = – ABC. Пары совместных эффектов имеют вид А = – ВС, В = – АС и С = – АВ, т. е. при оценивании А, В и С по этой по-луреплике мы на самом деле оцениваем А – ВС, В – АС и С – АВ. Дробная реплика, связанная с I=+ABC, называется главной дробной репликой (главным блоком).
В общем случае полуреплика плана 2k, содержащая 2k - 1 наблюдений, называется дробным факторным планом типа 2k - 1. Для его построения полный план типа 2k разбивается на два блока, причем определяющим соотношением служит взаимодействие высшего порядка. Каждый блок представляет собой дробный факторный план типа 2k - 1 с определяющими соотношениями I=±АВС..., где знак генератора зависит от выбора дробной реплики. На практике дробная реплика выбирается случайным образом.
План типа 2k - 1 можно построить и другим способом. Сначала записываются комбинации обработок для полногофакторного эксперимента типа 2k - 1, а затем добавляется k - йфактор, уровни которого, обозначаемые знаками плюс и минус, определяются алгебраическим знаком взаимодействия высшего порядка, а именно, АВС...(К – 1). Следовательно, для построения дробного факторного плана 23-1 надо выписать полный факторный план 22 и приравнять фактор С взаимодействию АВ. Альтернативную дробную реплику можно получить, приравняв фактор С взаимодействию (– АВ). Этот метод иллюстрируется таблицей 7.
Таблица 7 Две полуреплики плана 23
| Полный план 22 | 23-1, I = ABC | 23-1, I = – ABC | |||||
| A | B | A | B | C = AB | A | B | C = – AB |
| – + – + | – – + + | – + – + | – – + + | + – – + | – + – + | – – + + | – + + – |
|
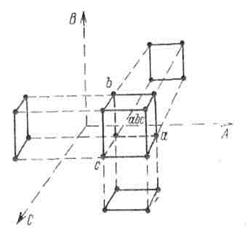
Дробный факторный план типа 2k - 1 можно спроектировать на полныйфакторный план для любых k – 1 из исходных факторов. Для плана 23-1 это очевидно из рассмотрения таблицы 7. На рисунке 4 показано проектирование плана 23-1 с I = ABC на три полных факторных плана 22. Таким образом, если один из факторов оказывается несущественным, то мы можем получить полный факторный план для оставшихся двух факторов. Более того, план типа 2k - 1 можно превратить в две реплики полного факторного плана для любых k – 2 факторов, четыре реплики полного факторного плана для k – 3 факторов и т. д.
Рисунок 4 Проектирование плана 23-1 на три плана 22
|