
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
|
|
Теми практичних занять.
| № з/п | Назва теми | Кількість годин |
| Семестр 1 | ||
Системи лінійних рівнянь. Метод Гаусса
(Основна та розширена матриці СЛР; елементарні перетворення СЛР; метод послідовного виключення змінних: прямий і обернений ходи метода Гауса. Елементи дослідження СЛР: сумісні (визначені, невизначені), несумісні СЛР.)
Кл/з [1] №398, №400-404; [2] №567, 570
Д/з [2] №568, 569, 555; №83, 85
С/р Розв’язати СЛР(3-х рівнянь з 3-ма невідомими)
. 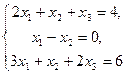 . .
| ||
Бінарні відношення
(Відношення на множинах, прямий добуток множин, бінарне, n -арне відношення; приклади унарних, бінарних, тернарних відношень; область визначення, множина значень; властивості відношень (рефлексивність, антирефлексивність, симетричність, антисиметричність, транзитивність), графіки відношень. Розбиття множини на класи. Фактор-множина. Функціональні відношення, класифікація, їх графіки. Приклади.)
Кл/з [3] №4.2-4.4, №4.16, 4.19а; №4.24; 5.16
Д/з [3] закінчити №4.2-4.4, 4.16, 4.19а; 4.24; 5.16
С/р Доповнити, якщо це можливо, дане відношення ρ ={(1; 2); (2; 3)} 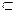 A2, A={1, 2, 3} до 1) рефлексивного; 2) антирефлексивного; 3) симетричного; 4) антисиметричного; 5) транзитивного. A2, A={1, 2, 3} до 1) рефлексивного; 2) антирефлексивного; 3) симетричного; 4) антисиметричного; 5) транзитивного.
| ||
| Алгебраїчні операції. Алгебраїчні структури Алгебраїчні операції, ранг, поняття n -арної операції, заданої на множині А, 0-арні, унарні, бінарні операції, приклади. Види бінарних операцій (комутативність, асоціативність, дистрибутивність відносно іншої бінарної операції), нейтральний та симетричний елементи. Адитивна і мультиплікативна форми запису бінарних операцій. Приклади. Алгебри. Тип алгебри. Однотипні алгебраїчні структури. Аксіоми моноїда, групи, кільця, області цілісності, поля. Приклади. Кл/з [3] №8.1, 8.2, 8.4, 8.7; 8.15; 8.16; 9.2, 9.7; 26.1 Д/з [3] закінчити №8.1; розв’яз. №8.14, 9.1, 9.8 С/рЧи утворює групу множина цілих степенів 5 відносно додавання; множення? | ||
| 4-5 | Поле комплексних чисел
(Запис комплексного числа в алгебраїчній формі, геометрична інтерпретація; дії над комплексними числами в алгебраїчній формі. Спряжені комплексні числа, властивості комплексно спряжених чисел. Геометрична ілюстрація. Тригонометрична форма комплексного числа, дії над комплексними числами в тригонометричній формі: множення, ділення, піднесення до степеня, добування кореня. *Мультиплікативна група коренів з одиниці. *Експоненціальна форма запису комплексного числа.)
Кл/з [3] №10.1(а, г), 10.3; 11.1, 11.10, 11.14(а), 12.1
Д/з [3] №10.1(б, в, д), 10.4; закінч. №11.1, 11.10, 12.1
С/рЗнайти дійсну та уявну частини комплексного числа 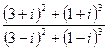 та перетворити в тригонометричну форму число та перетворити в тригонометричну форму число  . .
| |
Дії над матрицями. Перестановки, підстановки
(Матриці та дії над ними. Властивості дій над матрицями. Транспонована матриця. Дії над квадратними матрицями n- го порядку. *Кільце матриць n- гопорядку. Перестановки та підстановки, дії над підстановками (множення та відшукання оберненого), інверсії, inv(α), декремент, парність, непарність підстановки, транспозиція. *Симетрична група всіх підстановок n- го степеня. *Альтернативна група всіх парних підстановок.)
Кл/з [3] №20.1(а, в), 20.3, 20.4(а), 20.9(б), 20.11, 20.14, 21.1(а, в, д), 21.2(б); 18.1(а), 18.2(а), 18.3(б), 18.5, 18.6(а), 18.7(б), 19.1(а)
Д/з [3] №20.1(б, г), 20.4(б), 20.9(а), 21.1(б, г), 21.2(а); 18.1(б), 18.2(б), 18.3(а), 18.4, 18.6(б)
С/р Обчислити добутки 2-х підстановок φ ∙ ψ, ψ ∙ φ, φ -1, обчислити кількість інверсій φ, φ -1, ψ, φ ∙ ψ, ψ ∙ φ. Перемножити 2 матриці розмірів 2х3 та 3х2 або розв’язати матричне рівняння 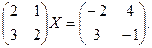
| ||
Визначники n -го порядку, їх властивості та застосування. Формули Крамера
(Рівноправність рядків і стовпців; лінійність та знакозмінність визначника; елементарні перетворення; мінор та алгебраїчне доповнення елемента визначника; розклад визначника за елементами рядка (стовпця). Умови рівності нулю визначника. Способи обчислення визначників. Визначник трикутної матриці. Визначник добутку матриць. Крамерівські СЛР. Взаємно-обернені матриці. Критерій оборотності. Способи знаходження оберненої матриці. Матричний спосіб розв’язування крамерівських СЛР. Приклади.)
Кл/з [3] №21.6(а, б), 21.12(а), 22.1, 22.6(б), 22.7(б), 22.8(в, г), 22.11, 23.6, 24.3(а, г), 20.19, 24.1(а), 19.2(а)
Д/з [3] №22.6(а), 22.7(а), 22.8(а, б), 23.6(а, г), 24.3(б, в), 24.1(е)
С/рРозв’язати систему матричним способом  або знайти коефіцієнт числа а у визначнику: або знайти коефіцієнт числа а у визначнику:  або дослідити і розв’язати систему за теоремою Крамера: або дослідити і розв’язати систему за теоремою Крамера:  або визначити, чи має матриця або визначити, чи має матриця  обернену і, якщо так, то знайти її: обернену і, якщо так, то знайти її: 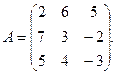
| ||
Контрольна робота
1. Дослідити і розв’язати СЛР методом Гаусса (знайти загальний розв’язок системи 3-х рівнянь з 4-ма невідомими): 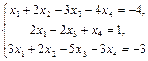 2. Обчислити визначник 3-го порядку 3-ма способами (за означенням, зведенням до трикутного вигляду, за елементами рядка або стовпця) або розв’язати СЛР (3-х рівнянь з 3-ма невідомими) за формулами Крамера.
2. Обчислити визначник 3-го порядку 3-ма способами (за означенням, зведенням до трикутного вигляду, за елементами рядка або стовпця) або розв’язати СЛР (3-х рівнянь з 3-ма невідомими) за формулами Крамера. 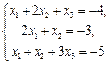 3. Добути корені 4-го степеня із комплексного числа виду а+b∙ і:
3. Добути корені 4-го степеня із комплексного числа виду а+b∙ і:  ; ; 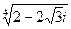 ; ; 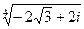 4. Перевірити, чи утворює групу деяка множина відносно заданих операцій.
4. Перевірити, чи утворює групу деяка множина відносно заданих операцій.
| ||
| Усього годин за 1 семестр | ||
| Семестр ІІ | ||
Арифметичний векторний простір
(Арифметичний n -вимірний лінійний простір, означення, властивості, арифметичні вектори та властивості дій над ними, лінійна залежність і незалежність системи векторів, їх властивості. Еквівалентні системи векторів. Приклади.)
Кл/з [3] №29.5(а-д), 30.8, 30.5, 32.2, перевірити за означенням: чи є система векторів ЛЗ
Д/з[3] №29.5(є-к), 32.2; 1 приклад – перевірити за означенням: чи є система векторів ЛЗ
С/р Перевірити, чи утворює множина векторів 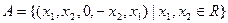 лінійний (векторний) простір і знайти його розмірність і базис. лінійний (векторний) простір і знайти його розмірність і базис.
| ||
Ранг матриці. Дослідження СЛР
(Ранг матриці, способи обчислення, приклади, рівність рядкового і стовпцевого рангів матриці; мінорний ранг матриці. Основна і розширена матриці СЛР, теорема Кронекера-Капеллi (критерій сумісності СЛР та критерій визначеності сумісної СЛР).)
Кл/з [3] №22.9, 17.1(а, б), 17.9(а, в), 17.10
Д/з [3] №22.9(зак.), 17.1(в), 17.9(б, г)
С/р Розв’язати, спочатку дослідивши її за критеріями сумісності та визначеності. 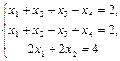
| ||
Підпростори. Критерій підпростору
Лінійний (векторний) простір, система твірних, базис простору, розмірність лінійного простору. Поняття підпростору, приклади підпросторів арифметичного n -вимірного простору; критерій підпростору. Лінійна оболонка системи векторів. Загальний прийом отримання підпростору простору V.
Кл/з [3] №29.1, 29.2, 29.5(а, б), 29.4; 29.3′
Д/з [3] №29.3, 29.5(в-к)
С/р Перевірити, чи утворює множина векторів  лінійний простір і, якщо так, то знайти його розмірність і базис. лінійний простір і, якщо так, то знайти його розмірність і базис.
| ||
Перетин, сума і пряма сума підпросторів.
Підпростір, перетин, сума, пряма сума підпросторів, їх означення, властивості, розмірність перетину, суми, прямої суми. Об’єднання підпросторів, означення, властивості (не завжди є простором!); доповнення підпростору U до простору V. Лінійна оболонка Приклади.
Кл/з [3] №32.3, 32.2(а, в), 32.5(а, г), 32.6(а-в)
Д/з [3] №32.2(б, г), 32.5(б, д), 32.6(г)
С/р Побудувати перетин та суму підпросторів U=L(a1, a2), V= L(b1, b2), що є лінійними оболонками, натягнутими на системи векторів a1=(1, -1, 2), a2=(1, 2, 1), b1=(2, 1, 3), b2=(1, 1, 1) та визначити розмірності U 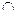 V, U+ V. V, U+ V.
| ||
Лінійна оболонка системи векторів. Лінійний многовид. ОСЛР та НОСЛР
Поняття лінійної комбінації, лінійної оболонки системи векторів. Розмірність лінійної оболонки, що натягнута на дану систему векторів. Приклади скінченновимірних та нескінченновимірних векторних просторів. Поняття лінійного многовиду. Твердження про множину усіх розв’язків однорідної СЛР (утворює простір, базис якого – ФСР, dim L= n-r) та множину розв’язків НОСЛР (утворює лінійний многовид 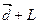 ).
Кл/з [3] №32.10, 32.11; базисна задача №1 §33; 33.1
Д/з [3] №32.11(б, в), 33.1(б, в)
С/р Вказати базис і розмірність лінійної оболонки, що натягнута на систему векторів: ).
Кл/з [3] №32.10, 32.11; базисна задача №1 §33; 33.1
Д/з [3] №32.11(б, в), 33.1(б, в)
С/р Вказати базис і розмірність лінійної оболонки, що натягнута на систему векторів: 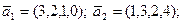 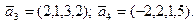
| ||
Координати вектора в різних базисах
Поняття координат вектора; поняття базису векторного простору, скільки існує базисів векторного простору, скільки векторів вони налічують (одн. число). Матриця переходу Т від одного базису до іншого. Зв’язок між координатами вектора в різних базисах.
Кл/з [1] №881 (а), 882(б)
Д/з [1] №881(б), 882(а)
С/р На площині дано два вектори  і і 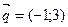 . Обґрунтуйте, що вони утворюють базис і знайдіть розклад вектора . Обґрунтуйте, що вони утворюють базис і знайдіть розклад вектора 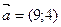 за цим базисом. за цим базисом.
| ||
| 7-8 | Евклідів та унітарний простори
Скалярне множення, евклідів векторний простір. Ортогональні системи векторів, властивості, ортогональний базис простору. Процес ортогоналізації. (Rn, +, ω λ ) з стандартним скалярним добутком – евклідів. Ортонормовані базиси. Ізоморфізм просторів. Ортогональне доповнення. Унітарні простори
Кл/з [3] № 34.2, 34.3(а, в), 34.4(а, г), 34.5(в), 34.6(а); 35.3(б); 34.7(а) або [2] № 1357-1363
Д/з [3] № 34.3(б, в, д), 34.4(в, д), 34.5(б), 34.6(б) та [1] № 899-903
С/р Ортогоналізувати, якщо це можливо, систему векторів:  або Побудувати ортогональний базис простору, що є лінійною оболонкою, натягнутою на систему векторів: або Побудувати ортогональний базис простору, що є лінійною оболонкою, натягнутою на систему векторів: 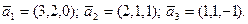
| |
Лінійні оператори. Матриця ЛО
Лінійний (векторний) простір, гомоморфізм (ізоморфізм) векторних просторів. Лінійний оператор, приклади (оператор гомотетії, оператор проектування, оператор диференціювання). Матриця ЛО.
Кл/з [3] №36.2(б, в), 36.6(а), 36.5(а), 36.10(а) або [2] № 1441-1444, 1446, 1451-1452
Д/з [3] №36.2(а, г, д), 36.6(б), 36.5(б)
С/р З’ясувати, чи є оператор  , заданий координатами, як функція координат вектора , заданий координатами, як функція координат вектора 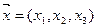 , лінійним. У випадку лінійності знайти його матрицю: , лінійним. У випадку лінійності знайти його матрицю: 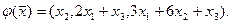
| ||
| Перетворення координат під дією ЛО. Матриці ЛО в різних базисах Зв’язок між матрицями вектора-образа та вектора-прообраза: М(φ (х))=М(φ)∙ М(х), між матрицями ЛО в різних базисах М′ (φ)=Т-1∙ М(φ)∙ Т, матриця переходу від одного базису до іншого. Приклади обчислень. Подібні матриці. Кл/з [3] №36.11(а, б), 37.1(а, в), 37.2(а, б), 37.3(а, б) або [2] №1453, 1454 Д/з [3] №36.11(в), 37.1(б), 37.2(в), 37.3(в) | ||
| 11-12 | Операції над ЛО. Структура лінійного відображення
Означення суми, добутку двох операторів, добутку оператора на скаляр, оберненого оператора. Теореми про те, що φ +ψ, λ φ, φ ψ, φ -1 – ЛО, їхні матриці. Ядро ЛО: означення, теорема: (Ker φ, +, ω λ ) – векторний простір, дефект ЛО. Образ ЛО: означення, теорема: (Іт φ, +, ω λ ) – векторний простір, ранг ЛО.
Кл/з [3] № 38.2(а), 38.3, 39.2; або [2] № 1457, 1459, 1461; [3] базисна задача 1 § 39 (вектор-стовпці, а не рядки!), 39.1 (І ст.)
Д/з [3] № 38.2(б), 38.3(б, г), №39.1 (ІІ ст.)
С/р ЛО φ задано матрицею 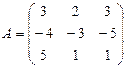 . Побудувати Kerφ та Іт φ, встановити їх розмірності. . Побудувати Kerφ та Іт φ, встановити їх розмірності.
| |
| 13-14 | Власні значення і власні вектори ЛО.
Власні вектори, власні значення ЛО, приклади. ЛО з простим спектром. Алгоритм відшукання власних значень і власних векторів ЛО. Умови, за яких матриці ЛО зводяться до діагонального вигляду. *Спряжені та самоспряжені оператори. Унітарні ЛО. (*[3] базисна задача 2 § 41, 41.12-без дов., 41.13)
Кл/з [3] базисна задача 1 § 40, №40.1(І ст.); базисна задача 1 § 41(А1, А2), 41.1(а, б, д) або [1] 925
Д/з [3] №40.1(ІІ ст.), 41.1(в, г, е)
С/р Чи зводиться матриця лінійного оператора  до діагональної за допомогою переходу до нового базису. Знайти цей базис і відповідну діагональну матрицю, якщо до діагональної за допомогою переходу до нового базису. Знайти цей базис і відповідну діагональну матрицю, якщо 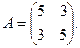 або Знайти власні вектори та власні значення лінійного оператора j, заданого матрицею або Знайти власні вектори та власні значення лінійного оператора j, заданого матрицею 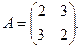
| |
| 15-16 | Квадратичні форми Квадратичні форми, ранг, індекс КФ, дійсні КФ. Додатньо означені КФ, критерій Сильвестра. Зведення КФ до діагонального вигляду: метод Лагранжа, метод ортогональних перетворень (власні вектори і власні значення), зведення до головних осей. Кл/з [1] №939(a, с, d), 951(а-f) + матриці перетворень Д/з [3] №939(в, е), 951(g-k) + матриці перетворень С/р Використовуючи метод Лагранжа, встановити тип поверхні 2-го порядку x12+2∙ x1x2+4x1x3– x32=1. | |
Контрольна робота
1. Ортогоналізувати систему векторів (3 вектори з R4, R5).
2. Знайти матрицю ЛО у новому базисі (φ: R3→ R3).
3. Знайти власні вектори і власні значення ЛО
(φ: R3→ R3).
4. Звести КФ (А(х, х), х 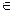 R3) до канонічного вигляду методом Лагранжа. R3) до канонічного вигляду методом Лагранжа.
| ||
| Усього годин за 2 семестр | ||
| Усього годин |
Данная страница нарушает авторские права?