
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теорема.
|
|
Крива у = f (x) тоді і тільки тоді має асимптоту y = kx + b, коли існують скінченні границі 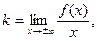
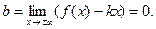
3. Горизонтальні асимптоти. Якщо в похилій асимптоті у = kх + b функції у = f(x) маємо k = 0, то таку похилу асимптоту називають горизонтальною асимптотою функції: у = b.
Для того, щоб пряма у = b була горизонтальною асимптотою функції y = f(x), необхідно і достатньо, щоб існувала скінченна границя 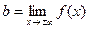 .
.
Загальна схема дослідження функції y = f(x)
Перший етап (використання властивостей заданої функції)
| 1. Область визначення функції y = f(x) | D(f) |
| 2. Парність, непарність і періодичність | f(x)- парна, якщо
 D(f) – симетрична відносно осі Оу;
f(-x) = f(x);
f(x)- непарна, якщо D(f) – симетрична відносно осі Оу;
f(-x) = f(x);
f(x)- непарна, якщо
 D(f) – симетрична відносно початку координат;
f(-x) = - f(x);
f(x)- періодична, якщо f(x+Т) = f(x) D(f) – симетрична відносно початку координат;
f(-x) = - f(x);
f(x)- періодична, якщо f(x+Т) = f(x)
|
| 3. Точки перетину графіка з осями координат | а) з віссю Ох: з рівняння f(x) = 0 знаходять х; б) з віссю Оу: x = 0, знаходять значення у = f(0) |
| 4. Точки розриву. Асимптоти графіка функції у = f(х) | Вертикальні асимптоти – у точках нескінченного розриву 2-го роду функції у = f(х)
Похилі асимптоти: y = kx + b,

|
Другий етап (використання похідної першого порядку)
| 5. Знайти похідну та критичні точки функції у = f(х) | f’(х) f’(х)= 0або f’(х) не існує |
| 6. Проміжки зростання, спадання | f’(х)> 0 – зростає, f’(х)< 0 - спадає |
| 7. Точки екстремуму функції у = f(х) | Якщо f’(х) змінюєзнак при переході через х 0 з «+» на «-», то х 0 = х max, з «-» на «+», то х 0 = х min |
Третій етап (використання похідної другого порядку)
| 8. Знайти другу похідну та критичні точки другого роду | f’’(х) f’’(х)= 0або f’’(х) не існує |
| 9. Проміжки опуклості, угнутості | f’’(х)< 0 – функція угнута; f’’(х)> 0 – опукла |
| 10. Точки перегину і значення функції в цих точках | Якщо f’’(х) змінюєзнак при переході через х 0, то х 0 – точка перегину |