Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные технические характеристики шайб шпоночного типа
|
|
| Тип шайб (шпонок) | Разм Диаметр,
| еры шайб, Высота,

| им Тол щи-на,

| Площадь ослабления | Диаметр болта, мм | Наименьшие размены сечений соединяемых элементов, см | Наименьшее расстояние между шайбами по осям, см | Несущая пособносп шайбы, кН |
| Когтевая Лен-нова | 80 100 120 150 | 15, 3 18, 7 22 27 | 2 2 2 2, 5 | 8 12 18 28 | 20 20 24 24 | 5x10 6x13 7, 5x15 9x18 | 20 24 30 | 9, 6 15 21, 6 33, 8 |
| Двустронняя и односторонняя (для присоединения металлических пластин) системы " Аппель" | 65 80 95 126 | 30 30 30 30 45 | 5 6 6 6 | 7, 8 10, 1 12, 3 17 25, 9 | 12 12 12 12 12 | 4x10 5x11 6x12 6x16 6x20 | 14 18 22 25 30 | 11, 5 14 17 20 28 |
| Тарельчатые системы " Хри-стофа и Унма-ка" | 60 80 100 120_, | 20 25 30 | 4, 5 5 5 5 | 4, 7 8, 4 13, 1 18, 8 | 12 12 12 12 | 4x10 5x11 6x13 6x16 | 21 24 27 | 12, 5 16, 0 20, 0 23, 0 |
| Двусторонняя зубчато-кольцевая системы " Фреерс и Нильсон" | 90 130 155 | 30 40 45 | 6, 5 8 10 | 9, 7 19, 8 27, 6 | 12 12 16 | 6x14 8x20 10x20 | 20 25 32 | 14, 5 22, 0 31, 5 |
| Двусторонняя системы Котова | 120 140 160 180 200 220 | 30 30 30 30 30 30 | 3 3 3 3 3 3 | 18 021 24 27 30 33 | 20 22 27 27 30 30 | 6x15 6x18 6x20 7, 5x22 7, 5x24 8x26 | 24 28 32 36 40 44 | 18 21 24 27 30 33 |
| Двусторонняя системы " Гека" | 50 65 80 95 115 | 27 27 27 27 27, | 3 3 3 3 | 2, 8 3, 6 4, 6 5, 6 7 | 12 16 20 24 32 | 4x10 4x11 5x13 6x14 6x17 | 12 14 17 20 23 | 8 11, 5 17 21 |
| Односторонняя системы " Гека" | 50 65 80 95 115 | 15 15 15 15 15 | 3, 4 4, 5 5, 5 6, 9 8, 6 | 3 3 3 3 3 | 12 16 20 22 24 | 4x10 4x11 5x13 6x14 6x17 | 12 14 17 20 23 | 8 11, 5 17 21 27 |
| системы " Аллигатор" | 70 95 115 125 | 19 24 24 29 | 1, 45 1, 5 1, 5 1, 65 | 2, 6 4, 5 5, 6 7, 3 | 16 20 22 24 | 5x12 6x14 8x18 8x19 | 14 17 20 23 | 8 12 16 18 |

Рис. 3.14. Схема работы нагеля: а - первоначальное положение; б - поворот; в -и-формированный нагель; г - эпюры сминающих упругопластичных напряжений (ревесины; Товар - сдвигающее усилие; Т1, Т2 - равнодействующие сминающих напряжений древесины
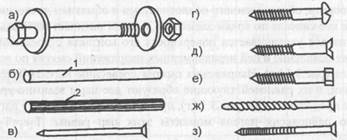
Рис. 3.15. Основные виды циклических нагелей: а - болт с гайкой и круглыми (могут быть также квадратными) шайбами; б - цилиндрический нагель из стали (1), из твердых пород древесины или стеклопластика (2); в - гвоздь; г - шуруп с полузакругленной головкой; е - глухарь; ж, з - особые виды гвоздей с профильной поверхностью
Цилиндрические нагели и болты применяют для сплачивания элементов деревянных конструкций, соединения их по длине (рисЗ. 16, а), а также в узловых примыканиях (рис.3.16, в). Соединения деревянных элементов на нагелях бывают симметричными и несимметричными.
На плотность соединений на нагелях значительно влияет совпадение отверстий под нагели в соединяемых элементах. Чтобы получить хорошее совпадение отверстий и достичь максимальной плотности соединения, необходимо сверлить отверстия в предварительно собранном и обжатом пакете. Для обжатия соединений ставят стяжные болты в количестве 25% общего числа нагелей. Если стяжные болты сделаны из того же материала, что и нагели, то их включают в расчетное количество нагелей.
В растянутых стыках по ширине элемента следует ставить только четное количество продольных рядов нагелей. Это требование объясняется тем, что при нечетном числе рядов средний оказывается по оси доски в зоне наиболее возможного появления продольных трещин в результате усушки дерева.
По аналогии с соединениями на заклепках в металлических конструкциях, каждое пересечение нагеля с рабочим швом называется «срезом». Однако при общности действующих явлений в том и в другом случае работа нагеля в соединениях элементов значительно отличается от работы заклепки в металлических элементах. Заклепка соединяет тонкие стальные элементы. Отношение длины заклепки к ее диаметру невелико, что характеризует большую относительную жесткость, при которой изгибные напряжения не имеют существенного значения и могут не учитываться. Несущую способность заклепки определяют из расчета на смятие и срез.
В соединениях деревянных элементов отношение длины нагеля к его диаметру значительно больше, поэтому нагель работает как гибкий стержень главным образом на изгиб и неравномерно сминает древесину в гнезде. Напряжения среза в нагеле не учитываются в расчете, поскольку срезать деревянным элементом нагель, даже деревянный, не говоря уже о стальном, нельзя. Термин «срез» употребляется для характеристики соединения по количеству плоскостей относительного сдвига между соединяемыми элементами, которые пересекаются нагелями. В зависимости от расположения срезов по отношению к осям действия сил различают симметричные и несимметричные соединения (рис. 3.17). Расчет нагельных соединений основан на том положении, что действующее на соединение (связь) усилие не должно превышать расчетной несущей способности соединения (связи) Т. Расчетное количество нагелей принимают не менее двух с диаметром 12-24 мм и определяют по формуле

где N - расчетное усилие, действующее в растянутом стыке, 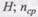 - количество срезов нагеля; Тн - наименьшая расчетная несущая способность одного среза нагеля,
- количество срезов нагеля; Тн - наименьшая расчетная несущая способность одного среза нагеля, 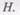

Рис. 3.16. Узловые соединения на цилиндрических нагелях: а - с прямой расстановкой; б - с круговой расстановкой
Рис. 3.17. Соединения на цилиндрических нагелях деревянных растянутых элементов:
а - симметричное двухсрезное;
б - несимметричное односрезное
Для сплачивания двух или трех брусьев, составленных по высоте, применяют пластинчатые нагели, вставляемые в гнезда, прорезанные цепнодолбежным станком (рис.3.18).
Применение дубовых или березовых пластинчатых нагелей допускается для сплачивания брусьев в составных элементах со строительным подъемом, работающих на поперечный изгиб и на сжатие с изгибом. Размеры пластинчатых нагелей и гнезд для них, а также расстановку пластинчатых нагелей в сплачиваемых элементах следует принимать по нормам /21 (см. рис.3.18). Направление волокон в пластинках должно быть перпендикулярно плоскости сплачивания деревянных элементов.
Расчетную несущую способность дубового или березового пластинчатого нагеля [кН] с размерами, даваемыми СНиП 11-25-80 в соединяемых элементах из древесины сосны и ели, следует определять по формуле
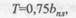
где 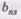 - ширина пластинчатого нагеля, см., которую следует брать равной ширине сплачиваемых элементов
- ширина пластинчатого нагеля, см., которую следует брать равной ширине сплачиваемых элементов  при сквозных пластинах,
при сквозных пластинах, 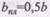 - при глухих.
- при глухих.
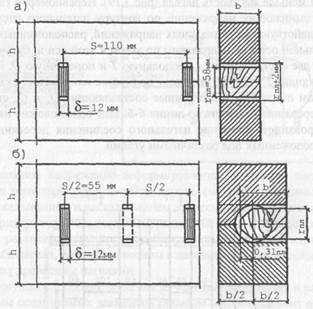
Рис. 3.18. Соединения на пластичных нагелях: а - со сквозными пластинками; б - с глухими пластинками
При применении для сплачивания элементов из других пород древесины следует вводить поправочный коэффициент тп (табл. 11.2 Приложения II или табл.4 СНиП П-25-80).
Для конструкций, эксплуатируемых в условиях повышенной влажности или температуры и рассчитываемых на действие кратковременных или постоянной и длительной временной нагрузок, расчетную несущую способность пластинчатых нагелей следует умножать на поправочные коэффициенты  (табл. 11.5 и 11.6 Приложения II или табл. 5 и 6 СНиП П-25-80).
(табл. 11.5 и 11.6 Приложения II или табл. 5 и 6 СНиП П-25-80).
3.3.3 Определение расчетной несущей способности одного «среза» нагеля
Для определения несущей способности одного среза нагеля следует рассмотреть напряженное состояние нагельного соединения. Действующие в соединяемых элементах усилия стремятся сдвинуть их относительно друг друга. Нагель, препятствуя этому, изгибается. Изгиб нагеля зависит от жесткости самого нагеля и смятия древесины нагельного гнезда. Нагель можно рассматривать как балку, лежащую на сплошном упругопластическом основании - древесине нагельного гнезда. Напряжения смятия в древесине по длине нагеля распределены неравномерно. Эта неравномерность тем значительнее, чем меньше жесткость нагеля (рис.3.19). Неравномерно также распределение сминающих напряжений по контуру нагельного гнезда (рис. 3.20).
 Равнодействующие радиальных напряжений, расположенных выше и ниже продольной оси х-х, направлены по углом к этой оси и, будучи разложены, дают две составляющие - продольную Т и поперечную
Равнодействующие радиальных напряжений, расположенных выше и ниже продольной оси х-х, направлены по углом к этой оси и, будучи разложены, дают две составляющие - продольную Т и поперечную 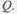 Продольная составляющая Т = Тн+ Тв вызывает появление напряжений скалывания по площадкам а-а и а'-а'. Поперечные составляющие
Продольная составляющая Т = Тн+ Тв вызывает появление напряжений скалывания по площадкам а-а и а'-а'. Поперечные составляющие
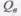 и стремятся расколоть деревянный элемент по линии б-б. Еще более сложно напряженно-деформированное состояние нагельного соединения деревянных элементов, расположенных под различными углами.
и стремятся расколоть деревянный элемент по линии б-б. Еще более сложно напряженно-деформированное состояние нагельного соединения деревянных элементов, расположенных под различными углами.
Несущая способность нагеля из условий скалывания и раскалывания древесины соединяемых элементов главным образом зависит от расстановки нагелей. Минимальное расстояние между нагелями назначают таким образом, чтобы в соединении несущая способность соединяемых деревянных элементов по скалыванию и раскалыванию заведомо превышала несущую способность нагеля по его изгибу и смятию древесины нагельного гнезда.

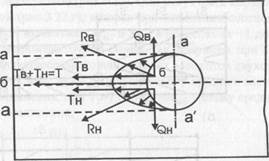
Рис 3.20. Эпюры радиальных напряжений смятия древесины нагельного гнезда
Рис. 3.19. Эпюры напряжений древесины нагельного гнезда смятия и изгибающих
моментов в нагеле: а - при диаметре нагеля 25 мм; б - то же, 12 мм
Несущая способность нагеля из условий скалывания и раскалывания древесины соединяемых элементов главным образом зависит от расстановки нагелей. Минимальное расстояние между нагелями назначают таким образом, чтобы в соединении несущая способность соединяемых деревянных элементов по скалыванию и раскалыванию заведомо превышала несущую способность нагеля по его изгибу и смятию древесины нагельного гнезда.
Минимальные расстояния между осями нагелей принято выражать в диаметрах нагеля. Они определяются видом нагелей и толщиной соединяемых элементов. Расстановка нагелей в соединениях может быть прямой или в шахматном порядке (рис.3.21). В табл. 3.4 приведены рекомендуемые СНиП П-25-80 121 минимальные расстояния между цилиндрическими нагелями.
Таблица 3.4.
Минимальные расстояния между нагелями


Рис. 3.21. Расстановка нагелей: а - прямая; б - в шахматном порядке
При соблюдении расстановки нагелей расчетная несущая способность одного нагеля Тн определяется только из условий изгиба нагеля и смятия древесины нагельного гнезда в обоих прилегающих к шву элементах. Теоретически нагель, как уже указывалось, рассматривают как балку, лежащую на упругом или упругопластическом основании, за которое принимают древесину соединяемых элементов. В основу расчета могут быть положены различные теоретические предпосылки, характеризующие само основание, режимы нагружения, особенности деформирования во времени и другие факторы. Однако расчет нагеля сложнее, чем расчет балки, лежащей на сплошном основании. Сложность задачи состоит в следующем:
основание, на которое опирается нагель, разделено на части, например, в симметричном двухсрезном соединении имеются две крайние и одна средняя часть;
действующее усилие приложено к деревянным элементам соединения и передается на нагель в виде напряжений смятия нагельного гнезда;
эпюра давления по длине нагеля неравномерна и зависит от толщины элементов и диаметра нагеля.
Другим, более удобным для инженерных расчетов методом определения несущей способности нагеля является экспериментально-теоретический метод. В этом случае эпюры напряжений смятия задают по толщине элементов. Нагель также рассматривают в виде стержня, работающего в упругопластической среде, а соединения расчленяются на три основные схемы: для несимметричной односрезной, схемы для кососимметричной двух срезной и симметричной двухсрезной (рис.3.22). Они могут быть выражены одной обобщенной схемой (рис.3.22, г), которая при изменении соотношений между силами Т1 и Т2 и моментами Мш1 и Мш2 в пределах от +1 до -1 охватывает все основные и промежуточные схемы. Так, например, при Т1+0 и Мш1+0 получим схему для односрезного или крайних элементов двухсрез-ных соединений; при Т}— -Т2 и Мш1= -Мш2 получим схему среднего элемента кососимметричного соединения; при Т1=Т2 и Мш1=Мш2 - схему среднего шемента симметричного соединения.
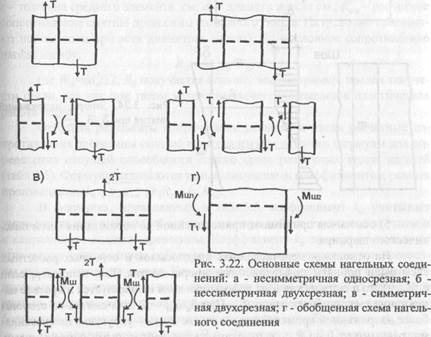
При разработке этого метода (автор - д-р техн.наук В.М.Коченов) для упрощения расчета были введены следующие предпосылки:
1) принята диаграмма деформирования идеального упругопластичного материала (рис.3.23) для смятия древесины и для изгиба нагеля;
2) в пределах пластического участка напряжения остаются постоянными, равными для древесины расчетному сопротивлению смятию, и для нагеля расчетному сопротивлению изгибу, что для стали приравнивается пределу текучести;
3) несущую способность нагеля определяют не разрушением соединения, а расчетной предельной деформацией;
4) расчетную предельную деформацию ограничивают отношением полной деформации к упругой (рис. 3.24), которое принимают