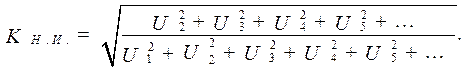Линейные электрические цепи с несинусоидальными токами и напряжениями

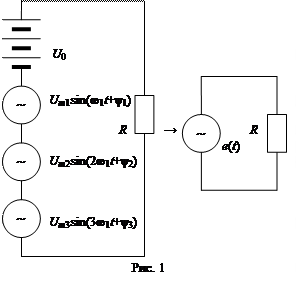
Если несколько источников напряжения с разными частотами 0, ω ₁, 2ω ₁, 3ω ₁, амплитудами U_{m 1}, U_{m 2}, U_{m 3} и начальными фазами ψ ₁, ψ ₂, ψ ₃ присоединить последовательно к линейной цепи R, то напряжение и ток в этой цепи окажутся несинусоидальными. Можно также считать, что на цепь воздействует только одна несинусоидальная периодическая ЭДС. e (t), которую можно представить в виде ряда

e (t)= U ₀+ U_{m 1}sin(ω ₁ t +ψ ₁)+ U_{m 2}sin(2ω ₁ t +ψ ₂)+ U_{m 3}sin(3ω ₁ t +ψ ₃).

Первый член ряда U ₀ называют постоянной составляющей или нулевой гармоникой. Второй член ряда U_{m 1}sin(ω ₁ t +ψ ₁) называют первой или основной гармоникой. Остальные члены ряда называют высшими гармониками, например, наименования второго и третьего членов, а также их параметров следующие:

U_{m 2}sin(2ω ₁ t +ψ ₂) – вторая гармоника;

U_{m 3}sin(3ω ₁ t +ψ ₃) – третья гармоника;

где ω ₁=2π / T – основная частота, T – период несинусоидального периодического колебания; U_{m 1}, U_{m 2}, U_{m 3} – амплитуды гармоник, ψ ₁, ψ ₂, ψ ₃ – начальные фазы гармоник.

Все сигналы, отличные от гармонических, называют негармоническими.

Из курса математики известно, что всякая периодическая функция, удовлетворяющая условиям Дирихле, т.е. ограниченная, имеющая за полный период конечное число разрывов первого рода и конечное число максимумов и минимумов, может быть разложена в тригонометричес-кий ряд Фурье. Пусть переменная x связана с временем t соотношением x= ω t= 2 π t / T,

где Т – период функции во времени, при этом период функции по x равен 2π.

Периодический сигнал x (t) может быть представлен:

1) – одинарным рядом Фурье, когда:

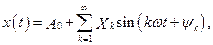
где k – номер гармоники (k =0, 1, 2, 3, …), Х_k – амплитуда гармоники с номером k, ψ _k – начальная фаза гармоники с номером k;

2) – двойным рядом Фурье, когда:

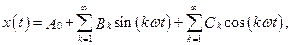
где A ₀ – постоянная составляющая (нулевая гармоника); B_k, C_k – коэффициенты ряда k =1, 2, 3, …

Для определения этих коэффициентов используются формулы:

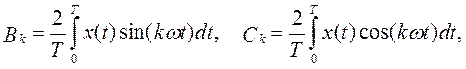
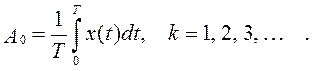
Коэффициенты одинарного ряда находятся через коэффициенты двойного ряда:

Разложение в ряд Фурье не является математической абстракцией. В реальных электрических цепях при несинусоидальных токах или напряжениях эти гармоники реально существуют и могут быть выделены с помощью резонансных цепей. Встречающиеся в электротехнике периодические кривые можно подразделить на две группы:

1) – кривые произвольной (геометрически неправильной формы), обычно задаваемые в виде графика; разложение их в ряд Фурье производят графоаналитическим методом;

2) – кривые геометрически правильной формы (например, трапецеидальной, треугольной, прямоугольной и др.), разложение некоторых из них в ряд Фурье приведено в таблице 1.

Для анализа большинства цепей с несинусоидальными токами достаточно знать величину постоянной составляющей и нескольких первых гармоник ряда, которые можно регистрировать с помощью анализатора спектра.

Обычные измерительные приборы в силу своей инерционности могут измерять только усредненные значения переменных токов и напряжений. Так, приборы магнитоэлектрической системы показывают величину постоянной составляющей, например, напряжения 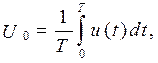где Т =2π /ω – период несинусоидального напряжения. Приборы электромагнитной, электродинамической и тепловой системы показывают действующее (среднеквадратичное) значение измеряемой величины:

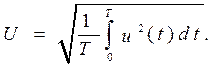
Несинусоидальный сигнал принято также характеризовать с помощью коэффициента нелинейных искажений (коэффициента гармоник), который в общем случае определяют как