Измерение неравенства доходов

Рассмотрим методы расчета двух основных измерителей неравенства доходов: коэффициента фондов и коэффициента Джини.

Коэффициент фондов. Для расчета этого показателя исследуемые домохозяйства располагают по возрастанию дохода, а затем разбивают на несколько равночисленных групп. Первую группу называют " беднейшей", а последнюю - " богатейшей". Коэффициент фондов определяют как отношение среднего дохода в богатейшей группе к среднему доходу в беднейшей группе. Коэффициент фондов также можно определить как отношение суммарного дохода богатейшей группы к суммарному доходу беднейшей группы. Приведенные определения эквивалентны, причем из них следует, что коэффициент фондов составляет не меньше единицы. В случае абсолютного равенства, когда доходы всех домохозяйств одинаковы, данный показатель принимает свое минимальное значение, равное единице.

На практике наиболее часто используют три частных коэффициента фондов: децильный, квинтильный и квартальный:

· децильный коэффициент ( от лат. deci - десятая часть) равен отношению среднего дохода 10% богатейших домохозяйств к среднему доходу 10% беднейших домохозяйств. Данный коэффициент является разновидностью коэффициента фондов, он отвечает случаю, когда множество всех домохозяйств разбивают на десять групп;

· квинтильный коэффициент ( от лат. quinta - пятая часть) равен отношению среднего дохода 20% богатейших домохозяйств к среднему доходу 20% беднейших домохозяйств. Данный коэффициент отвечает случаю, когда множество всех домохозяйств разбивают на пять групп;

· квартильный коэффициент ( от лат. quarta - четвертая часть) равен отношению среднего дохода 25% богатейших домашних хозяйств к среднему доходу 25% беднейших домохозяйств. В данном случае все домохозяйства разбиваются на четыре группы.

Децильный коэффициент больше квинтильного коэффициента, поскольку средний доход 10% богатейших домохозяйств больше среднего дохода 20% богатейших, а средний доход 10% беднейших домохозяйств меньше среднего дохода 20% беднейших. Таким образом, в формуле расчета децильного коэффициента числитель больше, а знаменатель меньше, чем в формуле расчета квинтильного коэффициента. Аналогичным образом можно доказать, что квинтильный коэффициент больше квартильного.

Пример 1. Рассматриваются десять домохозяйств, доходы которых составляют арифметическую прогрессию: 301, 302,., 309, 310. Тогда децильный коэффициент равен 310: 301 = 1, 030, а квинтильный коэффициент равен

(309+ 310): (301 +302) = 1, 026.

Недостатком коэффициента фондов является его слабая чувствительность к изменениям доходов домохозяйств. Так, данный коэффициент не изменит своего значения в случае, когда:

· доход домохозяйства из богатейшей группы увеличится;

· доход домохозяйства из беднейшей группы уменьшится;

· доход домохозяйства, не относящегося к двум крайним группам, изменится в пределах от максимального дохода в беднейшей группе до минимального дохода в богатейшей группе.

Коэффициент Джини, или индекс концентрации доходов. Для расчета этого показателя исследуемые домохозяйства располагают по возрастанию дохода, а затем разбивают эту последовательность на несколько равночисленных групп, как и в методе расчета коэффициента фондов. Однако здесь число этих групп обычно значительно больше десяти. В предельном случае оно совпадает с числом домохозяйств, так что каждое домохозяйство представляет собой отдельную группу. Именно этот случай принят нами за основу при описании алгоритма расчета коэффициента Джини.

Рассмотрим группы домохозяйств, состоящие из одного, двух, трех и т.д. беднейших домохозяйств. Если общее число исследуемых домохозяйств равно п, то удельный вес /-й беднейшей группы в общей численности всех домохозяйств составит

a_i = i/n.

Для первой беднейшей группы, состоящей из самого бедного домохозяйства, данный показатель равен 1/n, а для n-й беднейшей группы, состоящей из всех домохозяйств, он равен единице.

Обозначим через b_i удельный вес суммарного дохода домохозяйств i -й беднейшей группы в суммарном доходе всех домохозяйств (выражен десятичной дробью). С увеличением номера беднейшей группы показатель увеличивается, а для n-й беднейшей группы, состоящей из всех домохозяйств, он принимает свое максимальное значение, равное единице. Показатель b_i не превосходит показатель а_i для любой группы. При равномерном распределении дохода эти показатели равны между собой для любой группы.

Кривая Лоренца - это ломаная, которая состоит из отрезков, соединяющих соседние точки (а_i; b_i). Число отрезков, составляющих ломаную, равно числу исследуемых домохозяйств. Если число домохозяйств весьма велико (например, когда исследуется дифференциация доходов в стране), кривая Лоренца принимает форму плавной дугообразной линии (см. рис.7.1, а).

Кривая Лоренца обладает следующими свойствами:

· ее концами служат точки О (0; 0) и А (1; 1);

· она является восходящей кривой, расположенной под биссектрисой первого координатного угла;

· при равном распределении доходов она совпадает с отрезком ОА;

· при абсолютно неравномерном распределении доходов (когда доход всех домохозяйств, кроме одного, равен нулю) она состоит из двух отрезков, один из которых лежит на оси абсцисс. Чем больше число домохозяйств, тем ближе угол между этими отрезками к прямому углу;

· чем больше степень неравенства доходов, тем больше площадь между кривой Лоренца и биссектрисой первого координатного угла ОА. Данное свойство кривой Лоренца позволяет дать геометрическую интерпретацию коэффициента Джини.

Коэффициент Джини - это измеритель неравенства доходов, численно равный удвоенной площади между линией абсолютного равенства (отрезком ОА) и кривой Лоренца (удвоенной площади фигуры S на рис.7.1, а). Из данного определения следует, что возможные значения коэффициента Джини лежат в пределах от нуля до единицы. Данный показатель равен нулю при абсолютном равенстве доходов и близок к единице при абсолютном неравенстве доходов.

Пример 2. Предположим, что ежемесячный доход Ивана равен 6 тыс. руб., Федора - 3 тыс. руб., Глеба - 1 тыс. руб. Найдем коэффициент Джини (см. рис.7.1, б).

Суммарный доход всех трех домохозяйств равен 10 тыс. руб.

Поскольку Глеб - беднейшее домохозяйство, имеем: а ₁= 1/3, b ₁ = 1/10.

Поскольку Глеб и Федор - два беднейших домохозяйства, имеем: а ₁ = 2/3, b ₁ = 4/10.

Точки кривой Лоренца: (0; 0), (1/3; 1/10), (2/3; 4/10), (1; 1).

Площадь фигуры, образованной отрезком ОА и кривой Лоренца, находим вычитанием из площади треугольника ОАВ площади трех фигур: треугольника (S ₁ ) и трапеций (S ₂и S ₃ ), получим

S= 0, 5 - S ₁ - S ₂ - S ₃ = 0, 167.

Коэффициент Джини равен 2 * 0, 167 = 0, 334.

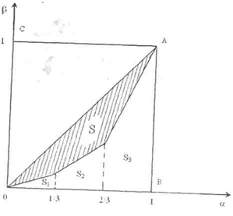
а) б)

Рис.7.1 Кривая Лоренца и коэффициент Джини:

а) общий случай; б) пример

ТИПЫ

ФИСКАЛЬНОЙ ПОЛИТИКИ

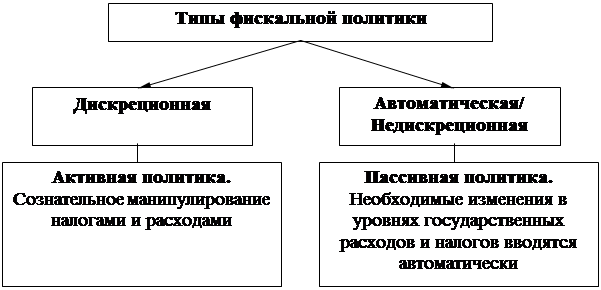
В зависимости от характера использования прямых и косвенных финансовых методов экономическая наука различает два типа фискальной политики госу­дарства:

- дискреционную;

- недискреционную.

Инструменты фискальной политики используются государством, чтобы оказать влияние на совокупный спрос и совокупное предложение, воздействуя тем самым на общую экономическую конъюнктуру, способствовать стабилизации экономической ситуации, проводить антициклические меры, противодействующие чрезмерным колебаниям экономических параметров, угрожающим возникновением кризисных явлений.