
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Знайти асимптоти кривих
|
|
1. 
| 2. 
| 3. 
|
4. 
| 5. 
| 6. 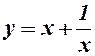
|
7. 
| 8. 
| 9. 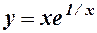
|
Відповіді: 1. 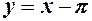 -ліва похила асимптота.
-ліва похила асимптота.
2. 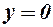 - горизонтальна асимптота.
- горизонтальна асимптота.
3.  - вертикальнаасимптота.
- вертикальнаасимптота.
4.  . 5.
. 5.  . 6.
. 6. 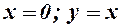
7.  . 8.
. 8.  .
.
9. 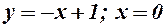 .
.
7.6. Загальна схема дослідження функцій
Нехай задана функція y=f(x). Необхідно її дослідити і на основі отриманих результатів побудувати її графік.
Схема дослідження функцій.
1. Знаходимо область визначення функції. Якщо f(x) не існує в окремих точках, напр. х=х0, то рекомендується знайти  Якщо якась із цих границь нескінченість, то х=х0 – вертикальна асимптота. Знаходимо точки перетину графіка з осями координат.
Якщо якась із цих границь нескінченість, то х=х0 – вертикальна асимптота. Знаходимо точки перетину графіка з осями координат.
2. Знаходимо похилі асимптоти.
3. Перевіряємо функцію на парність, непарність, періодичність.
Якщо f(–x)=f(x) – парна функція, то графік її симетричний відносно вісі ОY. Якщо ж функція непарна f(–x)= – f(x), то графік має центральну симетрію відносно точки О(0, 0).
4. За допомогою першої похідної f¢ (x) знаходимо інтервали, на яких f(x) зростає або спадає. Знаходимо екстремуми.
5. За допомогою другої похідної ¦¢ ¢ (х) знаходимо інтервали опуклості, угнутості, точки перегину графіка.
6. Будуємо на площині отримані характерні точки: точки перетину з осями, точки екстремумів, точки перегину. Будуємо асимптоти. І, накінець, будуємо графік функції.
Приклади дослідження функцій див. “Вказівки до розв’язування задач типового варіанту”, варіант “0”, задача 9.
Приклади для самостійного розв’язання
1.  . .
| 2. 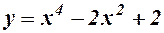 . .
| 3. 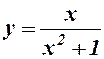 . .
|
4.  . .
| 5. 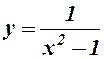 . .
| 6.  . .
|
7. 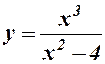 . .
| 8.  . .
| 9. 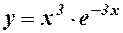 . .
|
10.  . .
| 11.  . .
| 12. 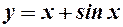 . .
|
Відповіді: 1. Область визначення  ;
;  ; для
; для 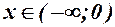 - опуклість; для
- опуклість; для  - угнутість;
- угнутість;  - точка перегину; асимптот – немає.
- точка перегину; асимптот – немає.
2. 
 - обл. визнач.;
- обл. визнач.;  ;
;  ;
; 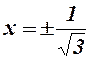 `- точки перегину; для
`- точки перегину; для 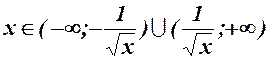 - угнутість; для
- угнутість; для 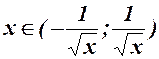 - опуклість; асимптот – немає.
- опуклість; асимптот – немає.
3. 
 - обл. визнач.;
- обл. визнач.;  ;
; 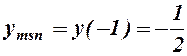 ;
; 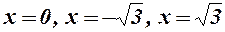 - т. перегину; для
- т. перегину; для  - опуклість; для
- опуклість; для  - угнутість;
- угнутість; 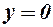 - асимптота.
- асимптота.
4. 
 - обл. визнач.;
- обл. визнач.; 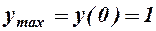 ;
; 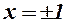 - т. перегину; для
- т. перегину; для  - угнутість; для
- угнутість; для 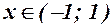 - опуклість;
- опуклість; 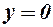 - асимптота.
- асимптота.
5. 
 - обл. визнач.;
- обл. визнач.;
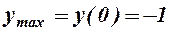 ; для
; для 
 - угнутість; для
- угнутість; для 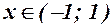 - опуклість;
- опуклість; 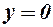 - асимптота;
- асимптота; 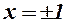 - асимптоти.
- асимптоти.
6. 
 - обл. визнач.;
- обл. визнач.; 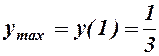 ;
;  ;
;  - т. перегину; для
- т. перегину; для  - опуклість; для
- опуклість; для  - угнутість; асимптот - немає.
- угнутість; асимптот - немає.
7. 
 - обл. визнач.;
- обл. визнач.; 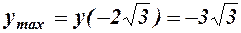 ;
;  ;
; 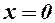 - т. перегину; для
- т. перегину; для  - опуклість; для
- опуклість; для  - угнутість;
- угнутість;  - вертик асимптота;
- вертик асимптота;  - похила асимптота.
- похила асимптота.
8. 
 - обл. визнач.;
- обл. визнач.;  ;
;  - т. перегину;
- т. перегину;  - асимптоти.
- асимптоти.
9. 
 - обл. визнач.;
- обл. визнач.;  ;
; 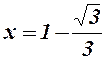
 - т. перегину;
- т. перегину; 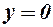 - асимптота.
- асимптота.
10. 
 - обл. визнач.;
- обл. визнач.;  ; для
; для 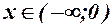 - опуклість; для
- опуклість; для  - угнутість;
- угнутість; 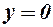 ,
, 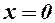 - асимптоти.
- асимптоти.
11. 
 - обл. визнач.;
- обл. визнач.;  ;
;  - т. перегину.
- т. перегину.
12. 
 - обл. визнач.; екстремумів - немає;
- обл. визнач.; екстремумів - немає;  - т. перегину.
- т. перегину.