Завдання №5. Функції

При розв’язуванні задач визначити та використовувати функції чи процедури.

1. Дано коефіцієнти многочленів P(x) i Q(x) 15-ї степені і дано дійсне число a. Обчислити величину P(a+Q(a)P(a+1)).

2. Два натуральних числа називаються «дружніми», якщо кожне з них дорівнює сумі всіх дільників іншого, за виключенням його самого (наприклад, числа 220 і 284). Надрукувати всі пари «дружніх» чисел, які не будуть більшими заданого натурального числа.

3. За заданими дійсними числами 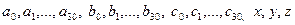обчислити величину

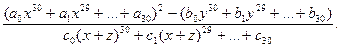
4. За заданими 50-елементними цілими масивами a, b і c обчислити

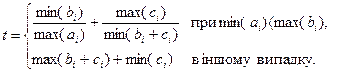
5. Задано 30-елементні дійсні вектори x, y і z. Обчислити величину (a, a)-(b, c), де a той з векторів x, y і z, який містить найбільший мінімальний елемент (вважати, що такий вектор є єдиним), b і c - два інших вектора, а (p, q) – скалярний добуток векторів p і q.

6. Дано дві квадратні дійсні матриці 10-ого порядку. Надрукувати квадрат тієї з них в якій найменший слід (сума діагональних елементів), вважаючи, що така матриця є єдина.

7. Ввести елементи дійсної матриці розміру m на n. Описати функцію сум(А), яка обчислює величину

Z=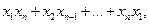

де 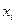- максимальний елемент і -ого ряда матриці А.

Використовуючи цю функцію, вивести значення Z.

8. Ввести два натуральні числа m та n. Обчислити 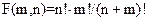Для цього визначити функцію, яка вираховує факторіал від натурального числа.

9. Описати процедуру перетворення (x, y, a, b) від чотирьох векторів, яка перетворює вектори x і y до виду:

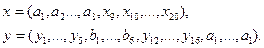
Ввести чотири дійсних вектори і вивести перетворені вектори x та y.

10.Описати логічну функцію Perestanovka (x, y), яка перевірятиме можливість отримання слова y методом переставляння літер в слові x. Ввести 5 слів і видрукувати ті з них, які переставлянням букв утворять перше введене слово.

11. Описати процедуру, яка знаходить координати максимального елемента квадратної цілочислової матриці. Ввести елементи двох квадратних матриць A і B, розміру 5х5. Використовуючи визначену процедуру поміняти місцями їх максимальні елементи. Обидві матриці видрукувати.

12. Описати процедуру sort(x), яка сортує елементи масиву x у спадному порядку методом бульбашки. Ввести два цілочислові масиви розміру n, посортувати їх і вивести.

15. Дано не порожню послідовність слів, в кожній з яких від 1 до 6 латинських літер; між сусідніми словами – кома, після останнього слова – крапка. Надрукувати ті слова, в яких однакові «сусіди», тобто співпадають попередні і наступні слова.

13. Дано 6-елементні дійсні вектори x і y і квадратні дійсні матриці A, B i C 6-ого порядку. Обчислити величину (Ax, By)+(Cx, y)/(x, By).

14. Дано три дійсні квадратні матриці 4-ого порядку. Надрукувати ту з них, норма якої є найменшою (вважати, що така матриця є одна). За норму матриці взяти максимум абсолютних величин її елементів.

15. За заданими дійсними числами c і d (с< d) обчислити

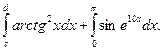
Інтеграли обчислювати наближено за формулою трапецій при n =20 для першого інтегралу і при n =100 для другого:

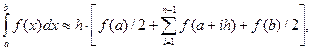
де h=(b-a)/n.

16. За заданими 40-елементними дійсними векторами x, y і z обчислити

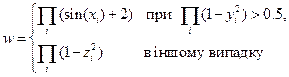
17. Ввести три дійсні вектори x, y, z. В тому з векторів x, y i z, який містить найбільше від’ємних елементів (вважати, що такий вектор один), замінити всі його додатні елементи на їхні куби – якщо це вектор x або вектор z, і на їхні обернені величини – якщо це вектор у.

18. Описати логічну функцію Poshuk(s, ss, k, n), яка перевірятиме чи входить підрядок ss в ту частину рядка s, яка починається з k -й позиції, і, якщо входить, присвоює параметру n номер позиції, з якої починається перше входження ss в цю частину рядка s. Ввести текст, використовуючи описану функцію, видрукувати всі позиції входження в нього першого слова.

19. Дано координати вершин двох трикутників. Визначити, який з них має більшу площу.

20. Дано координати вершин трикутника і координати довільної точки в ньому. Знайти відстань від даної точки до найближчої сторони трикутника. (При визначені відстані врахувати, що площа трикутника обчислюється і через три його сторони і через основу і висоту.)

21. Три прямі на площі задані рівняннями. Якщо ці прямі попарно перетинаються і складають трикутник, тоді знайти його площу.

22. Знайти найменше спільне кратне чотирьох заданих натуральних чисел.

23. Два простих числа називаються «близнюками», якщо вони відрізняються один від одного на 2 (наприклад, числа 41 і 43). Надрукувати всі пари «близнюків» з відрізка [ n, 2 n ], де n – задане ціле число більше 2.

24. Два натуральних числа називаються «дружніми», якщо кожне з них дорівнює сумі всіх дільників іншого, за виключенням його самого (наприклад, числа 220 і 284). Надрукувати всі пари «дружніх» чисел, які не будуть більшими заданого натурального числа.

25. За дійсним числом a > 0 обчислити величину

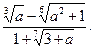
Корені 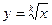обчислити з точністю 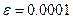за ітераційною формулою:

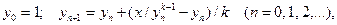
прийнявши за відповідь наближення 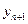, для якого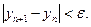

26. За дійсними числами 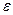> 0 і t обчислити з точністю 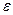величину

Для обчислення коренів використати ряд Тейлора:

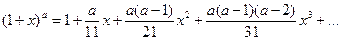
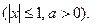
27. Дано три цілі матриці розміром 9х4. Надрукувати ту з них, де найбільше нульових рядів (якщо таких матриць декілька, надрукувати всі).

28. Дано натуральне число p і дійсні квадратні матриці А, В і С 4-ого порядку. Отримати