Combining Trigonometry Skills

Choosing The Appropriate Technique

Sometimes more than one technique from the formula table at the top of this page can be used to solve a trig problem, but you will want to choose the most efficient and easiest method to save time. The flowchart below shows how to decide which method to use:

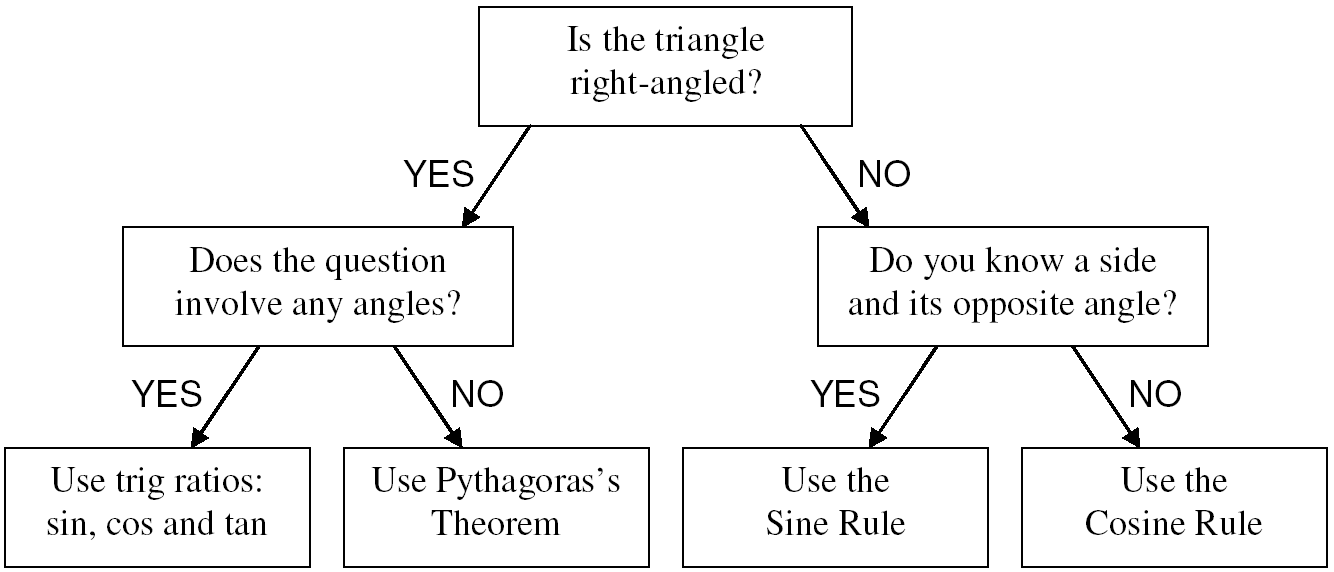
Examples

These examples illustrate the decision-making process for a variety of triangles:

e.g. 1		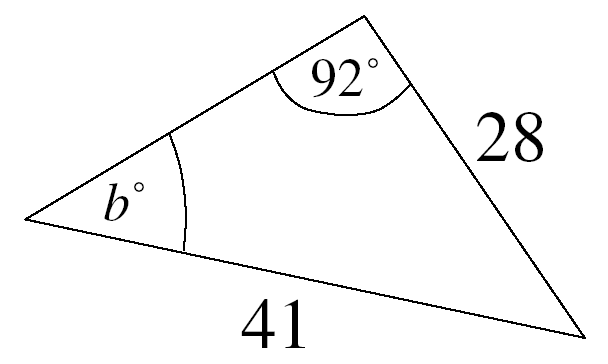1. The triangle is not right-angled. 2. We do know a side and its opposite angle. 3. Therefore we use the Sine Rule.
e.g. 2		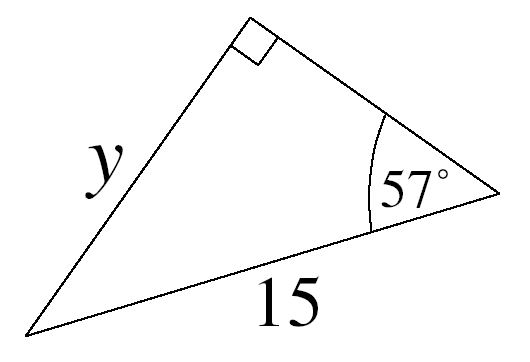1. The triangle is right-angled. 2. The question involves angles. 3. Therefore we use trig ratios - sin, cos and tan.
e.g. 3		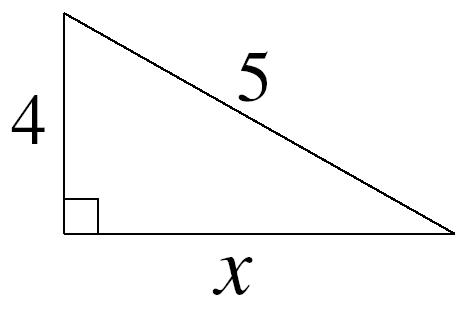1. The triangle is right-angled. 2. The question does not involve angles. 3. Therefore we use Pythagoras's Theorem.
e.g. 4		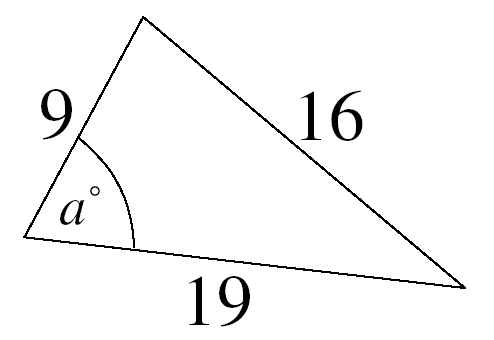1. The triangle is not right-angled. 2. We do not know a side and its opposite angle. 3. Therefore we use the Cosine Rule.

Practice Questions