
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дослідження на гетероскедастичність
|
|

Параметричний тест Гольфельда – Квандта
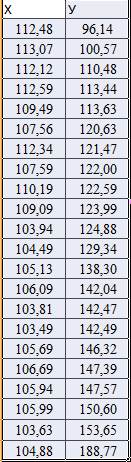 1) Сукупність значень змінної Х1 упорядковуємо за зростанням:
1) Сукупність значень змінної Х1 упорядковуємо за зростанням:
2) Визначаємо значення параметра с зі співвідношення  : n = 22, тоді с = 6. Отже, потрібно відкинути шысть елементыв із середини сукупності, але в сукупності залишається 18 елементів, таким чином n1, n2 = 8.
: n = 22, тоді с = 6. Отже, потрібно відкинути шысть елементыв із середини сукупності, але в сукупності залишається 18 елементів, таким чином n1, n2 = 8.
3) Розраховуємо лінійну модель парної регресії за першою сукупніст  :
:
 «ЛИНЕЙН 1»:
«ЛИНЕЙН 1»:
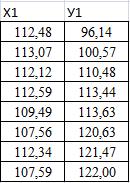
Маємо таке рівняння залежності за першою сукупністю: Ŷ 1 = 96, 14 – 112, 48 Х1 + u^,
сума квадратів залишків цієї моделі S1= 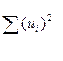 = 388, 17.
= 388, 17.
4) Розраховуємо економетричну модель парної лінійної регресії для другої сукупності 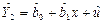 :
:
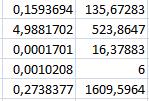 «ЛИНЕЙН 2»
«ЛИНЕЙН 2»


Маємо таке рівняння залежності для другої сукупності: Ŷ 2 = 135, 67 – 0, 1594 Х1 + u,
сума квадратів залишків для цієї моделі S2 = 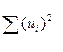 . =1609, 60
. =1609, 60
4) Знайдемо значення критерію 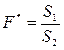 ,
, 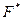 = 0, 2411
= 0, 2411
Порівняємо це значення із табличним значенням F- критерію для
k = 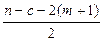 = (22– 6 – 2·2)/2 = 6.
= (22– 6 – 2·2)/2 = 6.
Значення  (0, 2411 < 5, 99). Отже, у масиві змінної Х1 гетероскедастичність відсутня.
(0, 2411 < 5, 99). Отже, у масиві змінної Х1 гетероскедастичність відсутня.