
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Частотные характеристики
|
|
Они определяются по воздействию на преобразователь синусоидального сигнала при изменение частоты в некотором рабочем диапазоне. Частотную характеристику можно получить из передаточной функции W заменив оператор P на Gомега тогда мы получаем комплексную АФХ амплетудно фазную характеристику которая будет в себе содержать в себе действительную часть D(омега) и мнимую часть G*B(ω) и тогда W(Gω)=D(ω) + G*B(ω).
Графические функция G() представляет собой годограф на местности модуль этой функции фудет АЧХ-кой K(ω)=|W(Gω)|=Корень квадратный (|D(ω)^2|+|G(ω)^2)|)
Аргументы(угол) вектора W(Gω) представляет собой АПХ.
Φ (ω)=-arctg(B(ω)/D(ω)
Arctg угол у которого тангенс.
При снятии частотной характеристики (при подачи на вход синусоидального сигнала с изменяемой частотой на выходе мы будим иметь синусоидальный сигал с той же частотой но с амплитудой и фазой зависящий от частоты сигнала т.е. X=K(ω)*sin [ω t+φ (t)]/
Необходимо отметить то что переходные и частотные характеристики аналитически получены из одного и того же исходного дифференциального уравнения то между переходными и частотными характеристиками имеется вполне определенная связь практически можно заключить что если частотная характеристика имеет пологий не спадающий характер то переходный процесс будет апериодическим если же частотная характеристика имеет подъем на одной частоте или несколько подъемов на разой частоте то это свидетельствует об резонансных свойсвтах преобразователя и о отм что переходный процесс будет колебательным.
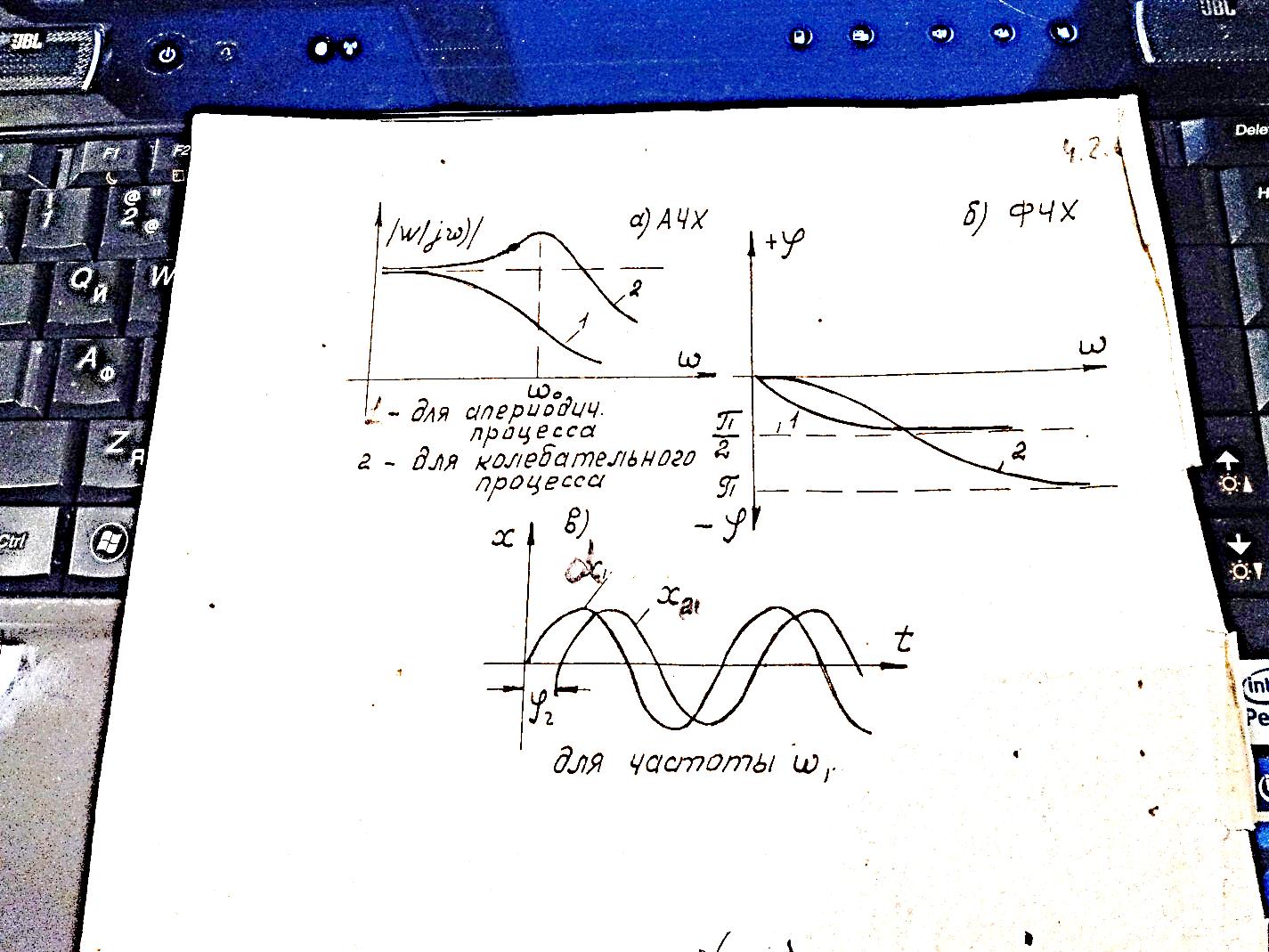
Зная выражение для переходной характеристики можно математически с помощью интегральных преобразований можно получить частотную характеристику и на оборот, зная.
Точно зная АФХ не всегда является обязательным это необходимо бывает тогда когда исследуются поля динамических процессов с помощью датчиков установленные не некотором пространстве. Например исследование вибрационного горения с камере сгорания.
Снятие АЧХ и ФЧХ представляется сложной задачей связанны с применением специальной аппаратуры так для исследования ….используются различные устройства типа сирены с диском прерывателя приводимых в движения электрическим мотором
Пр
Измерительные преобразователи могут включаться в измерительных системах в различных комбинациях. Для упрощения анализа системы могут быть обобщены свойство отдельных преобразователей и они могут быть представлены в виде типовых (простых) динамических звений.
Функция Х(У) плоскостная функция когда мы вводим эти ФЧХ и АЧХ мы переходим от этой плоскости к комплексной плоскости, которая является проекцией пространственного явления которое мы можем зарисовать.
АПХ поволяет определить вектор.
Измерительные преобразователи могут включаться в различные комбинации и образовывать сложные системы, для упрощение анализа системы могут быть обобщены отдельные свойства преобразователей и они могут быть представлены в виде отдельных звеньев.
1 Звено: пропорциональное или без инерционное.
Схема с использованием реостата.
График передаточной и переходной
АЧХ постоянна и равна этому коэффициенту
ФЧХ
Простейшим является пропорциональным без инерционным звено передаточная функция этого звена может быть представлена постоянным коэффициентом К.
Практическим этом может быть потенциометрический или реостатный преобразователь входной величиной которого является перемещение скользящего контакта и выходной напряжения U2.
К этому типу звеньев могут быть отнесены различные электронные и механические элементы
Если их инерционные свойства не значительны по сравнения с другими параметрами системы.
Апериодические или инерционные звенья наиболее широко встречаются на практике, например произведение R*C или в упрощённом виде термопара чаще применяются в измерительных системах. Колебательные звенья более сложные и в электрической интерпретации представляют собой цепочку элементов R C и L а в механическом исполнении это механизм обладающий массой упругим элементом инденфирующей (денфер – споротивляющияся среда, так среда которая система сводит к балансу) средой.
Следует отметить что передаточная функция колебательного звена имеет второй порядок, она не линейна.
При определенных параметрах три степени успокоения β =1 имеет место критический режим (граница неизвестности, может быть β больше 1 и меньше 1), для β > 1 процесс будет апериодическим это когда разность установившемся и текущем значением не изменяет знака и колебательность отсутствует, однако при таких параметров колебательного звена переходный процесс затянут и время установления будет больше, чем при колебательном движении. Тоже самое будет при β < 1 процесс будет колебательным.
Дифференцирующие звенья и интегрирующие звенья они чаще всего используются в системах автоматического регулирования и управления.
Сложные измерительные системы могут включать в себя эное количество звеньев и нам надо знать итоговое (передаточные функции) которое от группы таких звеньв.
При последовательном включения звеньев в измерительную систему результирующая передаточная функция в операторном или комплексном представлении получается как произведение передаточных функций отдельных звеньев.
W(jω)=W1(j)=W1(jω)*W2(jω)*…*Wn(jω)
если такую систему замкнуть (выходной сигнал или его часть подать на вход систему) то тем самым создадим обратную связь и изменением передаточную функцию системы. Если передаточной функции разомкнутой системы W(jω) то включение обратной связи в виде преобразователя обратной связи переменит передаточную функцию и ее результирующая передаточная функция для замкнутой системы.
Wz(jω)= W(jω)/(1+ W(jω)*Wобратная связь(jω)).
Если замкнуть обратную связь на прямую, то и сигнал подать с его выхода на вход то передаточная функция замкнутой системы будет равна.
Wz(jω)=W(jω)/(1+W(jω))
В зависимости от знака сигнала обратной связи динамические свойства системы будут изменены, могут быть применений различные виды обратной связи которые повышает стабильной устойчивой системы или на оборот повышающий ее колебательность. В каждом конкретном случае обратная связь выбирается и рассчитывается в зависимости от назначении и типа измерительной системы однако в общем можно сказать следующее: что отрицательная обратная связь когда она вычитается и уменьшает входной сигнал действует стабилизирующее и на оборот положительно обратная связь суммируясь с входным сигналом вызывает неустойчивость и колебательность.
Диапазон частот для динамических измерений достаточно широк. Начиная от 1 или долей Гц например: при исследовании устойчивость в процессе запуска двигателя распространяется до десятков кГц при исследовании вибрационных и акустических исследований.