Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Предел функции, правило Лопиталя.
|
|
Правило Лопиталя очень широко применяется для вычисления пределов, когда имеет место неопределенность вида ноль делить на ноль  , бесконечность делить на бесконечность
, бесконечность делить на бесконечность  .
.
К этим видам неопределенностей сводятся неопределенности ноль умножить на бесконечность 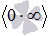 и бесконечность минус бесконечновть
и бесконечность минус бесконечновть 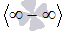 .
.
Дифференцирование функции и нахождение производной является неотъемлемой частью правила Лопиталя, так что рекомендуем обращаться к этому разделу.
Формулировка правила Лопиталя cледующая:
Если 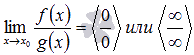 , и если функции f(x) и g(x) – дифференцируемы в окрестности точки
, и если функции f(x) и g(x) – дифференцируемы в окрестности точки 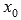 , то
, то 
В случае, когда неопределенность не исчезает после применения правила Лопиталя, то его можно применять вновь.
Рассмотрим несколько примеров и подробно разберем решения.
Пример.
Вычислить предел, используя правило Лопиталя 
Решение.
Подставляем значение
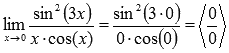
Пределы с неопределенностью данного типа можно находить по правилу Лопиталя:

Ответ:
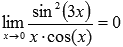
Пример.
Найти предел 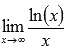
Решение.
Подставляем бесконечность
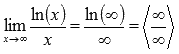
Для данного типа неопределенностей можно использовать правило Лопиталя при нахождении предела.

Ответ:
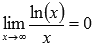
Пример.
Найти предел 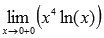
Решение.
Подставляем значение
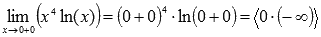
Пришли к неопределенности вида ноль умножить на бесконечность. Обращаемся ктаблице неопределенностей для выбора метода решения. Преобразуем выражение, чтобы можно было применить правило Лопиталя.
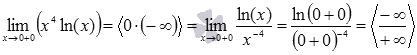
Пришли к неопределенности бесконечность делить на бесконечность, а значит, можно найти предел по правилу Лопиталя.
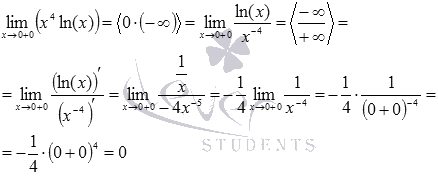
Ответ:
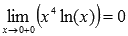
Пример.
Найти предел 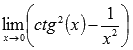
Решение.
Подставляем значение
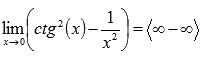
Пришли к неопределенности бесконечность минус бесконечность. Преобразуем выражение, чтобы можно было применить правило Лопиталя.

Последний переход был сделан при использовании первого замечательного предела. Теперь можно найти предел по правилу Лопиталя.
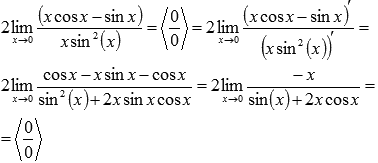
Неопределенность не исчезла, поэтому применим правило Лопиталя еще раз.

Ответ: