
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Гиперболические функции
|
|
Функции 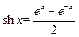 и
и 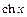 =
= 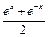 , определённые на
, определённые на  , называются гиперболическим синусом и гиперболическим косинусом.
, называются гиперболическим синусом и гиперболическим косинусом.
Функция 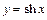 – нечётная, строго возрастающая, функция
– нечётная, строго возрастающая, функция  – чётная, строго убывающая на
– чётная, строго убывающая на 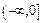 и строго возрастающая на
и строго возрастающая на  , в точке
, в точке 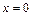 имеет минимум –
имеет минимум – 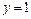 . Графики этих функций представлены на рисунках 1-2. Пунктирные кривые на рис. 1 отвечают функциям
. Графики этих функций представлены на рисунках 1-2. Пунктирные кривые на рис. 1 отвечают функциям 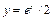 и
и 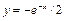 , а на рис. 2 - функциям
, а на рис. 2 - функциям 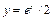 и
и 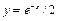 .
.
Гиперболические тангенс и котангенс определяются формулами:
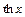 =
= 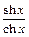 ,
,  ,
, 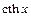 =
=  ,
,  ,
, 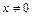 .
.
Обе функции нечётные, 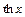 монотонно возрастает, а
монотонно возрастает, а 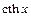 монотонно убывает, их графики изображены на рисунках 3, 4 (пунктиром обозначены асимптоты функций):
монотонно убывает, их графики изображены на рисунках 3, 4 (пунктиром обозначены асимптоты функций):
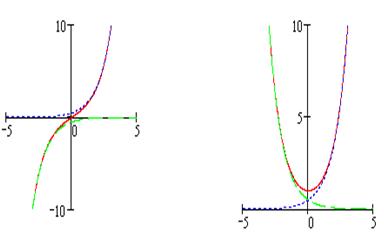
Рис. 1 Рис. 2

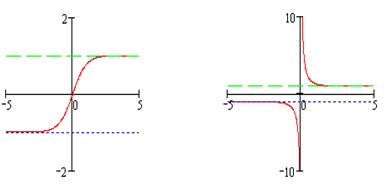
Рис. 3 Рис. 4
Название этих функций – синус, косинус, тангенс, котангенс – связано с тем, что эти функции имеют ряд свойств, аналогичных свойствам тригонометрических функций. Так, имеют место формулы (обратить внимание на знаки!):
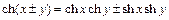 ,
,  ,
,
из них, в частности, при 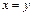 , следует:
, следует:


 .
.
Докажем, например, первую из этих формул:
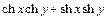 =
= 
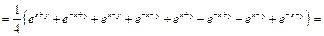
 . Так же проверяются и остальные.
. Так же проверяются и остальные.
Запишем ещё ряд формул для гиперболических функций:

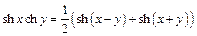 ,
, 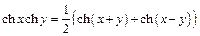 ,
,  , откуда
, откуда 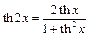 ,
, 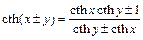 , откуда
, откуда 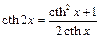 ,
, 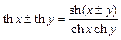 ,
, 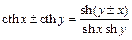 .
.
Функции 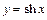 и
и 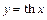 ,
,  , обратимы, их обратные функции обозначаются соответственно
, обратимы, их обратные функции обозначаются соответственно  (ареасинус гиперболический) и
(ареасинус гиперболический) и 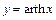 (ареатангенс гиперболический). Действительно, решая уравнение
(ареатангенс гиперболический). Действительно, решая уравнение
 или
или 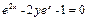 относительно
относительно 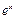 , найдём
, найдём  , откуда, выбирая знак «+» перед радикалом, ведь
, откуда, выбирая знак «+» перед радикалом, ведь 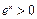 , получим
, получим  .
.
Аналогично из уравнения 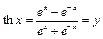 или
или 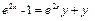 найдём
найдём  , откуда
, откуда  ,
,  .
.
Графики функций  и
и 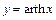 (а, значит, и найденных функций
(а, значит, и найденных функций 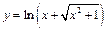 и
и  ) изображены на рисунках 5 и 6 (пунктирные линии на рис. 6 отвечают асимптотам функции
) изображены на рисунках 5 и 6 (пунктирные линии на рис. 6 отвечают асимптотам функции 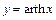 ).
).
Рассмотрим функции  и
и 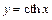 . Решая уравнение
. Решая уравнение
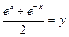 или
или  относительно
относительно 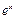 , найдём при
, найдём при

Рис. 5
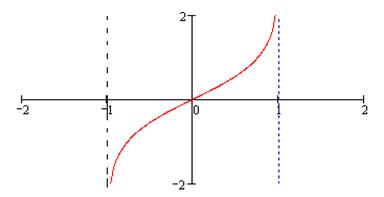
Рис. 6
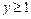 два значения
два значения 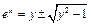 , откуда
, откуда  - получим двузначную функцию, которая распадается на две однозначных ветви:
- получим двузначную функцию, которая распадается на две однозначных ветви:  - обратная для
- обратная для  на
на  и
и 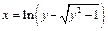 - обратная для
- обратная для  на
на 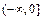 . На рис. 7 изображён график функций
. На рис. 7 изображён график функций  (сплошная линия) и
(сплошная линия) и
 (пунктирная кривая):
(пунктирная кривая):
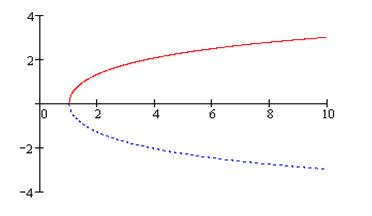
Рис. 7
Из уравнения  или
или 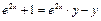 найдём:
найдём: 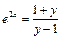 , откуда
, откуда 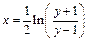 ,
, 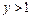 .
.
График функции 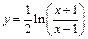 приведён на рис. 8 (пунктиром обозначены асимптоты данной функции).
приведён на рис. 8 (пунктиром обозначены асимптоты данной функции).
Эпитет «гиперболический» в названии рассмотренных функций связан с тем, что формулы  параметрически задают гиперболу:
параметрически задают гиперболу:  - каноническое уравнение гиперболы.
- каноническое уравнение гиперболы.
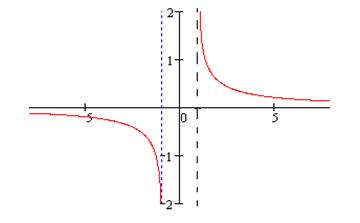
Рис. 8
|