Деление отрезка в данном отношении.

НЕДЕЛЯ 2

Лекция 3.

Координаты точки на прямой и плоскости.

Деление отрезка в данном отношении.

В основе метода координат лежит понятие системы координат.

Две взаимно перпендикулярные оси О_х и О_у, имеющие общее начало О и одинаковую масштабную единицу, образуют прямоугольную систему координат. Ось О_х называется осью абсцисс, ось О_у – осью ординат.

В прямоугольной системе координат О_ху точку М, имеющую координаты х и у, обозначают М(х; у), где х – абсцисса точки, а у – её ордината.

Пусть в прямоугольной системе координат заданы точки М₁(х_1, у₁) и М₂(х₂; у₂). Расстояние между ними определяется по формуле:

(1)

Три точки плоскости, не лежащие на одной прямой образуют треугольник.

Теорема. Для любых трех точек А(х₁; у₁), В(х₂; у₂) и С(х₃; у₃), не лежащих на одной прямой, площадь S треугольника АВС вычисляется по формуле

(2)

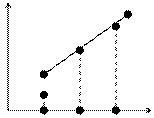
Пусть на плоскости дан произвольный отрезок М₁М₂ и пусть М – любая точка этого отрезка, отличная от точки М₂ (рис.1).

Координаты точки М(х; у) делящей отрезок между точками М₁(х₁; у₁) и М₂(х₂; у₂) в заданном отношении λ, определяются по формулам:

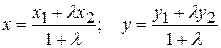(3)

При λ =1 получаем формулы для координат середины отрезка:

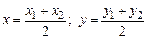(4)

у М₂(х₂; у₂)

М₁(х₁; у₁) М(х; у) ρ М

φ

О Р₁ Р Р₂ х O

рис.1 рис.2

В полярной системе координат положение точки М на плоскости определяется её расстоянием |ОМ|=ρ от полюса О (ρ –полярный радиус-вектор точки) и углом φ, образованным отрезком ОМ с полярной осью ОЕ (рис.2). Угол φ считается положительным при отсчете от полярной оси против часовой стрелки.

Прямоугольные координаты х и у точки М и её полярные координаты ρ и φ связаны следующими формулами

Литература: К, А, Хасеинов Каноны математики. Стр.61-63.