Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Эллипс.
|
|
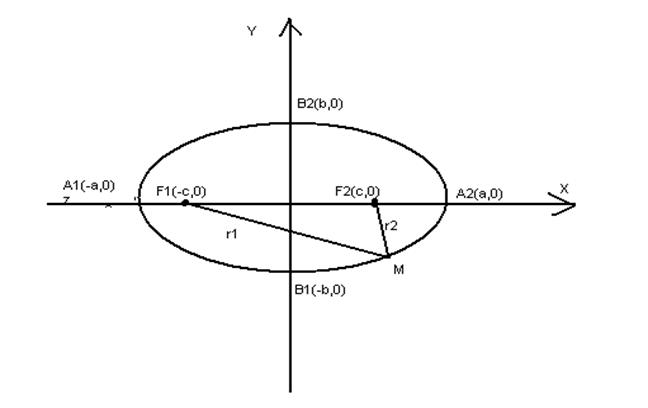
Определение 2. Эллипсом называется геометрическое место точек плоскости, сумма расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная (обозначают 2а), большая, чем расстояние между фокусами (2а> 2с).
Каноническое уравнение эллипса имеет вид
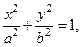
где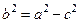 
. Число c – половина расстояния между фокусами, числа a и b называют большой и малой полуосями эллипса.
В случае a= b эллипс представляет собой окружность радиуса a с центром в начале координат. Форма эллипса характеризуется эксцентриситетом
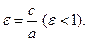
Расстояние от некоторой точки М эллипса до его фокусов называются фокальными радиусами этой точки. Они вычисляются по следующим формулам
,
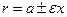здесь знак «+» берется для левого фокального радиус-вектора, а знак «-» – для правого фокального радиус вектора.
Гипербола.
Определение 3. Гиперболой называется геометрическое место точек плоскости, разность расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная (обозначают 2а), меньшая, чем расстояние между фокусами (2а< 2с).
Каноническое уравнение гиперболы имеет вид
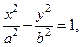
где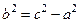 
. Число c – половина расстояния между фокусами, числа a и b называют действительной и мнимой полуосями гиперболы. Форма гиперболы характеризуется эксцентриситетом
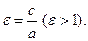
Расстояние от некоторой точки М эллипса до его фокусов называются фокальными радиусами этой точки. Они вычисляются по следующим формулам
,
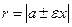здесь знак «+» берется для левого фокального радиус-вектора, а знак «-» – для правого фокального радиус вектора.
Если a=b, то уравнение
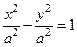или 
определяет равнобочную гиперболу.
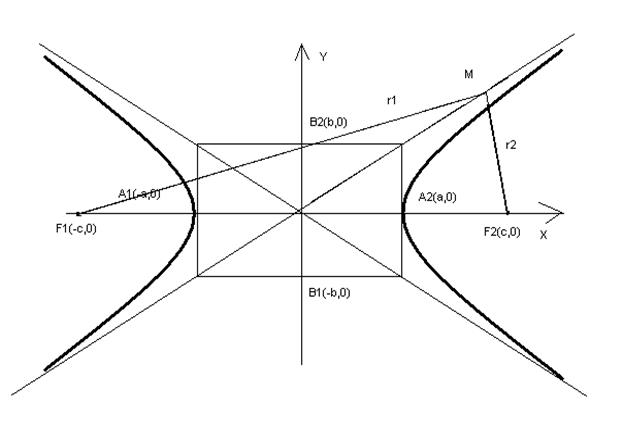
Две гиперболы, определяемые уравнениями
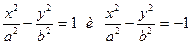
называются сопряженными.