
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методичні вказівки до розв’язання задачі
|
|
Обчислимо середні значення та стандартні відхилення пояснюючих змінних 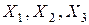 . Для цього можна скористатись стандартними функціями MS Excel. В майстрі функцій знайдемо категорію “статистичні”і в ній функції “СРЗНАЧ” та “СТАНДОТКЛ”.
. Для цього можна скористатись стандартними функціями MS Excel. В майстрі функцій знайдемо категорію “статистичні”і в ній функції “СРЗНАЧ” та “СТАНДОТКЛ”.
Дані величини можна також розрахувати за формулами:
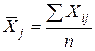 , (1)
, (1)
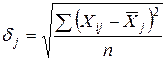 , (2)
, (2)
де 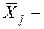 середнє значення
середнє значення 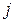 -тої пояснюючої змінної;
-тої пояснюючої змінної;
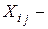 індивідуальне значення
індивідуальне значення 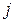 -тої пояснюючої змінної;
-тої пояснюючої змінної;
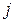 – номер пояснюючої змінної;
– номер пояснюючої змінної;
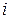 – номер точки спостереження (місяця);
– номер точки спостереження (місяця);
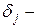 стандартне відхилення
стандартне відхилення 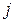 -тої пояснюючої змінної;
-тої пояснюючої змінної;
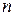 – число спостережень.
– число спостережень.
Додаткові розрахунки наведено в табл.1.
Таблиця 1 – Проміжні розрахунки
| Місяць | 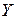
| 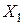
| 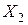
| 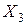
| 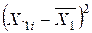
| 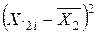
| 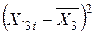
|
| 36, 6025 | 21, 16 | 23, 04 | |||||
| 1, 1025 | 6, 76 | 3, 24 | |||||
| 25, 5025 | 12, 96 | 14, 44 | |||||
| 16, 4025 | 6, 76 | 7.84 | |||||
| 4, 2025 | 12, 96 | 0, 04 | |||||
| 9, 3025 | 21, 16 | 23, 04 | |||||
| 16, 4025 | 12, 96 | 14, 44 | |||||
| 1, 1025 | 0, 36 | 3, 24 | |||||
| 36, 6025 | 21, 16 | 0, 64 | |||||
| 0, 0025 | 0, 16 | 0, 04 | |||||
| 3, 8025 | 1, 96 | 4, 84 | |||||
| 1, 1025 | 0, 16 | 1, 44 | |||||
| 0, 0025 | 5, 76 | 1.44 | |||||
| 0, 9025 | 2, 56 | 0.04 | |||||
| 3, 8025 | 0, 36 | 4, 84 | |||||
| 15, 6025 | 19, 36 | 10, 24 | |||||
| 35, 4025 | 29, 16 | 17, 64 | |||||
| 8, 7025 | 11, 56 | 0, 04 | |||||
| 48, 3025 | 40, 96 | 17, 64 | |||||
| 80, 1025 | 70, 56 | 27, 04 | |||||
| Всього | 344, 95 | 298, 80 | 175.21 |
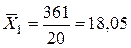 ;
; 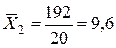 ;
; 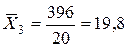 .
.
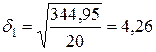 ;
; 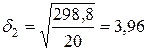 ;
; 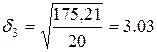 .
.
2. Нормалізуємо пояснюючі змінні. Серед статистичних функцій MS Excel знайдемо функцію “НОРМАЛІЗАЦІЯ” та нормалізуємо 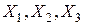 .
.
Для цього можна також скористатись формулою:

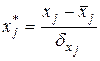 (3)
(3)
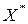 = =
| 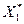
| 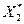
| 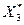
|
| -1, 41989 | -1, 15996 | -1, 58071 | |
| -0, 24643 | -0, 65563 | -0, 59276 | |
| -1, 1852 | -0, 9078 | -1, 25139 | |
| -0, 9505 | -0, 65563 | 0, 92208 | |
| -0, 48112 | -0, 9078 | 0, 065963 | |
| -0, 71581 | -1, 15996 | -1, 58071 | |
| -0, 9505 | -0, 9078 | -1, 25139 | |
| -0, 24643 | -0, 1513 | -0, 59276 | |
| -1, 41989 | -1, 15996 | -0, 26345 | |
| -0, 01173 | 0, 100866 | 0, 065863 | |
| 0, 45765 | 0, 353032 | 0, 72449 | |
| -0, 24643 | 0, 100866 | 0, 395176 | |
| -0, 01173 | 0, 605198 | 0, 395176 | |
| 0, 222958 | -0, 40347 | 0, 065863 | |
| 0, 45765 | -0, 1513 | 0, 72449 | |
| 0, 927034 | 1, 10953 | 1, 053804 | |
| 1, 396419 | 1, 361696 | 1, 383117 | |
| 0, 692342 | 0, 857364 | 0, 065863 | |
| 1, 631111 | 1, 613862 | 1, 383117 | |
| 2, 100496 | 2, 118194 | 1, 712431 |
Транспонуємо матрицю 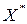 (нормалізовану) в матрицю
(нормалізовану) в матрицю 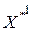
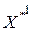 = =
| -1, 4199 | -0, 2464 | -1, 1852 | -0, 9505 | -0, 4811 | -0, 7158 | -0, 9505 |
| -1, 16 | -0, 6556 | -0, 9078 | -0, 6556 | -0, 9078 | -1, 16 | -0, 9078 | |
| -1, 5807 | -0, 5928 | -1, 2514 | -0, 9221 | 0, 06596 | -1, 5807 | -1, 2514 |
Продовження матриці 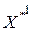
| -0, 2464 | -1, 4199 | -0, 0117 | 0, 45765 | -0, 2464 | -0, 0117 | 0, 22296 | 0, 45765 |
| -0, 1513 | -1, 16 | -0, 10087 | 0, 35303 | 0, 10087 | 0, 6052 | -0, 4035 | -0, 1513 |
| -0, 5928 | -0, 2635 | 0, 06586 | 0, 72449 | 0, 39518 | 0, 39518 | 0, 06586 | 0, 72449 |
Закінчення матриці 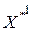
| 0, 92703 | 1, 39642 | 0, 69234 | 1, 63111 | 2, 1005 |
| 1, 10953 | 1, 3617 | 0, 85736 | 1, 61386 | 2, 11819 |
| 1, 0538 | 1, 38312 | 0, 06586 | 1, 38312 | 1, 71243 |
Перемножимо матриці 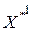 та
та 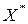 :
:
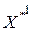 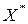 = =
| 17, 8964552 | 16, 9413894 | |
| 17, 8964552 | 16, 6415575 | ||
| 16, 9413894 | 16, 6415575 |
3. Знайдемо кореляційну матрицю 
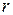 .
.
Для знаходження кореляційної матриці 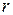 необхідно кожний елемент матриці
необхідно кожний елемент матриці 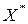
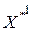 помножити на
помножити на 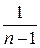 (у нашому випадку
(у нашому випадку 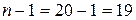 ):
):
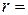
| 0, 941918693 | 0, 891652074 | |
| 0, 941918693 | 0, 875871449 | ||
| 0, 891652074 | 0, 875871449 |
4. Знайдемо визначник матриці 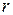
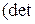
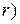 .
.
Для знаходження 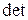
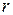 необхідно серед математичних функцій MS Excel знайти функцію “МОПРЕД”. Скориставшись нею, дістанемо:
необхідно серед математичних функцій MS Excel знайти функцію “МОПРЕД”. Скориставшись нею, дістанемо: 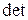
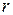 = 0, 02182033.
= 0, 02182033.
Оскільки 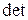
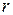 наближається до нуля, то в масиві пояснюючих змінних може існувати мультиколінеарність.
наближається до нуля, то в масиві пояснюючих змінних може існувати мультиколінеарність.
Прологарифмуємо визначник матриці 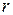 :
: 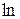
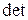
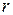 = -3, 824913185
= -3, 824913185
5. Обчислимо критерій Пірсона 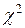 за формулою:
за формулою:
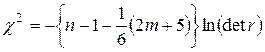 , (4)
, (4)
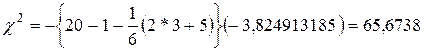 .
.
Знайдене значення 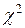 порівняємо з табличним значенням
порівняємо з табличним значенням 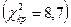 , коли маємо
, коли маємо 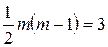 ступенів свободи та при рівні значущості
ступенів свободи та при рівні значущості 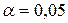 .
.
Оскільки  , то в масиві пояснюючих змінних (продуктивність праці, питомі інвестиції та фондовіддача) існує мультиколінеарність.
, то в масиві пояснюючих змінних (продуктивність праці, питомі інвестиції та фондовіддача) існує мультиколінеарність.
6. Обчислимо 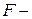 критерій.
критерій.
Для визначення 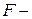 критеріїв необхідно знайти матрицю
критеріїв необхідно знайти матрицю 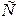 , яка є оберненою до матриці
, яка є оберненою до матриці 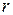 :
:

| 10, 67120467 | -7, 375970017 | -3, 05460023 |
| -7, 375970017 | 9, 392918454 | -1, 65019013 | |
| -3, 054600232 | -1, 65019013 | 5, 168995053 |
Безпосередньо 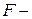 критерій обчислюється за формулою:
критерій обчислюється за формулою:
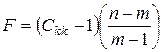 , (5)
, (5)
де 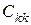 – діагональний елемент матриці
– діагональний елемент матриці 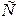 .
.
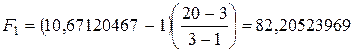 ;
;
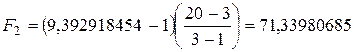 ;
;
 .
.
Обчислені критерії порівнюються з табличним значенням 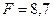 , коли є
, коли є 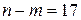 ступенів свободи та при рівні значущості
ступенів свободи та при рівні значущості 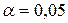 .
.
У розглядуваному випадку 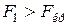 ,
, 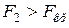 ,
, 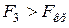 . Це означає, що кожна з пояснюючих змінних мультиколінеарна з іншими.
. Це означає, що кожна з пояснюючих змінних мультиколінеарна з іншими.
7. Визначимо частинні коефіцієнти кореляції 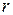 .
.
Частинні коефіцієнти кореляції показують тісноту зв’язку між двома пояснюючими змінними за умови, що всі інші змінні не впливають на цей зв’язок і обчислюються за формулою:
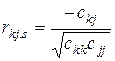 . (6)
. (6)
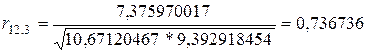 ;
;
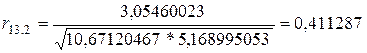 ;
;
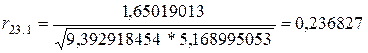 .
.
Отже, спираючись на здобуті нами значення окремих (частинних) коефіцієнтів кореляції, можна сказати, що зв’язок між фондовіддачею та продуктивністю праці є тісним, якщо не враховувати вплив питомих інвестицій, зв’язок між фондовіддачею та питомими інвестиціями є слабким, якщо не брати до уваги вплив продуктивності праці. Зв’язок між продуктивністю праці та питомими інвестиціями також є слабким, якщо не враховувати фондовіддачу.
8. Визначимо 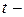 критерій.
критерій.
Ці критерії застосовуються для визначення мультиколінеарності двох пояснюючих змінних і обчислюються за формулою:
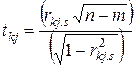 . (7)
. (7)
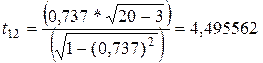 ;
;
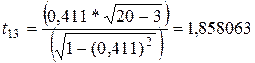 ;
;
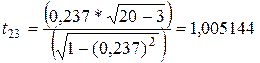 .
.
Обчислені 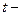 критерії порівнюються з табличним значенням
критерії порівнюються з табличним значенням 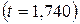 , коли маємо
, коли маємо 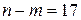 ступенів свободи та при рівні значущості
ступенів свободи та при рівні значущості 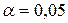 .
.
Оскільки 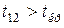 , то продуктивність праці та фондовіддача є відповідно мультиколінеарними між собою;
, то продуктивність праці та фондовіддача є відповідно мультиколінеарними між собою;
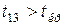 , тому відповідно продуктивність праці та питомі інвестиції є мультиколінеарними між собою;
, тому відповідно продуктивність праці та питомі інвестиції є мультиколінеарними між собою;
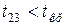 , тому продуктивність праці та питомі інвестиції не є мультиколінеарними між собою.
, тому продуктивність праці та питомі інвестиції не є мультиколінеарними між собою.
Висновок. Дослідження, проведені за алгоритмом Фаррара-Глобера показали, що мультиколінеарність між пояснюючими змінними даного прикладу існує. Отже, для того, щоб можна було застосувати метод 1МНК для оцінювання параметрів моделі за цією інформацію, необхідно в першу чергу звільнитися від мультиколінеарності.