Теорема Пифагора.

Введение.

Что такое метрическое соотношение в треугольнике я узнал только в 8 классе. Сначала я подумал, что это не самая интересная тема в математике, но когда я начал читать литературу по этой теме, провел большое количество времени в интернете я понял, что это очень интересная и даже легкая тема.

Метрическими соотношениями называют формулы, связывающие длины различных отрезков, величины различных углов в треугольнике, его площадь и т.п. Важнейшими из этих соотношений являются теоремы косинусов и синусов; другие примеры – формула для длины медианы, формула Герона, формула Эйлера для расстояния между центрами вписанной и описанной окружностей. И в своей работе я хочу показать вам некоторые примеры метрический соотношений в треугольнике.

Теорема Пифагора.

Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.

Алгебраическая формулировка: В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b:

a ² + b ² = c ²

Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся напрямую из аксиом.

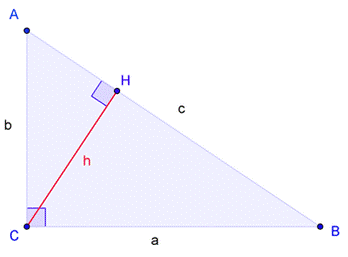
Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения

| BC | = a, | AC | = b, | AB | = c

получаем

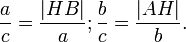
Что эквивалентно

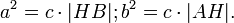
Сложив, получаем

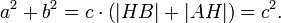
или

a ² + b ² = c ², что и требовалось доказать