
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
II. Неопределенность вида .
|
|
Тема III. Дифференциальное исчисление функции
С одной переменной.
Правило Лопиталя».
Изучив уже производную и дифференциал функции с одной переменной, мы снова возвращаемся к вычислению пределов функций, так как в случаях вычисления пределов, приводящих к «неопределенностям» вида
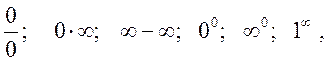
иногда применяют правило Лопиталя, которое использует понятие производной и дает возможность раскрыть указанные неопределенности.
Теорема Лопиталя. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле.
Рассмотрим случаи, когда теорема Лопиталя применяется непосредственно и когда ее применение становится возможным после некоторых несложных преобразований.
I. Неопределенности вида 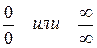 (непосредственное применение теоремы Лопиталя).
(непосредственное применение теоремы Лопиталя).
Если  , причем функции
, причем функции 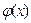 и
и 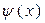 определены в интервале, содержащем точку a, и имеют в этом интервале конечные производные
определены в интервале, содержащем точку a, и имеют в этом интервале конечные производные
(причем 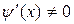 ) и если
) и если 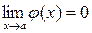 и
и 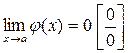 или
или 
 и
и 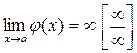 , то
, то 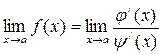 , при условии, что этот предел существует или равен
, при условии, что этот предел существует или равен  .
.
В случае, если 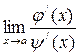 снова представляет собою неопределенность вида
снова представляет собою неопределенность вида 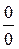 или
или 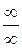 , применяют правило Лопиталя повторно и т.д.
, применяют правило Лопиталя повторно и т.д.
Пример: 
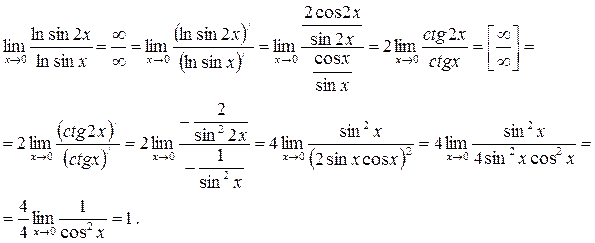
САМОСТОЯТЕЛЬНО: Вычислить пределы функций:
1. 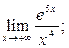 2.
2.  ; 3.
; 3. 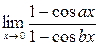 .
.
II. Неопределенность вида.
Если 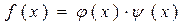 и
и 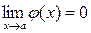 ,
, 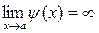 , то для нахождения предела
, то для нахождения предела  функцию преобразуют к виду
функцию преобразуют к виду 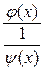 или
или 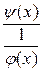 ,
,
что приводит к случаю 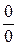 или
или 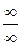 , т.е. непосредственному применению правила Лопиталя.
, т.е. непосредственному применению правила Лопиталя.
Пример:

САМОСТОЯТЕЛЬНО: Вычислить пределы функций:
1.  2.
2.  ; 3.
; 3. 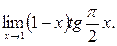
III. Неопределенность вида 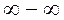 .
.
Если 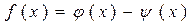 и
и  ,
, 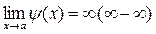 , то для нахождения предела
, то для нахождения предела 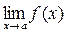 разность
разность  алгебраически преобразуют к виду
алгебраически преобразуют к виду 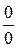 или
или 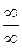 . Это можно сделать различными способами, например:
. Это можно сделать различными способами, например: 
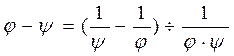 .
.
Пример:
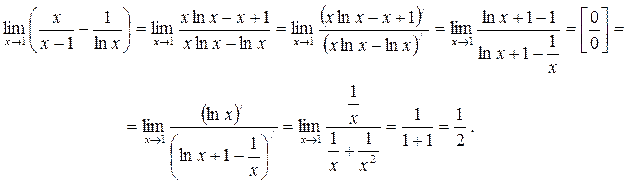

САМОСТОЯТЕЛЬНО: Вычислить пределы функций:
1. 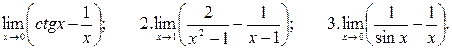
|