
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оформление контрольной работы
|
|
Контрольная работа должна включать следующие элементы:
· титульный лист;
· содержание;
· практическая часть работы;
· список литературы.
При выполнении контрольной работы задачи следует выполнять в том порядке, в каком они даны в задании. Условие задачи приводится полностью, а ее решение отделяется интервалом. Решение задач должны содержать развернутые расчеты, пояснения и краткие выводы. По возможности решение задач необходимо оформлять в виде таблиц. Расчет относительных показателей нужно производить с точностью до 0, 001, а процентов – до 0, 1. Исчисленные показатели должны содержать единицы измерения, допускаются только общепринятые сокращения.
Контрольная работа должна быть оформлена аккуратно, написана разборчиво и без зачеркиваний. Таблицы и графики следует оформлять в соответствии с требованиями, принятыми в статистике. В конце работы необходимо привести список использованной литературы (автор, название, издательство и год издания).
Работа должна быть подписана студентом с указанием даты ее выполнения.
Кафедра допускает к защите только те работы, которые удовлетворяют всем предъявляемым требованиям и правильно оформлены.
Титульный лист представляет собой единый, установленного образца бланк, который студент оформляет в соответствии с индивидуальными данными. Образец оформления титульного листа курсовой работы приведен в приложении 1.
Варианты контрольных работ
| А, Б | 1, 11, 21, 31, 41, 51, 61 | 2, 12, 22, 32, 42, 52, 62 | 3, 13, 23, 33, 43, 53, 63 | 4, 14, 24, 34, 44, 54, 64 | 5, 15, 25, 35, 45, 55, 65 | 6, 16, 26, 36, 46, 56, 66 | 7, 17, 27, 37, 47, 57, 67 | 8, 18, 28, 38, 48, 58, 68 | 9, 19, 29, 39, 49, 59, 69 | 10, 20, 30, 40, 50, 60, 69 |
| В, Г | 10, 19, 26, 44, 50, 57, 63 | 1, 20, 25, 41, 36, 51, 64 | 2, 11, 24, 37, 42, 52, 65 | 3, 12, 23, 38, 43, 53, 66 | 4, 13, 22, 39, 44, 54, 67 | 5, 14, 21, 40, 45, 55, 68 | 6, 15, 29, 31, 46, 56, 69 | 7, 16, 21, 32, 47, 57, 61 | 8, 17, 22, 33, 48, 58, | 9, 18, 22, 34, 49, 59, 63 |
| Д, Е | 9, 17, 23, 32, 49, 55, 63 | 10, 18, 24, 33, 50, 56, 64 | 1, 19, 25, 34, 41, 57, 65 | 2, 20, 29, 35, 42, 58, 66 | 3, 11, 26, 36, 43, 59, 67 | 4, 12, 27, 37, 44, 60, 68 | 5, 13, 28, 38, 45, 51, 69 | 6, 13, 29, 39, 46, 52, 61 | 7, 15, 30, 40, 47, 53, 62 | 8, 16, 21, 31, 48, 54, 63 |
| Ж, З | 8, 15, 26, 33, 48, 55, 69 | 9, 16, 27, 34, 49, 56, 61 | 10, 17, 28, 35, 50, 57, 62 | 1, 18, 29, 36, 41, 58, 63 | 2, 19, 30, 37, 42, 59, 64 | 3, 20, 21, 38, 43, 60, 65 | 4, 11, 22, 39, 44, 51, 66 | 5, 12, 23, 40, 45, 52, 67 | 6, 13, 24, 31, 46, 53, 68 | 7, 14, 25, 32, 47, 54, 69 |
| И, Й, К | 7, 13, 24, 32, 47, 55, 67 | 8, 14, 25, 33, 48, 56, 68 | 9, 15, 26, 34, 49, 57, 69 | 10, 1627, 3550, 58, 61 | 1, 17, 28, 36, 41, 59, 62 | 2, 18, 29, 37, 42, 60, 63 | 3, 19, 30, 38, 43, 51, 64 | 4, 20, 21, 39, 44, 53, 65 | 5, 11, 22, 40, 45, 54, 66 | 6, 12, 23, 32 46, 55, 67 |
| Л, М | 6, 12, 24, 3546, 56, 62 | 7, 13, 24, 3647, 57, 61 | 8, 14, 26, 37 48, 58, 66 | 9, 15, 27, 3849, 59, 65 | 10, 16, 28, 39 50, 60, 64 | 1, 17, 29, 4041, 51, 63 | 2, 12, 28, 30, 31, 52, 62 | 3, 14, 21, 3343, 53, 61 | 4, 20, 22, 36, 44, 54, 69 | 5, 11, 23, 3745, 55, 68 |
| Н, О | 5, 12, 25, 3845, 56, 65 | 6, 13, 26, 3946, 57, 66 | 7, 14, 27, 4047, 58, 67 | 8, 15, 28, 31 48, 59, | 9, 16, 29, 32, 49, 60, 69 | 10, 17, 30, 33, 50, 51, 61 | 1, 18, 21, 3441, 52, | 2, 19, 22, 35, 42, 53, | 3, 20, 23, 36, 43, 54, | 4, 11, 24, 37, 44, 55, 65 |
| П, Р | 4, 11, 27, 3144, 53, | 5, 12, 28, 35, 45, 54, | 6, 13, 29, 34, 46, 55, | 7, 14, 30, 31, 47, 56, | 8, 15, 21, 33, 48, 57, | 9, 16, 22, 32, 49, 58, | 10, 17, 23, 31, 50, 59, | 1, 18, 24, 40, 41, 60, | 2, 19, 25, 39, 42, 51, | 3, 20, 26, 38, 43, 52, |
| С, Т | 3, 15, 27, 33, 43, 51, | 4, 16, 28, 34, 44, 52, | 5, 17, 29, 35, 45, 60, 65 | 6, 18, 30, 36, 46, 59, | 7, 19, 21, 37, 47, 58, | 8, 20, 22, 38, 48, 57, | 9, 11, 23, 39, 49, 56, | 10, 12, 24, 40, 50, 55, | 1, 13, 25, 31, 41, 54, | 2, 14, 26, 32, 42, 53, |
| У, Ф | 2, 15, 22, 31, 42, 52, 68 | 3, 16, 23, 38, 43, 53, | 4, 17, 24, 39, 44, 54, | 5, 18, 25, 40 45, 55, 62 | 6, 19, 26, 31, 46, 56, 63 | 7, 20, 27, 32, 47, 57, 64 | 8, 11, 28, 33, 48, 58, 65 | 9, 12, 29, 34 49, 59, 66 | 10, 13, 30, 35, 50, 60, 67 | 1, 14, 21, 36 41, 51, 68 |
| Х, Ц | 9, 15, 24, 34, 49, 52, 69 | 10, 16, 25, 3850, 53, 68 | 1, 17, 26, 39 41, 54, 67 | 2, 18, 27, 4042, 55, 66 | 3, 19, 28, 31 43, 56, 65 | 4, 20, 29, 3244, 57, 64 | 5, 13, 30, 33 45, 58, 63 | 6, 15, 24, 34, 46, 59, 62 | 7, 19, 21, 35 47, 60, 61 | 8, 20, 23, 3648, 54, 69 |
| Ч, Ш | 8, 11, 29, 37 48, 55, 67 | 9, 14, 25, 38 49, 56, 68 | 10, 19, 26, 3950, 57, 69 | 1, 20, 27, 32, 41, 58, 61 | 2, 15, 28, 35 42, 59, 62 | 3, 16, 22, 32, 43, 60, 63 | 4, 11, 30, 37 44, 51, 64 | 5, 12, 21, 35 45, 52, 65 | 6, 17, 22, 39, 46, 53, 66 | 7, 18, 23, 36, 47, 54, 67 |
| Щ, Э | 7, 12, 24, 37, 47, 55, | 8, 15, 25, 40, 48, 56, | 9, 18, 26, 33, 49, 58, | 10, 11, 27, 38 50, 59, | 1, 14, 23, 38, 41, 60, | 2, 17, 24, 39, 42, 51, 61 | 3, 20, 25, 31, 43, 53, 62 | 4, 13, 26, 32 44, 54, 63 | 5, 16, 27, 33 45, 55, 64 | 6, 19, 28, 34 46, 56, 65 |
| Ю, Я | 6, 13, 22, 37 46, 54, 68 | 7, 16, 23, 38, 47, 52, 69 | 8, 17, 24, 37, 48, 53, 61 | 9, 12, 25, 36, 49, 52, 62 | 10, 13, 26, 35 50, 51, 63 | 1, 18, 27, 34, 41, 5460, | 2, 19, 28, 33 42, 55, 69 | 3, 14, 29, 32, 43, 59, 68 | 4, 15, 30, 39, 44, 58, 67 | 5, 20, 26, 37, 45, 57, 66 |
Тема 1: Сводка и группировка статистических данных.
При решении данных задач необходимо выполнить аналитическую группировку. При этом важно понять суть аналитической группировки, с помощью которой исследуются взаимосвязи изучаемых признаков.
Задача 1.
Имеются данные 25 предприятий одной из отраслей экономики:
| № п/п | Среднегодовая стоимость основных производственных фондов, тыс. руб. | Стоимость произведенной продукции, тыс. руб. |
С целью изучения зависимости между среднегодовой стоимостью основных производственных фондов и объемом произведенной продукции произведите группировку по среднегодовой стоимости основных производственных фондов, образовав три группы предприятий с равными интервалами.
По каждой группе и совокупности предприятий в целом подсчитайте:
1) число предприятий;
2) среднегодовую стоимость основных производственных фондов - всего и в среднем на одно предприятие;
3) стоимость продукции - всего и в среднем на одно предприятие;
4) размер продукции на один рубль основных производственных фондов (фондоотдачу).
Результаты расчетов представьте в виде групповой таблицы. Сделайте выводы.
Задача 2
За изучаемый период имеются следующие данные о работе малых предприятий отрасли:
| № п/п | Произведено продукции, тыс. т | Сумма затрат на производство продукции, тыс. руб. |
| 3, 6 | ||
| 4, 6 | ||
| 5, 5 | ||
| 4, 8 | ||
| 2, 7 | ||
| 2, 9 | ||
| 7, 5 | ||
| 6, 3 | ||
| 4, 1 | ||
| 4, 8 | ||
| 7, 6 | ||
| 6, 5 | ||
| 11, 5 | ||
| 10, 6 | ||
| 9, 0 | ||
| 6, 9 | ||
| 5, 0 | ||
| 11, 2 | ||
| 8, 1 | ||
| 7, 8 | ||
| 4, 2 | ||
| 6, 3 | ||
| 12, 1 | ||
| 9, 8 | ||
| 8, 5 |
Для изучения зависимости между объемом произведенной продукции и затратами на ее производство произведите группировку предприятий по объему произведенной продукции, образовав три группы с равными интервалами.
По каждой группе и по совокупности предприятий в целом подсчитайте:
1) число предприятий;
2) объем произведенной продукции всего и в среднем на одно предприятие;
3) сумму затрат на производство продукции всего и на одно предприятие.
Результаты представьте в виде групповой таблицы и сделайте выводы.
Задача 3.
Имеются следующие данные по 25 предприятиям одной из отраслей промышленности:
| № п/п | Возраст оборудования, лет | Затраты на капитальный ремонт, млн. руб. | |
| 5, 6 | 6, 7 | ||
| 6, 8 | 23, 0 | ||
| 10, 6 | 24, 2 | ||
| 3, 9 | 12, 0 | ||
| 7, 0 | 20, 0 | ||
| 8, 4 | 14, 8 | ||
| 8, 0 | 27, 0 | ||
| 5, 8 | 6, 9 | ||
| 6, 4 | 10, 0 | ||
| 8, 5 | 15, 0 | ||
| 3, 9 | 9, 3 | ||
| 5, 2 | 13, 0 | ||
| 7, 5 | 16, 7 | ||
| 4, 0 | 8, 0 | ||
| 3, 5 | 9, 5 | ||
| 10, 2 | 24, 5 | ||
| 6, 2 | 14, 1 | ||
| 4, 3 | 10, 9 | ||
| 3, 5 | 9, 0 | ||
| 6, 0 | 11, 0 | ||
| 6, 2 | 10, 2 | ||
| 3, 0 | 8, 0 | ||
| 8, 9 | 12, 6 | ||
| 9, 0 | 14, 0 | ||
| 4, 0 | 15, 0 | ||
Для изучения зависимости между возрастом оборудования и затратами на капитальный ремонт произведите группировку предприятий по возрасту оборудования, образовав три группы с равными интервалами.
По каждой группе и по совокупности заводов в целом подсчитайте:
1) число заводов;
2) возраст оборудования всего и в среднем на одно предприятие;
3) суммут затрат на капитальный ремонт всего и в среднем на одно предприятие.
Результаты расчетов представьте в таблице. Сделайте выводы.
Задача 4.
За отчетный период имеются следующие данные о реализации товаров и издержках обращения по предприятиям торговли района, млн. руб.
| № п/п | Розничный товарооборот | Сумма издержек обращения |
| 5, 1 | 0, 30 | |
| 5, 6 | 0, 34 | |
| 7, 0 | 0, 46 | |
| 4, 6 | 0, 30 | |
| 3, 3 | 0, 15 | |
| 3, 9 | 0, 25 | |
| 6, 4 | 0, 42 | |
| 4, 4 | 0, 26 | |
| 5, 0 | 0, 16 | |
| 4, 2 | 0, 34 | |
| 5, 0 | 0, 37 | |
| 4, 2 | 0, 28 | |
| 2, 0 | 0, 18 | |
| 6, 6 | 0, 39 | |
| 6, 5 | 0, 36 | |
| 6, 2 | 0, 36 | |
| 3, 8 | 0, 25 | |
| 5, 5 | 0, 38 | |
| 7, 5 | 0, 44 | |
| 6, 6 | 0, 37 | |
| 4, 5 | 0, 27 | |
| 5, 6 | 0, 35 | |
| 6, 0 | 0, 40 | |
| 4, 0 | 0, 24 | |
| 3, 5 | 0, 24 |
Для выявления зависимости между объемом розничного товарооборота и издержками обращения сгруппируйте предприятия по объему розничного товарооборота, образовав три группы с равными интервалами.
По каждой группе и совокупности предприятий в целом подсчитайте:
1) число предприятий;
2) объем товарооборота всего и в среднем на одно предприятие;
3) сумму издержек обращения всего и в среднем на одно предприятие;
4) относительный уровень издержек обращения (процентное отношение суммы издержек обращения к объему розничного товарооборота).
Результаты расчетов представьте в виде группой таблицы. Напишите краткие выводы.
Задача 5.
Имеются данные 25 предприятий одной из отраслей промышленности:
| № п/п | Среднегодовая стоимость основных производственных фондов, тыс. руб. | Прибыль, тыс. руб. |
| 42, 0 | ||
| 104, 5 | ||
| 58, 0 | ||
| 53, 7 | ||
| 80.5 | ||
| 94, 3 | ||
| 11, 2 | ||
| 34, 7 | ||
| 70, 8 | ||
| 29, 2 | ||
| 33, 1 | ||
| 54, 0 | ||
| 50, 3 | ||
| 70, 5 | ||
| 79, 0 | ||
| 64, 3 | ||
| 46, 1 | ||
| 41, 5 | ||
| 38, 3 | ||
| 85, 1 | ||
| 18.9 | ||
| 46, 4 | ||
| 52, 0 | ||
| 90, 3 | ||
| 86, 7 |
С целью изучения зависимости между среднегодовой стоимостью основных производственных фондов и размером прибыли произведите группировку заводов по среднегодовой стоимости основных производственных фондов, образовав три группы с равными интервалами. По каждой группе и совокупности заводов в целом подсчитайте:
1) число заводов;
2) среднегодовую стоимость основных производственных фондов всего и в среднем на один завод;
3) прибыль всего и в среднемна один завод;
4) размер прибыли на 1 руб. основных производственных фондов.
Результаты расчетов представьте в виде групповой таблицы. Напишите краткие выводы.
Задача 6.
Имеются следующие выборочные данные по 22-м предприятиям одной из отраслей промышленности (выборка 10%-ная, механическая):
| № п/п | Численность промышленно-производственного персонала, чел. | Выпуск продукции, млн. руб. |
| 99, 0 | ||
| 27, 0 | ||
| 53, 0 | ||
| 57, 0 | ||
| 115, 0 | ||
| 62, 0 | ||
| 86, 0 | ||
| 19, 0 | ||
| 130, 0 | ||
| 83, 0 | ||
| 55, 0 | ||
| 147, 0 | ||
| 101, 0 | ||
| 64, 0 | ||
| 44, 0 | ||
| 144, 0 | ||
| 178, 0 | ||
| 135, 0 | ||
| 100, 0 | ||
| 135, 0 | ||
| 99, 0 | ||
| 141, 0 |
С целью изучения зависимости между численностью промышленно-производственного персонала и выпуском продукции произведите группировку предприятий по численности промышленно-производственного персонала, образовав три группы с равными интервалами. По каждой группе и совокупности предприятий в целом подсчитайте:
1) число предприятий;
2) среднюю численность промышленно-производственного персонала всего и в среднем на одно предприятие;
3) выпуск продукции всего и в среднемна одно предприятие;
4) объем выпуска продукции на одного работника.
Результаты расчетов представьте в виде групповой таблицы. Напишите краткие выводы.
Задача 7.
За изучаемый период имеются следующие данные о работе малых предприятий отрасли:
| № п/п | Выпуск продукции, тыс. руб. | Прибыль, тыс. руб. |
| 15, 7 | ||
| 12, 1 | ||
| 15, 5 | ||
| 12, 9 | ||
| 17, 1 | ||
| 9, 2 | ||
| 15, 9 | ||
| 17, 6 | ||
| 18, 5 | ||
| 20, 1 | ||
| 6, 4 | ||
| 14, 6 | ||
| 16, 7 | ||
| 17, 4 | ||
| 14, 6 | ||
| 14, 8 | ||
| 16, 1 | ||
| 18, 7 | ||
| 16, 4 | ||
| 16, 8 | ||
| 16, 5 | ||
| 18, 5 | ||
| 19, 1 |
Для изучения зависимости между объемом произведенной продукции и прибылью предприятия произведите группировку предприятий по объему произведенной продукции, образовав три группы с равными интервалами.
По каждой группе и по совокупности предприятий в целом подсчитайте:
1) число предприятий;
2) объем выпуска продукции всего и в среднем на одно предприятие;
3) величину прибыли всего и на одно предприятие.
Результаты представьте в виде групповой таблицы и сделайте выводы.
Задача 8.
Имеются данные по 20 банкам одного из регионов.
| Названия банков | Уставной капитал, млн. руб. | Работающие активы, млн. руб. |
| 4, 8 | 17, 1 | |
| 5, 6 | 6, 9 | |
| 4, 6 | 4, 9 | |
| 3, 6 | 3, 9 | |
| 11, 7 | 17, 9 | |
| 10, 2 | 15, 7 | |
| 10, 9 | 15, 5 | |
| 12, 4 | 19, 5 | |
| 7, 4 | 10, 9 | |
| 3, 3 | 2, 3 | |
| 2, 7 | 2, 0 | |
| 4, 6 | 6, 9 | |
| 2, 9 | 3, 2 | |
| 4, 5 | 5, 2 | |
| 3, 3 | 4, 0 | |
| 2, 9 | 4, 4 | |
| 2, 7 | 3, 2 | |
| 9, 4 | 9, 9 | |
| 8, 9 | 11, 7 | |
| 10, 3 | 12, 4 |
С целью изучения зависимости между размером активов и уставным капиталом произведите группировку банков по размеру уставного капитала, образовав четыре группы с равными интервалами.
По каждой группе и совокупности банков подсчитайте:
1) число банков;
2) размер уставного капитала всего и в среднем на один банк;
3) размер активов всего и в среднем на один банк.
Результаты расчетов представьте в виде групповой таблицы, сделайте краткие выводы.
Задача 9.
За изучаемый период имеются следующие данные о стоимости квартир в городе:
| № п/п | Площадь, м2 | Цена квартиры, млн. руб. |
| 1, 58 | ||
| 2, 2 | ||
| 1, 9 | ||
| 2, 2 | ||
| 1, 6 | ||
| 2, 1 | ||
| 1, 82 | ||
| 60, 2 | 2, 15 | |
| 2, 2 | ||
| 1, 95 | ||
| 2, 0 | ||
| 2, 0 | ||
| 3, 1 | ||
| 1, 9 | ||
| 60, 2 | 2, 2 | |
| 4, 1 | ||
| 2, 9 | ||
| 36, 6 | 1, 75 | |
| 4, 2 | ||
| 2, 7 | ||
| 3, 3 | ||
| 2, 9 | ||
| 1, 9 | ||
| 3, 3 | ||
| 2, 26 |
Для изучения зависимости между площадью квартиры и её стоимостью произведите группировку по размеру площади, образовав пять групп с равными интервалами.
По каждой группе и по совокупности квартир в целом подсчитайте:
1) число квартир;
2) общий размер площади и средний размер одной квартиры;
3) общую стоимость квартир группы и одной квартиры.
Результаты представьте в виде групповой таблицы и сделайте выводы.
Задача 10.
Имеются данные о стоимости земельных участков под индивидуальную застройку в г.Оренбурге
| № п/п | Площадь, 100 м2 | Цена участка, млн. руб. |
| 0, 25 | ||
| 0, 72 | ||
| 1, 88 | ||
| 2, 6 | ||
| 0, 64 | ||
| 0, 87 | ||
| 1, 68 | ||
| 0, 9 | ||
| 2, 5 | ||
| 4, 7 | ||
| 2, 82 | ||
| 5, 0 | ||
| 4, 4 | ||
| 1, 5 | ||
| 1, 32 | ||
| 2, 5 | ||
| 2, 9 | ||
| 4, 3 | ||
| 4, 0 | ||
| 3, 8 | ||
| 4, 95 | ||
| 4, 75 | ||
| 0, 5 | ||
| 1, 5 | ||
| 3, 3 |
Для изучения зависимости между размером участка и его стоимостью произведите группировку по размеру площади участков, образовав пять групп с равными интервалами.
По каждой группе и по совокупности участков в целом подсчитайте:
1) число участков;
2) общую площадь участков и средний размер одного участка;
3) общую цену участков и цену одного участка.
Результаты представьте в виде групповой таблицы и сделайте выводы.
Методические указания по решению задач:
При решении данных задач предусматривается выполнение аналитической группировки. При этом важно понять суть аналитической группировки, с помощью которой исследуются взаимосвязи изучаемых признаков.
Группировкой называется расчленение единиц статистической совокупности на группы, однородные по какому-либо одному или нескольким признакам.
Аналитическая группировка позволяет установить наличие и направление взаимосвязи между факторными и результативными признаками в пределах однородной совокупности. Группировка единиц совокупности производится по факторному признаку. Для составления аналитической группировки требуется определить величину интервала по формуле:
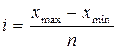 , (1)
, (1)
где xmax максимальное значение факторного признака в совокупности,
xmin – минимальное значение факторного признака в совокупности,
n – число групп.
Число групп может быть задано (на основе опыта предыдущих обследований). В том случае, если вопрос о числе групп приходится решать самостоятельно, можно использовать формулу Стерджесса для определения оптимального числа групп:
k=1 + 3, 322 lg N, (2)
где N — число единиц в совокупности.
Полученное значение следует округлить для облегчения расчетов. Процедуру округления при расчете интервала проводят всегда. Трехзначное, четырехзначное или большее число округляют до ближайшего числа, кратного 50 или 100. Если число имеет два знака до запятой и несколько знаков после запятой, его округляют до целого, если один знак до запятой и несколько знаков после запятой — до десятых и т.д.
Затем определяется число единиц в каждой из образованных групп, а также объем варьирующих признаков в пределах созданных групп и исчисляются средние размеры результативно показателя (признака) по каждой группе. Результаты группировки оформляются в виде групповой аналитической таблицы.
Анализ рядов распределения провести на основе их графического изображения. Для этого нужно построить графики – полигон и гистограмму. Полигон используется при изображении дискретных вариационных рядов. Дискретный вариационный ряд характеризует распределение единиц совокупности по дискретному признаку, принимающему только целые значения. Гистограмма применяется для изображения интервального вариационного ряда. Построение интервальных вариационных рядов целесообразно, прежде всего, при непрерывной вариации признака, а также, если дискретная вариация проявляется в широких пределах, т.е. число вариантов прерывного признака достаточно велико. В заключение необходимо дать экономический анализ показателей групповой таблицы и сделать выводы.
Тема: Средние величины и показатели вариации в статистике
В данных задачах представлены интервальные вариационные ряды распределения, которые необходимо преобразовать в дискретные исчислить среднее значение признака, дисперсию, среднее квадратическое отклонение и коэффициент вариации.
Задача 11.
С целью изучения уровня оплаты труда рабочих предприятия проведена 10%-ная механическая выборка, в результате которой получено следующее распределение рабочих по средней заработной плате:
| Средняя заработная плата, руб. | Численность рабочих, чел. | ||
| менее 5000 | |||
| 5200-5600 | |||
| 5600-6000 | |||
| свыше 6000 | |||
| Итого | |||
На основе этих данных вычислите:
1) среднюю заработную платуодного рабочего;
2) моду и медиану
3) среднее квадратическое отклонение;
4) коэффициент вариации;
5) с вероятностью 0, 954 возможные границы, в которых ожидается средняя заработная плата на предприятии;
Задача 12.
С целью изучения уровня оплаты труда рабочих предприятия проведена 10%-ная механическая выборка, в результате которой получено следующее распределение рабочих по средней заработной плате:
| Средняя заработная плата, руб. | Численность рабочих, чел. | ||
| менее 6000 | |||
| 6000-12000 | |||
| 1200-20000 | |||
| свыше 20000 | |||
| Итого | |||
На основе этих данных вычислите:
1) среднюю заработную платуодного рабочего;
2) моду и медиану
3) среднее квадратическое отклонение;
4) коэффициент вариации;
5) с вероятностью 0, 954 возможные границы, в которых ожидается средняя заработная плата на предприятии;
Задача 13.
В целях изучения норм расходования сырья при изготовлении продукции на заводе проведена 5%-ная собственно-случайная выборка, в результате которой получено следующее распределение изделий по массе:
| Масса изделия, г | Число изделий, шт. |
| до 20 20-22 22-24 24-26 свыше 26 | |
| Итого |
На основе этих данных вычислите:
1) среднюю массу изделия;
2) моду и медиану
3) среднее квадратическое отклонение;
4) коэффициент вариации;
5) с вероятностью 0, 997 возможные границы, в которых ожидается средняя масса изделия всей партии изготовленных изделий;
Сделайте выводы.
Задача 14.
Для характеристики размера балансовой прибыли строительных фирм проведена 10 % -ная собственно-случайная выборка, в результате которой получено следующее распределение фирм по размеру прибыли:
| Балансовая прибыль, млн. руб. | Число банков |
| 10-20 20-30 30-40 40-50 свыше 50 | |
| Итого |
На основе приведенных данных определите:
1) среднюю прибыль по совокупности фирм;
2) моду и медиану;
3) среднее квадратическое отклонение;
4) коэффициент вариации;
5) с вероятностью 0, 954 возможные границы, в которых ожидается средняя прибыль в банках в данном регионе;
Задача 15.
С целью изучения норм расходования сырья на изготовление единицы продукции проведена 10%-ная механическая выборка, в результате которой получено следующее распределение:
| Расход сырья, г | Количество изделий, шт. |
| до 20 | |
| 20 – 24 | |
| 24 – 28 | |
| 28 – 32 | |
| свыше 32 | |
| Итого |
На основе представленных данных вычислите:
1) средний расход сырья на одно изделие;
2) моду и медиану;
3) среднее квадратическое отклонение;
4) коэффициент вариации;
5) с вероятностью 0, 954 возможные границы, в которых ожидаетсясредний расход сырья для всей партии изделий;
Задача 16.
В целях изучения затрат времени на изготовление единицы продукции на предприятии проведена 5 % - ная механическая выборка, в результате которой получено следующее распределение по затратам времени:
| Затраты времени на единицу продукции, мин. | Количество единиц, шт. |
| До 20 20-24 24-28 28 - 32 32 и более | |
| Итого |
На основе этих данных вычислите:
1) средние затраты времени на изготовление единицы продукции;
2) моду и медиану;
3) среднее квадратическое отклонение;
4) коэффициент вариации;
5) с вероятностью 0, 954 возможные границы, в которых ожидаются средние затраты времени на изготовление единицы продукции
Задача 17.
В целях изучения стажа рабочих завода проведена 36-% механическая выборка, в результате которой получено следующее распределение рабочих по стаж работы
| Стаж, число лет | Число рабочих, чел. |
| менее 5 | |
| 5-10 | |
| 10-15 | |
| 15-20 | |
| 20-25 | |
| свыше 25 | |
| Итого |
На основе этих данных вычислите:
1) средний стаж рабочих завода;
2) моду и медиану
3) среднее квадратическое отклонение;
4) коэффициент вариации;
5) с вероятностью 0, 997 возможные границы, в которых ожидается средний стаж рабочих всего завода.
Задача 18.
В целях изучения затрат времени на изготовление единицы продукции на предприятии проведена 5 %-ная механическая выборка, в результате которой получено следующее распределение по затратам времени:
| Затраты времени на единицу продукции, мин. | Количество единиц, шт. |
| До 40 40-50 50-70 70 - 80 80 и более | |
| Итого |
На основе этих данных вычислите:
1) средние затраты времени на изготовление единицы продукции;
2) моду и медиану;
3) среднее квадратическое отклонение;
4) коэффициент вариации;
5) с вероятностью 0, 954 возможные границы, в которых ожидаются средние затраты времени на изготовление единицы продукции.
Задача 19.
По данным выборочного наблюдения распределение оценочных компаний по количеству заказов за период, характеризуется следующими данными:
| Группы оценочных компаний по числу заказов | Число компаний |
| До 50 | |
| 50 – 70 | |
| 70 – 90 | |
| 90 – 110 | |
| 110 – 130 | |
| Свыше 130 |
Определите:
1) среднее число заказов на одну организацию;
2) моду и медиану;
3) среднее квадратическое отклонение;
4) коэффициент вариации.
Постройте гистограмму и полигон распределения оценочных компаний по числу заказов. По результатам расчетов сделайте выводы.
Задача 20.
В целях изучения затрат времени на проведение оценщиком замера земельного участка в оценочной фирме проведена 5 %-ная механическая выборка, в результате которой получено следующее распределение по затратам времени:
| Затраты времени на выполнение замеров, мин. | Количество замеров, шт. |
| До 15 15-20 20-35 35 - 45 45 и более | |
| Итого |
На основе этих данных вычислите:
1) средние затраты времени на осуществление замеров;
2) моду и медиану;
3) среднее квадратическое отклонение;
4) коэффициент вариации;
Постройте гистограмму и полигон распределения замеров по их продолжительности. По результатам расчетов сделайте выводы.
Методические указания по решению задач:
Средняя величина — это обобщающая характеристика множества индивидуальных значений некоторого количественного признака.
Средняя, являясь функцией множества индивидуальных значений, представляет одним значением всю совокупность и отражает то общее, что присуще всем ее единицам.
В статистике используются различные виды (формы) средних величин. Наиболее часто применяются следующие средние величины:
• средняя арифметическая;
• средняя гармоническая;
• средняя геометрическая;
• средняя квадратическая.
Указанные средние величины относятся к классу степенных средних. Они могут быть вычислены, либо когда каждый вариант (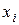 ) в данной совокупности встречается только один раз, при этом средняя называется простой или невзвешенной, либо когда варианты повторяются различное число раз, при этом число повторений вариантов называется частотой (
) в данной совокупности встречается только один раз, при этом средняя называется простой или невзвешенной, либо когда варианты повторяются различное число раз, при этом число повторений вариантов называется частотой ( ) или статистическим весом, а средняя, вычисленная с учетом весов, — средней взвешенной..
) или статистическим весом, а средняя, вычисленная с учетом весов, — средней взвешенной..
Введем условное обозначение 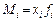 и рассмотрим формулы расчета степенных средних (таблица).
и рассмотрим формулы расчета степенных средних (таблица).
Таблица – Виды средних и формулы их расчета
| Вид средней | Формула расчета | Вид средней | Формула расчета |
| Арифметическая простая | 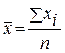
| Геометрическая простая | 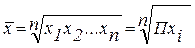
|
| Арифметическая взвешенная | 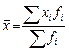
| Геометрическая взвешенная | 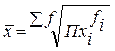
|
| Гармоническая Простая | 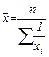
| Квадратическая простая | 
|
| Гармоническая взвешенная | 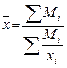
| Квадратическая взвешенная | 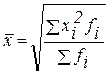
|
Выбор вида средней базируется на исходном соотношении средней (логической формуле). Это соотношение представляет собой отношение 2-х экономических категорий, которые приводят к исходному искомый средний показатель. Для каждого среднего показателя можно составить только одно исходное соотношение, независимо от формы представления исходных данных:
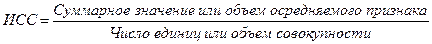
1 Если имеется ряд данных по двум взаимосвязанным показателям, для одного из которых нужно вычислить осредняемую величину, и при этом известны численные значения знаменателя логической формулы, а числитель неизвестен, но может быть найден как произведение этих показателей, среднюю вычисляют по формуле арифметической взвешенной.
2 Если известны численные значения числителя логической формулы, а значения знаменателя неизвестны, но могут быть найдены как частное от деления одного показателя на другой, то средняя рассчитывается по формуле гармонической взвешенной.
3 Если имеются численные значения числителя и знаменателя логической формулы, то средняя вычисляется непосредственно по этой формуле.
В статистике кроме степенных средних находят применение и структурные средние – мода, медиана, квартили, децили, перцентили..
Мода - это величина признака (варианта), наиболее часто повторяющаяся в изучаемой совокупности. Для дискретных рядов распределения модой будет значение варианты с наибольшей частотой.
Для интервальных рядов распределения с равными интервалами мода определяется по формуле:
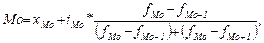
где 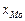 - начальное значение интервала, содержащего моду;
- начальное значение интервала, содержащего моду;
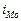 - величина модального интервала;
- величина модального интервала;
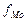 - частота модального интервала;
- частота модального интервала;
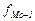 - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному;
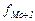 - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.
Медиана - это варианта, расположенная в середине вариационного ряда. Если ряд распределения дискретный и имеет нечетное число членов, то медианой будет варианта, находящаяся в середине упорядоченного ряда (упорядоченный ряд - это расположение единиц совокупности в возрастающем или убывающем порядке).
Если упорядоченный ряд состоит из четного числа членов, то медианой будет средняя арифметическая из двух вариант, расположенных в середине ряда. Для определения медианы надо подсчитать сумму накопленных частот ряда. Наращивание итога продолжается до получения накопленной суммы частот, превышающей половину. Если же сумма накопленных частот против одной из вариант равна точно половине сумме частот, то медиана определяется как средняя арифметическая этой варианты и последующей.
Медиана интервального вариационного ряда распределения определяется по формуле
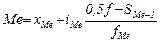
где 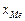 — начальное значение интервала, содержащего медиану;
— начальное значение интервала, содержащего медиану;
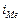 — величина медианного интервала;
— величина медианного интервала;
 — сумма частот ряда;
— сумма частот ряда;
 — сумма накопленных частот, предшествующих медианному интервалу;
— сумма накопленных частот, предшествующих медианному интервалу;
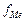 — частота медианного интервала.
— частота медианного интервала.
Расчет дисперсии производится по формуле:

Среднее квадратическое отклонение представляет собой корень второй степени из среднего квадрата отклонений отдельных значений признака от их средней, т. е. оно исчисляется путем извлечения квадратного корня и измеряется в тех же единицах, что и варьирующий признак. Среднее квадратическое отклонение показывает: на сколько в среднем отклоняются конкретные варианты от его среднего значения. Формула расчета следующая:
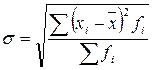 .
.
Коэффициент вариации рассчитывается по формуле:
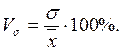
Выражаются в процентах и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%. Далее ряды распределения изобразить графически и сделать по произведенным расчетам выводы.
Тема: Ряды динамики и их анализ
Задачи составлены на расчет и анализ аналитических показателей динамических рядов, которые определяются по формулам (для удобства и наглядности исходные и рассчитанные показатели изложите в табличной форме, предварительно дав название ей.
Задача 21.
Производство цемента предприятиями Оренбургской области характеризуется следующими данными:
| Годы | Выпуск, млн. шт. |
| 46, 3 | |
| 37, 8 | |
| 35, 9 | |
| 31, 0 | |
| 34, 0 | |
| 41, 9 | |
| 38, 8 |
Для анализа динамики производства цемента за 2005-2011 гг. вычислите:
1. цепные и базисные абсолютные приросты, темпы роста и темпы прироста, абсолютное содержание одного процента прироста; полученные показатели представьте в таблице и постройте график;
2. средние показатели динамики производства цемента;
Сделайте выводы.
Задача 22.
Валовой сбор зерна сельскохозяйственного предприятия характеризуется следующими данными:
| Годы | Валовой сбор зерна, тыс. т |
| 21, 7 18, 1 10, 9 19, 1 18, 3 16, 4 25, 0 |
Для анализа динамики производства зерна за 2005-2011 гг. вычислите:
1 цепные и базисные абсолютные приросты, темпы роста и темпы прироста, абсолютное содержание одного процента прироста; полученные показатели представьте в таблице и постройте график;
2 средние показатели динамики производства зерна;
Сделайте выводы.
Задача 23
Урожайность зерновых культур в сельскохозяйственном предприятии характеризуется следующимиданными:
| Годы | Урожайность, ц/га |
| 10, 7 | |
| 12, 8 | |
| 6, 4 | |
| 9, 8 | |
| 11, 3 | |
| 9, 9 | |
| 13, 2 |
Для анализа динамики урожайности зерновых культур за 2005-2011 гг. вычислите:
1. цепные и базисные абсолютные приросты, темпы роста и темпы прироста, абсолютное содержание одного процента прироста; полученные показатели представьте в таблице и постройте график;
2. средние показатели динамики урожайности зерновых культур;
Сделайте выводы.
Задача 24.
Динамика численности крупных и средних предприятий промышленности в Оренбуржье характеризуется следующимиданными:
| Годы | Число предприятий |
Для анализа динамики численности крупных и средних предприятий промышленности за 2005-2011 гг. вычислите:
1. цепные и базисные абсолютные приросты, темпы роста и темпы прироста, абсолютное содержание одного процента прироста; полученные показатели представьте в таблице и постройте график;
2. средние показатели динамики численности предприятий;
Сделайте выводы.
Задача 25.
Динамика электровооруженности труда на одном из предприятий промышленности области характеризуется следующимиданными:
| Годы | Электровооруженность, кВт∙ ч/чел.-ч |
| 3, 33 | |
| 3, 59 | |
| 3, 84 | |
| 4, 07 | |
| 3, 88 | |
| 4, 10 | |
| 4, 05 |
Для анализа динамики электровооруженности промышленного предприятия за 2005-2011 гг. вычислите:
1) цепные и базисные абсолютные приросты, темпы роста и темпы прироста, абсолютное содержание одного процента прироста; полученные показатели представьте в таблице и постройте график;
2) средние показатели динамики электровооруженности предприятий;
Сделайте выводы.
Задача 26.
Просроченная задолженность по оплате труда за январь-июнь характеризуется следующими данными:
| Месяцы | Январь | Февраль | Март | Апрель | Май | Июнь |
| Задолженность, млн. руб. | 42, 0 | 52, 2 | 64, 3 | 51, 4 | 54, 6 | 52, 1 |
Для анализа динамики просроченной задолженности вычислите:
1) цепные и базисные абсолютные приросты, темпы роста и темпы прироста, абсолютное содержание одного процента прироста; полученные показатели представьте в таблице и постройте график;
2) средние показатели динамики просроченной задолженности по оплате труда;
Сделайте выводы.
Задача 27.
Динамика стоимости яиц куриных в РФ характеризуется следующими данными:
| Год | |||||||
| Цена за дес., руб. | 16, 57 | 24, 50 | 27, 06 | 34, 89 | 40, 02 | 34, 16 | 38, 56 |
Для анализа динамики стоимости яиц вычислите:
1) цепные и базисные абсолютные приросты, темпы роста и темпы прироста, абсолютное содержание одного процента прироста; полученные показатели представьте в таблице и постройте график;
2) средние показатели динамики стоимости яиц;
Сделайте выводы.
Задача 28.
Динамика стоимости сливочного масла в РФ характеризуется следующими данными:
| Год | |||||||
| Цена за кг, руб. | 69, 12 | 102, 42 | 109, 71 | 155, 10 | 175, 54 | 191, 68 | 239, 55 |
Для анализа динамики стоимости сливочного масла вычислите:
1) цепные и базисные абсолютные приросты, темпы роста и темпы прироста, абсолютное содержание одного процента прироста; полученные показатели представьте в таблице и постройте график;
2) средние показатели динамики стоимости сливочного масла;
Сделайте выводы.
Задача 29.
Динамика стоимости сахара-песка в РФ характеризуется следующими данными:
| Год | |||||||
| Цена за кг, руб. | 15, 62 | 19, 69 | 22, 71 | 21, 63 | 23, 07 | 33, 02 | 40, 62 |
Для анализа динамики стоимости сахара-песка вычислите:
1) цепные и базисные абсолютные приросты, темпы роста и темпы прироста, абсолютное содержание одного процента прироста; полученные показатели представьте в таблице и постройте график;
2) средние показатели динамики стоимости сахара-песка;
Сделайте выводы.
Задача 30.
Динамика стоимости подсолнечного масла в РФ характеризуется следующими данными:
| Год | |||||||
| Цена за литр, руб. | 23, 20 | 40, 06 | 39, 41 | 60, 26 | 74, 32 | 58, 06 | 72, 60 |
Для анализа динамики подсолнечного масла вычислите:
1) цепные и базисные абсолютные приросты, темпы роста и темпы прироста, абсолютное содержание одного процента прироста; полученные показатели представьте в таблице и постройте график;
2) средние показатели динамики стоимости подсолнечного масла;
Сделайте выводы.
Методические указания по решению задач:
Ряд динамики – это ряд последовательно расположенных статистических показателей (в хронологическом порядке), изменение которых показывает ход развития изучаемого явления.
Ряд динамики состоит из двух элементов: момента (периода) времени и соответствующего ему статис