
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Применение собственных значений матриц и собственных векторов в строительных расчетах. Постановка задачи и методы решения.
|
|
Явные и неявные схемы разностной аппроксимации сеточных уравнений. Их преимущества и недостатки. Алгоритм реализации явной схемы на примере решения уравнения теплопроводности.
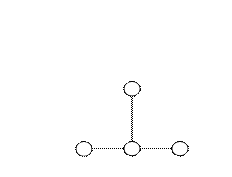 Явная схема:
Явная схема:
Ui, j+1
Ui-1, j Ui, j Ui+1, j
Устойчива только при λ < 1/2 или ԏ < =sqr(h)/2. Вычисления придется вести с очень малым шагом по времени. Число операций значительно меньше.
Неявная схема:
Ui-1, j+1 Ui, j+1 



 Ui+1, j+1
Ui+1, j+1
Ui, j
Устойчива при любых значениях параметра λ.
Алгоритм численного решения задачи теплопроводности следующий:
На нулевом временном слое j=0 решение известно из начального условия Ui, 0=f(xi), i=0, 1, …, n.
Также известны значения функции в левых и правых граничных узлах U0, j=мю1(tj); Un, j=мю2(tj);
В каждом следующем слое искомая функция определяется по формулам соответствующим явной и неявной схемам.
Для выполнения расчетов по разностным схемам важно такое их свойство, как устойчивость.
Применение собственных значений матриц и собственных векторов в строительных расчетах. Постановка задачи и методы решения.
2 группы алгоритма решения:
-итерационные методы
-методы преобразования подобия
В теории напряженного состояния тела, для тензоров напряжений собственные значения определяют главные норм-е напряжения, а собственными векторами задаются направления.
Собственные значения соответствуют собственным частотам колебаний. Позволяют определить критические нагрузки.
Собственные векторы характеризуют модули этих колебаний.
В общем виде задача на собственные значения форм-ся: AX= λ X, где А-матрица размерности n x n.
Требуется найти n скалярных значений λ и собственные векторы Х, соответствующие каждому из собственных значений.
|