
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Системи числення та кодування
|
|
Система числення – це спосіб запису чисел цифровими символами (цифрами) за певною сукупністю правил. У ЦТ використовується лише позиційна система числення, за якою значення кожної цифри, що входить у число, залежить від її місця розташування в записі цього числа. Кожна система числення має певний набір символів (цифр), кількість символів в якому відповідає основі даної системи числення. Позиція символу у зображенні числа називається розрядом.
У загальному випадку будь-яке число 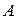 у позиційній системі числення з постійною основою
у позиційній системі числення з постійною основою  можна відобразити числовим рядом.
можна відобразити числовим рядом.
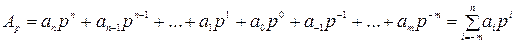 (1.1)
(1.1)
де 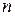 – число знаків до коми;
– число знаків до коми;  – число знаків після коми;
– число знаків після коми; 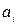 – число в і-му розряді;
– число в і-му розряді; 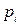 – вага і-го розряду.
– вага і-го розряду.
У десятковій системі числення 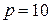 , оскільки набір цифр {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. У ЦТ для зображення числової інформації використовуються в основному десяткова, двійкова і шістнадцяткова системи числення.
, оскільки набір цифр {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. У ЦТ для зображення числової інформації використовуються в основному десяткова, двійкова і шістнадцяткова системи числення.
Двійкова система числення має набір цифр {0, 1}, тому 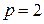 . Будь-яке число
. Будь-яке число  у двійковій системі числення можна зобразити виразом (1.1), який дає десятковий еквівалент. Наприклад,
у двійковій системі числення можна зобразити виразом (1.1), який дає десятковий еквівалент. Наприклад,
 .
.
Для практики корисно запам’ятати ваги перших 13 розрядів цифр двійкової системи чисел:
2 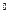 2
2 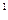 2
2 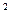 2
2 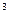 2
2 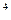 2
2  2
2 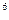 2
2 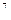 2
2 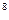 2
2  2
2 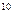 2
2 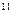 2
2 
1 2 4 8 16 32 64 128 256 512 1024 2048 4096
Шістнадцяткова система числення має набір цифр {0, 1,..., 9, А, В, С, D, Е, F}, тому 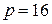 , де великими буквами латинського алфавіту зображені десяткові цифри відповідно 10, 11, 12, 13, 14, 15. Для будь-якого шістнадцяткового числа також легко знайти його десятковий еквівалент, якщо застосувати (1.1). Наприклад,
, де великими буквами латинського алфавіту зображені десяткові цифри відповідно 10, 11, 12, 13, 14, 15. Для будь-якого шістнадцяткового числа також легко знайти його десятковий еквівалент, якщо застосувати (1.1). Наприклад,
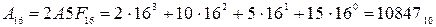
Корисно також запам’ятати такий ряд чисел:
16 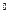 16
16 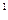 16
16 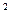 16
16 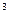 16
16 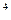 16
16 
1 16 256 4096 65536 1048576
Вісімкова система числення має набір цифр {0, 1,..., 6, 7} і, відповідно,  . Розглянуті системи числення порівняні у табл.1.
. Розглянуті системи числення порівняні у табл.1.
Таблиця 1.
| “2” | “8” | “10” | “16” |
0 0 0 0
1 1 1 1
10 2 2 2
11 3 3 3
100 4 4 4
101 5 5 5
110 6 6 6
111 7 7 7
1000 10 8 8
1001 11 9 9
1010 12 10 A
1011 13 11 B
1100 14 12 C
1101 15 13 D
1110 16 14 E
1111 17 15 F
10000 20 16 10
10001 21 17 11
......................................
11001 31 25 19
11010 32 26 1A
11011 33 27 1B
......................................
Систем числення може бути безліч. Поряд із згаданими системами у пристроях ЦТ можна зустріти й такі, як, наприклад, трійкова (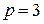 ). Очевидно, що вибір тої чи іншої системи числення залежить від певних критеріїв, які мають виконуватись для забезпечення оптимального результату.
). Очевидно, що вибір тої чи іншої системи числення залежить від певних критеріїв, які мають виконуватись для забезпечення оптимального результату.
Десяткова система числення, якою користуємось у повсякденному житті, не є найкращою з точки зору її технічної реалізації у цифрових пристроях. Відомі на сьогодні елементи, що мають десять стійких станів, щоб розрізнити всі десять символів (рівнів), наприклад, декатрони, мають невисоку швидкодію та складні для виготовлення. Отже, виникає закономірне питання: яка система числення найкраща? Вчені довели, що раціональною з точки зору мінімальних витрат умовного обладнання є система числення з основою 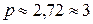 . Отже, трійкова система краща за двійкову? Однак з’ясувалося, що за такими характеристиками цифрових пристроїв, як швидкодія, об’єм пам’яті, техніка виконання арифметичних та логічних операцій, найкращою є двійкова система числення.
. Отже, трійкова система краща за двійкову? Однак з’ясувалося, що за такими характеристиками цифрових пристроїв, як швидкодія, об’єм пам’яті, техніка виконання арифметичних та логічних операцій, найкращою є двійкова система числення.
Розглянемо, чому крім десяткової та двійкової систем числення в цифровій схемотехніці використовуються ще й такі системи числення, як вісімкова, шістнадцяткова т.ін. Справа в тому, що якщо нас цілком влаштовує десяткова система, а для цифрового пристрою (мікропроцесорів, ЕОМ тощо) – виключно двійкова, бо там інформація обробляється тільки за допомогою нулів і одиниць, то проміжною, сполучною ланкою між нами і цифровим пристроєм має бути така система числення, яка була б найзручнішою як для взаємного переводу обох систем, так і для забезпечення простої технічної реалізації процедури. Для цього власне використовують поміжні системи числення – коди, за допомогою яких можна уникнути довгих ланцюжків з нулів та одиниць, які властиві двійковій системі. До таких систем кодування належить двійково-десятковий код (ДДК).
Особливість ДДК полягає в тому, що кожній десятковій цифрі даного розряду відповідав чотирибітове (група з чотирьох бітів) двійкове число – тетрада.Наприклад єднання двох тетрад дає можливість зобразити двозначне десяткове число, а з точки зору інформативності – реалізувати 16x16 – 256 двійкових комбінацій. При такому числі комбінацій можна закодувати не тільки 80 різних друкованих знаків клавіатури друкарської машинки, але й усі букви латинського алфaвіту розділові знаки, різні символи тощо. Перейти з десяткового числа до ДДК дуже просто. Наприклад:
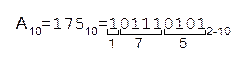
Але при перетворенні десяткових чисел ДДК має надлишковість, бо при групуванні тетрадами шість комбінацій відпадає. Водночас при групуванні тріадами (трьома бітами), навпаки, інформативність падає. Цей факт і пояснює зручність шістнадцяткової системи числення, бо для ДДК як раз і потрібно 16 бітових комбінацій, який повністю забезпечує одна тетрода (1111 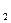 =15
=15 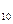 ). Зрозуміло, що при групуванні тріадами найзручнішою буде вісімкова система числення – там як раз вистачає 8 бітових комбінацій (111
). Зрозуміло, що при групуванні тріадами найзручнішою буде вісімкова система числення – там як раз вистачає 8 бітових комбінацій (111 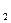 =7
=7 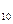 ).
).
Треба мати на увазі, що обидва коди – “16” і “8” – це тільки спосіб зображення двійкових чисел, якими оперують цифрові пристрої та мікропроцесори. Однак з точки зору інформатики код “16” має більші можливості, ніж код “8”. Перевага коду “16” над кодом “8” ще в тому, що мікропроцесори маніпулюють словами, які залежно від функціональних можливостей можуть мати набори з 4, 8, 16, або 32біт.
ДДК називають ще кодом 8-4-2-1, бо ці цифри відповідають вагам розрядів однієї тетради відповідно 2 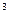 (старшого розряду), 2
(старшого розряду), 2 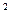 , 2
, 2 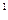 і 20 (молодшого розряду). До двійково-кодованої десяткової системи числення належать й інші системи кодування.
і 20 (молодшого розряду). До двійково-кодованої десяткової системи числення належать й інші системи кодування.
При синтезі таких комбінаційних цифрових пристроїв, як перетворювачі кодів, що призначені для перетворення одного коду в інший, необхідно мати дані про різновиди цих систем кодування.
У табл.2 зведені найбільш поширені в ЦТ різновиди позиційних кодів. До них належать ДЦК 8-4-2-1, код 2-4-2-1 (або код Айкена), код з лишком 3 (або код [8-4-2-1] + 3), код Грея та циклічний код Джонсона.
ДЦК 8-4-2-1, який утворений і зображеннями кожної десяткової цифри вагами 2 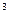 -2
-2 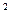 -2
-2 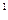 -2
-2 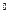 , є найбільш поширеним, тому його найчастіше застосовують для переводу в інший код.
, є найбільш поширеним, тому його найчастіше застосовують для переводу в інший код.
ДЦК з лишком 3 (8-4-2-1) + 3 застосовують для кодування декад при двійково-десятковому зображенні чисел. Особливістю цього коду є те, що всі тетради мають значення на три одиниці більше від тетради коду 8-4-2-1.
Таку властивість самодоповнення має код Айкена (2-4-2-1). Для цього коду ваги розрядів тетради відповідно дорівнюють 2 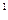 -2
-2 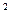 -2
-2 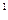 -2
-2 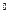 . Таблиця кодування, як видно з табл.2, поділяється на дві частини: 0-4 – це тетради, що повторюють еквіваленти; 5-9 – кожна тирада у ДЦК має лишок + 0110. Така властивість коду Айкена дозволяє довільну цифру одної частини таблиці перетворити на її доповнення до 9 простим інвертуванням.
. Таблиця кодування, як видно з табл.2, поділяється на дві частини: 0-4 – це тетради, що повторюють еквіваленти; 5-9 – кожна тирада у ДЦК має лишок + 0110. Така властивість коду Айкена дозволяє довільну цифру одної частини таблиці перетворити на її доповнення до 9 простим інвертуванням.
Особливе місце серед позиційних систем кодування посідають код Грея і циклічний код Джонсона. Це спеціальні коди, які мають непостійні ваги розрядів.Якщо у двійковому коді при переході від зображення одного числа до зображення наступного може відбуватись одночасна зміна цифр у кількох його розрядах, то в кодах Грея і Джонсона сусідні числа відрізняються цифрою (1 або 0) тільки в одному розряді. Така особливість цих кодів запобігає появі джерела помилки у роботі апаратури у тих випадках, коли здійснюється послідовний перехід (зміна) числа з одного такту в наступний (наприклад, від 6 до 5).
У циклічному коді Джонсона перехід до наступного числа здійснюється шляхом послідовної заміни 0 на 1 до заповнення всіх розрядів одиницями, а потім заміною 1 на 0 до заповнення нулями. Помилки за допомогою кода Джонсона виявляються тоді, коли у “хвилі нулів” цього коду з’являється одна або кілька одиниць, а в “хвилі одиниць” – відповідно один або кілька нулів.
Крім розглянутих існує безліч інших типів та різновидів кодів. Зокрема, для спрощення арифметичних операцій існують спеціальні арифметичні коди. До таких кодів належать обернений код числа 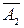 , який отримується простою зміною у цьому числі всіх нулів одиницями, а одиниць нулями, і доповняльний код двійкового числа
, який отримується простою зміною у цьому числі всіх нулів одиницями, а одиниць нулями, і доповняльний код двійкового числа 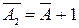 , який утворюється з оберненого
, який утворюється з оберненого 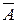 шляхом додавання одиниці до його молодшого розряду (див. табл.2).
шляхом додавання одиниці до його молодшого розряду (див. табл.2).
Таблиця 2
| Десят-кова цифра | ДДК 8-4-2-1 | ДДК 2-4-2-1 | ДДК 8-4-2-1 (+3) | Код Грея | Код Джон-сона | Обернений код двійко-вого числа | Доповняль-ний код двій-кового числа |
0 0000 0000 0011 0000 00000 11111 00000
1 0001 0001 0100 0001 10000 11110 11111
2 0010 0010 0101 0011 11000 11101 11110
3 0011 0011 0110 0010 11100 11100 11101
4 0100 0100 0111 0110 11110 11011 11100
5 0101 1011 1000 0111 11111 11010 11011
6 0110 1100 1001 0101 01111 11001 11010
7 0111 1101 1010 0100 00111 11000 11001
8 1000 1110 1011 1100 00011 10111 11000
9 1001 1111 1100 1101 00001 10110 10111
10 0001 0000 0001 0000 0001 0011 1111 00000 10101 10110
11 0001 0001 0001 0001 0001 0100 1110 10000 10100 10101
12 0001 0010 0001 0010 0001 0101 1010 11000 10011 10100
13 0001 0011 0001 0011 0001 0110 1011 11100 10010 10011
14 0001 0100 0001 0100 0001 0111 1001 11110 10001 10010
15 0001 0101 0001 1011 0001 1000 1000 11111 10000 10001
16 0001 0110 0001 1100 0001 1001 11000 01111 01111 10000
17 0001 0111 0001 1101 0001 1010 11001 00111 01110 01111
Арифметичні операції над двійковими числами виконуються за такими самими правилами, як і над десятковими. Однак з метою спрощення структури цифрових пристроїв для виконання арифметичних операцій (додавання, віднімання, множення, ділення) застосовують алгоритми, які не властиві для звичайної десяткової арифметики.
Окреме місце у ЦТ займає кодування алфавітно-цифрової інформації. Сюди належить текстова інформація, що являє собою послідовність алфавітно-цифрових символів, кожний з яких (буква, цифра, розділовий або математичний знак тощо) підлягає кодуванню. Щоб не було подвійного тлумачення, тобто щоб кожному символу відповідав тільки один код, застосовують спеціально призначені для цього стандартні коди. Зокрема, найчастіше в ЕОМ типу ІВМ застосовують код ASCII (American Standart Code of Information Interchange) – американський стандартний код обміну інформацією, де, наприклад, десятковому числу 1 відповідав код 00010000(2  ), числу 2 – код 00010001, числу 3 – код 00010010 тощо, а букві А – код 00011000, букві В – код 00011001, букві С – код 00011010 т.ін.
), числу 2 – код 00010001, числу 3 – код 00010010 тощо, а букві А – код 00011000, букві В – код 00011001, букві С – код 00011010 т.ін.
Наукове товариство ім.Т.Г.Шевченка у Львові з метою українізації комп’ютерів рекомендує дотримуватися кодування української абетки за кодовою таблицею USCII*, що гарантує хорошу сумісність програмного та інформаційного забезпечення персональних комп’ютерів типу ІВМ РС.
* Костирко В.С., Кульчицький І.М. Про кодування букв української абетки та програмне забезпечення для використання її на персональних комп’ютерах. – Львів; НТШ у Львові, 1990.