
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Комбінаційні суматори.
|
|
Це функціональні вузли, що здійснюють арифметичне підсумовування (додавання) чисел. У цифровій техніці технічні підсумовування виконуються в основному над двійковими (рідше над двійково-десятковими) числами (кодами). Додавання багаторозрядного слова за допомогою суматора здійснюється порозрядно з урахуванням переносу в сусідній старший розряд. Тому при побудові суматора необхідно враховувати не лише появу переносу в даному розряді, ала й можливість одерження аналогічного переносу від сусіднього молодшого розряду.
За принципом побудови і типом використання елементів розрізняють комбінаційні та накопичуючі суматори. Результати проміжного порозрядного додавання у накопичуючих суматорах зберігаються (запам’ятовуються) в елементарних комірках пам’яті (запам’ятовувачів), функцію яких використовують тригери. Комбінаційні суматори не мають “запам’ятовувачів”. У них додавання двійкових чисел здійснюється позиційним паралельним кодом одночасно. Як і у звичайних КП, результат на виході у комбінаційних суматорах зникає зразу після припинення дії вхідних сигналів. Тому до складу комбінаційних суматорів, як правило, входять вхідні та вихідні регістри, тобто пристрої, що здатні записувати чи перезаписувати проміжний результат підсумування у послідовному або паралельному коді.
Для додавання двійкових чисел можуть застосовуватись як одно-, так і багаторозрядні суматори, а сама процедура підсумування може здійснюватись або послідовно, починаючи з молодшого розряду, або паралельно, коли всі розряди чисел додаються одночасно. Важливою ознакою паралельного суматора є спосіб організації переносу при підсумовуванні. Розрізняють суматори з послідовним, паралельним (наскрізним) та груповим переносом.
Як послідовні, так і паралельні суматори будуються на основі комбінаційного однорозрядного суматора, що складається з напівсуматора.
Напівсуматор * – це пристрій (рис.4.1), що має два входи (для доданків 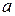 і
і  ) і два виходи (суми
) і два виходи (суми 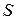 і переносу
і переносу  ), який призначений для виконання арифметичних дій за правилами, що наведені у табл.8. З таблиці істиності (табл.8) видно, що напівсуматор виконує елементарне додавання двох однорозрядних двійкових чисел та підсумовування отриманого результату з переносом у наступний старший розряд. Тому логічна структура напівсуматора має відображати стан обох виходів згідно виразами
), який призначений для виконання арифметичних дій за правилами, що наведені у табл.8. З таблиці істиності (табл.8) видно, що напівсуматор виконує елементарне додавання двох однорозрядних двійкових чисел та підсумовування отриманого результату з переносом у наступний старший розряд. Тому логічна структура напівсуматора має відображати стан обох виходів згідно виразами
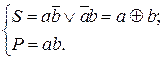 (4.1)
(4.1)
* Схемне позначення HS- з англ. Half Sum.

a) б)
Рис. 4.1.
Таблиця 8
| a | b | P | S |
Відповідно до наведених виразів логічна структура напівсуматора має містити два ЛЕ: суматор за модулем 2 і кон’юктор, що зображені на рис.4.1, б.
Однак у логіці роботи напівсуматора не передбачено переносу з сусіднього молодшого розряду, тому напівсуматор може здійснювати додавання тільки у молодшому розряді двійкових чисел. Поява одиниці переносу при додаванні двох розрядів (числа і переносу) дещо змінює правила підсумовування двійкових чисел. Такий одноразовий суматор потребує ще один (третій) вхід переносу з сусіднього молодшого розряду. Для цього служить так званий повний суматор.
Повний суматор (рис.4.2) реалізує процедуру додавання двох однорозрядних двійкових чисел з урахуванням переносу з молодшого розряду. Тому він має три входи (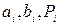 ) і два виходи (
) і два виходи (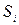 і
і 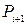 ). Логіка роботи повного суматора наведена у табл.9, де
). Логіка роботи повного суматора наведена у табл.9, де  ,
, 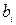 – доданки двійкових чисел в і - мурозряді;
– доданки двійкових чисел в і - мурозряді;  ,
, 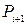 – переноси відповідно з молодшого розряду
– переноси відповідно з молодшого розряду 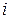 в сусідній старший розряд
в сусідній старший розряд 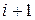 ;
; 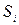 – утворена сума в і-му розряді.
– утворена сума в і-му розряді.
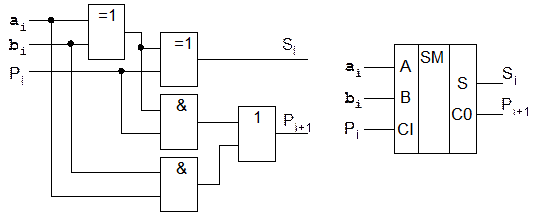
Рис 4.2.
Таблиця 9
| ai | bi | Pi | Pi+1 | Si |
Згідно з таблицею істиності (табл.9) робота повного суматора двійкових чисел описується такими логічними виразами:
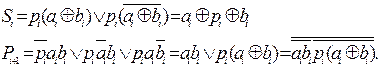 (4.2)
(4.2)
За виразами (4.2) тепер можна побудувати повний суматор, структурна схема та умовне позначення якого зображені на рис.3.4 (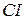 -вхід переносу, від англ. Carry Input,
-вхід переносу, від англ. Carry Input, 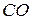 -вхід переносу, від англ. Carry Output).
-вхід переносу, від англ. Carry Output).
Для додавання двох n-розрядних двійкових чисел 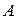 і
і 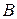 потрібно, очевидно, використати
потрібно, очевидно, використати 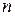 однорозрядних повних суматорів. При цьому можуть бути два способи підсумовування – послідовне і паралельне. Застосування того чи іншого принципу підсумовування залежить від характеру вводу/виводу чисел та організації переносів багаторозрядного суматора.
однорозрядних повних суматорів. При цьому можуть бути два способи підсумовування – послідовне і паралельне. Застосування того чи іншого принципу підсумовування залежить від характеру вводу/виводу чисел та організації переносів багаторозрядного суматора.
Послідовний суматор (рис.4.3, а) додає двійкові числа порозрядно, починаючи з молодшого розряду, з допомогою повного суматора. Утворений у даному розряді перенос 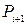 з допомогою схеми затримки (СЗ) затримується на один такт розряду і подається на вхід
з допомогою схеми затримки (СЗ) затримується на один такт розряду і подається на вхід  суматора у момент надходження наступного розряду доданків. Таким чином, завнтаженя доданків
суматора у момент надходження наступного розряду доданків. Таким чином, завнтаженя доданків 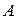 і
і 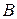 і їх підсумування відбувається з однаковою швидкістю: за один такт – один розряд, що забезпечує послідовне додавання чисел розряд за розрядом. Перевагою суматора послідовної дії є простота апаратурної реалізації, а недоліком – низька швидкодія.
і їх підсумування відбувається з однаковою швидкістю: за один такт – один розряд, що забезпечує послідовне додавання чисел розряд за розрядом. Перевагою суматора послідовної дії є простота апаратурної реалізації, а недоліком – низька швидкодія.
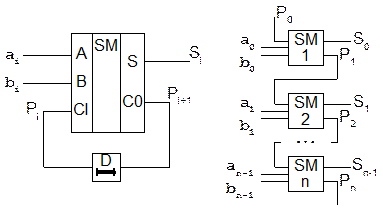
а) б)
Рис. 4.3
Паралельний суматор підсумовує два багатозначні числа одночасно по всіх розрядах і характеризується різними способами передачі переносів від молодших до старших розрядів. Якщо кожний біт переносу здійснюється послідовно з молодшого розряду до старшого, як це показано на рис.4.3, б, то такий паралельний суматор називають суматором з послідовним переносом. На вході переносу молодшого розряду 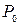 установлюють низький потенціал (тобто
установлюють низький потенціал (тобто  ), бо до нього не надходять інші сигнали переносів. У процесі послідовного проходження переносу в кожному розряді суматора встановлюється кінцеве значення суми. Очевидно, що протягом цього часу на входах суматора
), бо до нього не надходять інші сигнали переносів. У процесі послідовного проходження переносу в кожному розряді суматора встановлюється кінцеве значення суми. Очевидно, що протягом цього часу на входах суматора  і
і 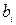 мають бути присутні сигнали, що відповідають кодам обох доданків. Отже, основна вимога до однорозрядного повного суматора – мінімальна затримка поширення ссигналу переносу. Хоч паралельний суматор з послідовним переносом на відміну від послідовного суматора більш швидкодіючий, однак, чим більше число розрядів мають доданки двійкових чисел, тим більша загальна затримка переносу старшого розряду.
мають бути присутні сигнали, що відповідають кодам обох доданків. Отже, основна вимога до однорозрядного повного суматора – мінімальна затримка поширення ссигналу переносу. Хоч паралельний суматор з послідовним переносом на відміну від послідовного суматора більш швидкодіючий, однак, чим більше число розрядів мають доданки двійкових чисел, тим більша загальна затримка переносу старшого розряду.
Для зменшення загальної затирмки застосовують принцип загального переносу, за яким вхідний перенос кожного розряду вибирається від переносу сусіднього молодшого розряду. Для цього застосовують спеціальні блоки (схеми) прискореного (наскрізного) переносу. Принцип прискореного переносу полягає у тому, що для кожного двійкового і-го розряду додатково утворюються два сигнали-переносу (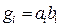 ) і поширення переносу (
) і поширення переносу ( ). Сигнал
). Сигнал 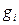 виробляється схемою тоді, коли в кожному і-му розряді перенос відбувається внаслідок комбінації доданків
виробляється схемою тоді, коли в кожному і-му розряді перенос відбувається внаслідок комбінації доданків  і
і 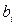 , а сигнал
, а сигнал  показує, передається отриманий у молодшому розряді сигнал переносу
показує, передається отриманий у молодшому розряді сигнал переносу  далі чи ні. Тому
далі чи ні. Тому 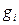 ще називають функцією генерації переносу, а
ще називають функцією генерації переносу, а 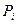 – функйією поширення переносу.
– функйією поширення переносу.
Процес формування прискореного переносу у паралельному суматорі описується логічним виразом, який випливає з виразу для 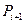 повного суматора:
повного суматора:
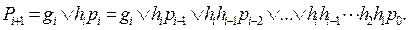 (4.3)
(4.3)
Хоч вираз для переносу досить складний, з нього очевидно, що біт переносу в довільному розряді суматора принципово може бути сформованим відразу, як тільки визначиться біт переносу у наймолодшому розряді. Таким чином, за рахунок ускладнення схеми суматора за принцмпом паралельного переносу досягається більша швидкодія процесу підсумовування, ніж при послідовному переносі.
Внаслідок великої складності побудови суматора з паралельним переносом для n-розрядних доданків його в чистому виді практично не застосовують. Однак принцип паралельного переносу використовується в поширених суматорах з так званим груповим (паралельно-паралельним) переносом.
Паралельний суматор з груповим переносом складається з n-розрядного суматора, що має 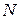 груп, в межах кожної з яких формування переносу здійснюється одночасно, без затримки від розряду до розряду. Вихід переносу від молодшої групи розрядів є одним з доданків для формування сигналу переносу в черговій старшій групі. Таким чином, затримка формування переносу на виході суматора буде визначатися сумарною затримкою формування переносів у
груп, в межах кожної з яких формування переносу здійснюється одночасно, без затримки від розряду до розряду. Вихід переносу від молодшої групи розрядів є одним з доданків для формування сигналу переносу в черговій старшій групі. Таким чином, затримка формування переносу на виході суматора буде визначатися сумарною затримкою формування переносів у 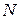 групах. Порівняно з суматором з паралельним переносом у чистому виді у суматора з груповим переносом досягається більша швидкодія за рахунок паралельного переносу між групами у поєднанні з паралельним переносом всередині групи. Це найбільш швидкодіючі суматори в діапазоні розрядності
групах. Порівняно з суматором з паралельним переносом у чистому виді у суматора з груповим переносом досягається більша швидкодія за рахунок паралельного переносу між групами у поєднанні з паралельним переносом всередині групи. Це найбільш швидкодіючі суматори в діапазоні розрядності  . Залежно від елементного базису, в якому побудована схема, величина затримки у такого суматора від розрядності не залежить. Цією перевагою доводиться розплачуватись значними елементними затратами. Тому паралельні суматори з груповим переносом застосовують там, де вимоги до високої продуктивності виконованої функції більші за вимоги щодо економічності пристрою.
. Залежно від елементного базису, в якому побудована схема, величина затримки у такого суматора від розрядності не залежить. Цією перевагою доводиться розплачуватись значними елементними затратами. Тому паралельні суматори з груповим переносом застосовують там, де вимоги до високої продуктивності виконованої функції більші за вимоги щодо економічності пристрою.