Diaognostic checking

Once a model is specified, it is likely to commit one or more of the following specification errors:

1. Omission of a relevant variables;

2. Inclusion of an unnecessary variable;

3. Adopting the wrong functional form;

4. Errors of measurements;

5. Incorrect specification of the stochastic error term.

There is a distinction between tests of specification and tests of mis-specification or diagnostic tests.

In a test of specification there is a clearly defined alternative hypothesis i.e. we have in mind the true model but somehow we do not estimate the correct model.

In contrast, in a test of mis-specification or diagnostic test we have no clearly defined alternative hypothesis, i.e. we do not know what the true model is to begin with.

Due to any one of the above specification errors, our parameter estimates will be biased, inconsistent and usual confidence interval and hypothesis testing are likely to unreliable and give misleading conclusions. Here we discuss some of the tests for specification errors.

The diagnostic tests are tests that are meant to diagnose a good model.

Tests for Omitted Variables

Consider the true linear regression model is

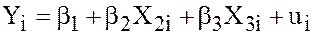(4)

But some reason, we omitting the variable 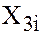and estimate the model

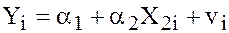(5)

Due to omitting the variable 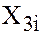, the error term in the mis-specified model will be 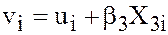. Due to this, the plot of the residuals will exhibit noticeable distinct pattern and one could observe significant Durbin-Watson statistics or positive correlation.

Our parameter estimates will be biased as well as inconsistent, the disturbance variance will be incorrect and usual confidence interval and hypothesis testing are likely to give unreliable and misleading conclusions.

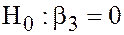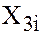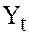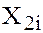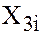Due to omitting the variable we test the hypothesis . If the data on are available, we have to regress on , and test whether the coefficient of 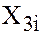is zero or not.

In case data on 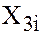are not available Ramsey suggests the use of RESET test, where , 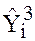are use as proxies for 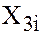i.e. we run the regression

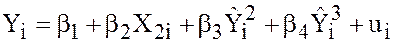a

(6)

obtained from (6) is denoted as 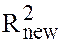and that from (5) is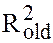

We carry out Wald F test (p522, eq. 8.5.18) for the omission of the variables. If the computed F test is significant, one could accept the hypothesis that the model is mis-specified.

Overfitting a Model

Let us assume that the true model is

(7)

But we commit the specification error by including the un-necessary variable 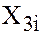and fit the following model

(8)

The consequences of this specification error are that the OLS parameter estimates will be inefficient though they are unbiased and consistent.

To test for unnecessary variables in the model, we can apply usual t-test and F-test; provided we have true model known.

Examination of Residuals and Model Fit

Residuals (error, disturbances) are typically analyzed in linear modelling with the goal of identifying poorly fitting values. If it is observed that there exist a sufficiently large number of these poorly fitting values, then often the linear fit is determined to be inappropriate for the data.

Examination of the residuals is a good visual diagnostic to detect autocorrelation or heteroscedasticity. However, if there are specification errors due to dynamic misspecification or incorrect functional form, the residuals will exhibit noticeable patterns.

In this case detection of positive autocorrelation by Durbin-Watson test statistics is a measure of specification error. Also significant values for the statistics designed to test for heteroskedasticity can also be indicative of mis-specification.

Other common use of residual include: looking for signs of nonlinearity, evaluating the effect of new explanatory variables, creating goodness of fit statistics, and evaluating leverage (distance from the mean) and influence (change exerted on the coefficient for individual data points.

Residuals from generalized linear models are often not normally distributed, and might have stochastic behaviour of the data, so we should have apply a wide range of graphical and inferential tools developed for the linear model to investigate potential outliers and other interesting behaviour.