
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Распределение скоростей и расход в ламинарном потоке
|
|
При ламинарном режиме слои жидкости движутся параллельно друг другу и скорость в любой точке потока не изменяется с течением времени. При ламинарном течении скорость максимальна на оси трубы, рис. 9.2, у ее стенок скорость равна нулю, т.к. частички жидкости прилипают к стенке, а к оси трубы скорости плавно нарастают. Эпюра распределения скоростей в сечении трубы представляет параболу второй степени и скорость на любом расстоянии 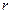 от оси трубы (
от оси трубы (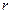 <
< 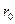 ) может быть определена по формуле
) может быть определена по формуле
u = 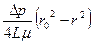 , (9.3)
, (9.3)
где 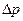 - перепад давления на длине
- перепад давления на длине 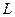 ; μ - динамический коэффициент вязкости;
; μ - динамический коэффициент вязкости; 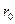 - радиус трубы;
- радиус трубы; 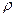 - плотность жидкости. Если к двум сечениям,
- плотность жидкости. Если к двум сечениям,
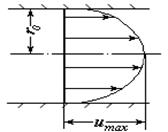
ограничивающим участок потока длиной 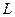 , применить уравнение Бернулли, то получим
, применить уравнение Бернулли, то получим
 hтр =
hтр = 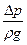 . (9.4)
. (9.4)
Возможно получить другое выражение для распределения скоростей, если выразить 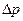 из (9.4) и подставить в (9.3):
из (9.4) и подставить в (9.3):
u = 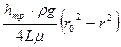 . (9.5)
. (9.5)
Рис. 9.2 Расход жидкости в трубе может быть определен по известной зависимости
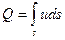 , (9.6) причем интегрирование производится по всей площади трубы, а в качестве u под интегралом – зависимость для скорости (9.3) или (9.5). В результате получается
, (9.6) причем интегрирование производится по всей площади трубы, а в качестве u под интегралом – зависимость для скорости (9.3) или (9.5). В результате получается
Q = 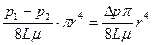 (9.7)
(9.7)
и выражение для средней скорости такое
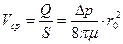 . (9.8)
. (9.8)
Иногда распределение скоростей необходимо получить, зная расход в трубе; для этого сравним (9.3) и (9.8) и получим
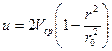 . (9.9)
. (9.9)
Приведенные выше зависимости получены аналитически и являются точными; такой подход и результаты возможны только для ламинарного режима.
Задача 9.3. Найти выражение для 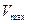 при ламинарном течении в круглой трубе; выразить
при ламинарном течении в круглой трубе; выразить 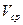 через
через 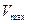 .
.