
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Измерительные сигналы и их преобразование
|
|
Измерительные сигналы – это сигналы, являющиеся физическими носителями измерительной информацию. К ним относятся: полезные сигналы, получаемые от исследуемых, контролируемых или управляемых объектов; вредные сигналы или помехи, поступающие в измерительную систему вместе с полезными сигналами или независимо от них; помехи, возникающие внутри измерительной системы; специально генерируемые в системе или вне ее сигналы, улучшающие работу системы (модуляция, дискретизация и др.).
Носителями физических сигналов используются импульсы механической, тепловой, электрической, магнитной, акустической и световой энергии и другие ее виды. Измерительные сигналы можно разделить на: постоянные и переменные; неслучайные и случайные; периодические, почти периодические, импульсные, стационарные и нестационарные. На рис.1.2. дана одна из возможных систем классификации сигналов.
Физические величины, как носители сигналов, подразделяются на непрерывные, имеющие бесконечно большое число размеров и дискретные во времени (рис.1.3, в). Соответственно, сигналы в зависимости от характера изменения во времени или пространстве делятся на непрерывные и дискретизированные (дискретные). Дискретизированные сигналы принимают отличные от нуля значения только в определенные моменты времени или в определенных точках пространства. На том же рис.1.3 даны примеры дискретизированных (рис.1.3, в) и квантованных (рис.1.3, б, г) сигналов.
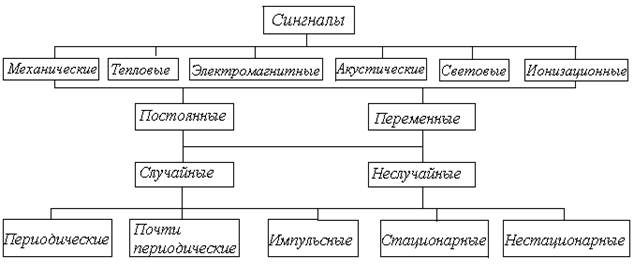
Рис. 1.2. Классификация сигналов
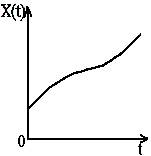
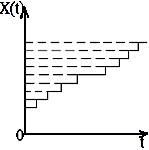
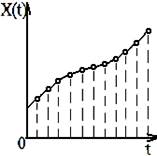
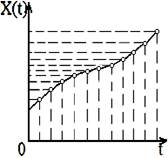
а) б) в) г)
Рис.1.3. Виды сигналов: а) аналоговый; б) квантованный; в) дискретизированный;
д) дискретизированно - квантованный
Во временной области измерительный сигнал рассматривается как функция времени, характеристики которой содержат информацию, заключенную в сигнале. Существует понятие типичные сигналы. Они подразделяются на импульсные и периодические.
Импульсным называется сигнал, величина которого ничтожно мала в любой точке временной оси, за исключением некоторой конечной области. Среди импульсных сигналов характерными являются (рис.1.4):

а) б) в)
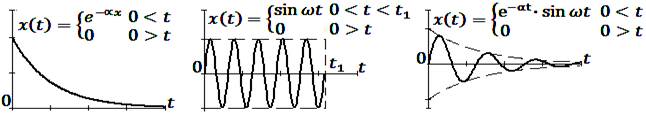
г ) д ) е )

ж) з) и)
Рис. 1.4. Импульсные сигналы
А – единичная функция, б – единичный импульс (d-функция Дирака), в – прямоугольный, г – экспоненциальный, д – пакет синусоид, е – затухающая синусоида, ж – гауссов импульс, з – импульс типа sin α t/t, и – импульс типа (sin α t/t) 2.
Информативными характеристиками и параметрами импульсных сигналов являются: величина сигнала как функция времени x (t); амплитудное (максимальное) значение max { x (t)}; длительность сигнала; период повторения; крутизна переднего 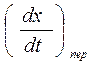 или заднего
или заднего  фронта; площадь под сигналом
фронта; площадь под сигналом
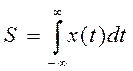 ,
,
энергия сигнала Е
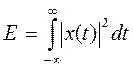 ,
,
Очевидно, площадь S для всех сигналов, кроме единичной функции (рис. 1.4, а), ограничена и конечна, а для единичного импульса (рис.1.4, б) и гауссова сигнала (рис. 1.4, ж) S =1.
Энергия всех сигналов на рис. 1.4, кроме показанных на рис. 1.4, а и б, конечна, поэтому можно написать
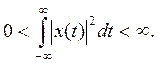
Сигналы, значения которых повторяются через постоянные интервалы времени, называются периодическими (рис. 1.5).
Для периодических сигналов справедливо соотношение
x(t)=x(t+kT), (k =0, ±1, ±2,..),
где Т - период сигнала.

Рис. 1.5. Периодические сигналы
Если известно поведение периодического сигнала за время Т, то полностью известно его прошлое и будущее. Поэтому такой сигнал несет мало информации. Однако его изучение необходимо потому, что, во-первых, знание реакции прибора на периодический сигнал позволяет получить многие свойства при его реакции на другие виды сигналов, а, во-вторых, периодический и, в частности, синусоидальный сигнал используется в качестве несущего, промодулированного полезным сигналом или помехой.
Синусоидальный сигнал (рис. 1.5. a,) для которого
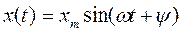
определяется тремя параметрами: амплитудой 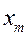 , частотой ω и фазой ψ. Любой из этих параметров при осуществлении амплитудной, частотной или фазовой модуляции может быть информативным.
, частотой ω и фазой ψ. Любой из этих параметров при осуществлении амплитудной, частотной или фазовой модуляции может быть информативным.
Периодический сигнал может быть представлен рядом Фурье
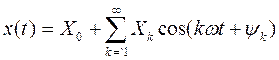
при этом параметры 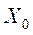 ,
,  ,
, 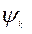 могут быть информативными. При
могут быть информативными. При
исследовании вибраций машин, аппаратов и устройств, периодические сигналы являются полезными измерительными сигналами (рис.1.5, б).
В измерительной технике широко применяются периодические последовательности прямоугольных импульсов, свойства которых определяются амплитудой 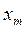 периодом повторения Т и длительностью τ (рис. 1.5. в, г). Применяются также пилообразные (рис.1.5, д) и треугольные (рис.1.5, е) импульсы.
периодом повторения Т и длительностью τ (рис. 1.5. в, г). Применяются также пилообразные (рис.1.5, д) и треугольные (рис.1.5, е) импульсы.
Для периодических сигналов рассматривают среднее значение за период
 ,
,
или
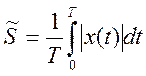 ,
,
и среднюю мощность
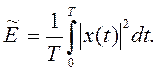
Очевидно, средняя мощность за период конечна, то есть
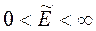 .
.
Сигнал, состоящий из конечного числа периодических составляющих, не имеющих кратного периода, называется почти периодическим. Многие полигармонические сигналы на практике являются почти периодическими.
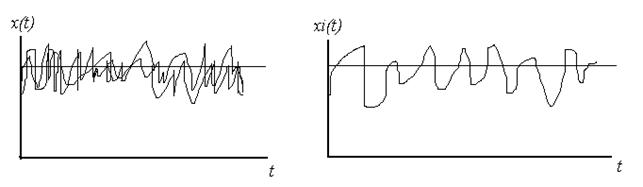
Особый класс составляют случайные сигналы, создаваемые случайными процессами в объектах и системах, о которых имеются неполные сведения. Случайные сигналы могут быть созданы посредством специальных генераторов. Характеристики случайных сигналов известны только с определенной вероятностью. Случайный сигнал х(t) полностью характеризуется бесконечным множеством реализаций, образующих ансамбль (рис. 1.6. а). Взятый из этого ансамбля отдельный сигнал 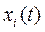 (рис. 1. 6, б) называется реализацией или выборочной функцией случайного сигнала х{t}.
(рис. 1. 6, б) называется реализацией или выборочной функцией случайного сигнала х{t}.
 |
 а) б)
а) б)
Рис. 1.6. Случайные сигналы
Рассмотрим характеристики сигналов в частотной области, с использованием преобразования Фурье. Периодический сигнал х(t) периода Т, удовлетворяющий условиям Дирихле (отсутствие разрывов второго рода), может быть разложен в ряд Фурье
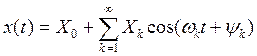 .
.
С помощью этого ряда периодический сигнал х(t) представлен в виде суммы бесконечно большого числа гармонических составляющих с амплитудами  , частотами
, частотами  и фазами
и фазами 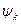 . Частоты гармоник кратны основной частоте, т. е.
. Частоты гармоник кратны основной частоте, т. е. 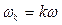 . При указанных выше условиях (условия Дирихле) ряд сходится, при этом чем выше порядок гармоники, тем меньше ее амплитуда. Совокупность амплитуд гармоник
. При указанных выше условиях (условия Дирихле) ряд сходится, при этом чем выше порядок гармоники, тем меньше ее амплитуда. Совокупность амплитуд гармоник 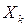 (k =0, 1, 2,...) характеризует свойства сигнала х (t) в частотной области и называется его спектром.
(k =0, 1, 2,...) характеризует свойства сигнала х (t) в частотной области и называется его спектром.
Обычно периодические сигналы имеют дискретные спектры, состоящие из отдельных линий. Такие спектры называются линейчатыми.
Чем короче во времени импульсный сигнал, тем шире его спектр. В предельном случае для единичного импульса δ (t) ширина спектра бесконечно велика. Сигнал, имеющий такой спектр, называется белым шумом.
Звенья измерительной системы осуществляют определенные преобразования сигналов. Характер преобразования определяется свойствами звеньев и описывается функцией преобразования
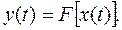
К числу основных операций преобразования относятся: квантование, дискретизация, восстановление, сравнение, функциональное изменение, фильтрация, модуляция, детектирование и запоминание. Преобразование может быть линейным и нелинейным. Звенья системы, осуществляющие линейные или нелинейные преобразования, называются соответственно линейными или нелинейными.
Для описания свойств системы можно воспользоваться дифференциальным уравнением, импульсной переходной функцией, передаточной функцией и частотной характеристикой. Знание одной из этих характеристик достаточно для получения всех остальных.
Преобразование непрерывного сигнала в дискретный, состоящий из множества квантов, называется квантованием по уровню. Дискретизация состоит в замене непрерывной по аргументу функции x(t) функцией x(ti) дискретного аргумента ti (рис.1.7). Шагом Тц дискретизации называется промежуток между соседними значениями аргумента.
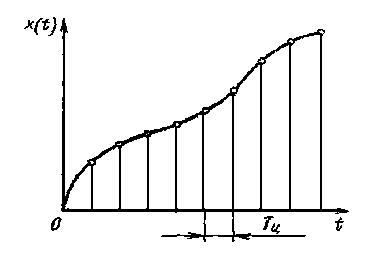
Рис. 1.7. Пример дискретизации сигнала
Дискретизация состоит в замене непрерывной по аргументу функции x (t) функцией 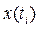 дискретного аргумента
дискретного аргумента  (рис.1.7). Шагом Тц дискретизации называется промежуток между соседними значениями аргумента. Дискретный сигнал как функция времени может быть представлен выражением:
(рис.1.7). Шагом Тц дискретизации называется промежуток между соседними значениями аргумента. Дискретный сигнал как функция времени может быть представлен выражением:

где δ — дельта-функция Дирака.
Дискретизация может быть равномерной, когда  , и неравномерной, если шаг
, и неравномерной, если шаг 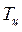 переменный. Реализация процесса дискретизации осуществляется, например, путем пропускания непрерывного сигнала х(t) через ключ, замыкаемый на очень короткое время в моменты
переменный. Реализация процесса дискретизации осуществляется, например, путем пропускания непрерывного сигнала х(t) через ключ, замыкаемый на очень короткое время в моменты 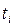 . При этом реализуется совокупность мгновенных значений
. При этом реализуется совокупность мгновенных значений  . По этим мгновенным значениям можно восстановить исходную функцию х(t) c необходимой точностью. Функцию, полученную в результате восстановления по отсчетам
. По этим мгновенным значениям можно восстановить исходную функцию х(t) c необходимой точностью. Функцию, полученную в результате восстановления по отсчетам 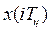 , называют восстанавливающей.
, называют восстанавливающей.
Операция выделения из спектра сигнала определенной полосы частот называется фильтрацией. Фильтрацию можно классифицировать по роду преобразованийна аналоговую и цифровую, а по расположению полос пропускания — на фильтрацию низких частот, высоких частот, полосовую и заграждающую.
Устройства, осуществляющие фильтрацию, называются фильтрами. Основной характеристикой фильтра является его частотная характеристика (коэффициент передачи), имеющая параметры: крутизну S=dk/dω и коэффициент затухания 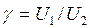 и, естественно, полосу пропускания (заграждения).
и, естественно, полосу пропускания (заграждения).
В целях увеличения крутизны фильтры делают многозвенными, а для уменьшения коэффициента затухания — активными. Существо последнего состоит в том, что пассивные звенья фильтра(ПФ)объединяют с операционными усилителями.
Цифровая фильтрация заключается в том, что сигнал х(t) пропускают через цифровой фильтр, в котором реализуется требуемая импульсная переходная функция h(t). В таком фильтре полоса пропускания определяется функцией h(t). Чем больше длительность h(t) во времени, тем уже полоса пропускания фильтра.
Обработанный, таким образом, дискретный сигнал затем пропускается через аналоговый низкочастотный фильтр, на выходе которого получают непрерывный сигнал у(t).
Воздействие измерительного сигнала х(t) на какой-либо стационарный сигнал называется модуляцией. В качестве стационарного сигнала, называемого носителем, выбирают синусоидальное колебание

Необходимость модуляции возникает, когда требуется повысить точность обработки измерительного сигнала, а также его передача на значительные расстояния.
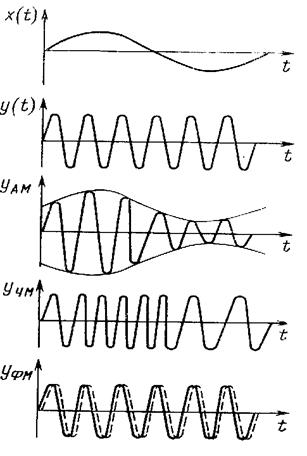
Рис. 1.8. Виды модуляции
Синусоидальное колебание определяется амплитудой уm, частотой ω и фазой 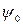 . Все эти три величины можно модулировать (рис. 1.8). В результате получаем амплитудную (АМ), частотную (ЧМ) и фазовую (ФМ) модуляции.
. Все эти три величины можно модулировать (рис. 1.8). В результате получаем амплитудную (АМ), частотную (ЧМ) и фазовую (ФМ) модуляции.
Модуляцию можно характеризовать как умножение модулируемой величины у(t) на множитель 1+mx(t) где х(t) — модулирующая функция, такая, что |x(t)|< 1, а т – глубина модуляции, причем 0< m < 1.
Выделение из модулированного сигнала составляющей, пропорциональной измеряемому сигналу, называется детектированием
Выделение полезной составляющей с частотой ω в продетектированном сигнале осуществляется с помощью низкочастотного фильтра.
Модулированное колебание состоит из несущей частоты и двух групп, называемых боковыми полосами. Если коэффициент частотной модуляции 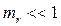 спектр частотно-модулированного сигнала не отличается от амплитудно-модулированного сигнала. Если условие
спектр частотно-модулированного сигнала не отличается от амплитудно-модулированного сигнала. Если условие 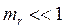 не выполняется (глубокая частотная модуляция), то спектр модулированного сигнала будет содержать не две боковых частоты, а множество частот. Поэтому спектр частотно-модулированного сигнала в общем случае шире, чем амплитудно-модулированного.
не выполняется (глубокая частотная модуляция), то спектр модулированного сигнала будет содержать не две боковых частоты, а множество частот. Поэтому спектр частотно-модулированного сигнала в общем случае шире, чем амплитудно-модулированного.
Детектирование ЧМ сигнала при 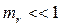 производится так же, как и детектирование АМ сигнала. При фазовой модуляции (см. рис. 1.8) модулирующий сигнал воздействует на несущее колебание. В сигнале информативным параметром является фаза. ЧМ и ФМ сигналы при указанных выше ограничениях совпадают. Различие же между ними состоит в том, что коэффициент ЧМ зависит от частоты Ω модулирующего сигнала, тогда как коэффициент ФМ не зависит от частоты. Это обстоятельство требует введения соответствующей коррекции сигнала после детектирования.
производится так же, как и детектирование АМ сигнала. При фазовой модуляции (см. рис. 1.8) модулирующий сигнал воздействует на несущее колебание. В сигнале информативным параметром является фаза. ЧМ и ФМ сигналы при указанных выше ограничениях совпадают. Различие же между ними состоит в том, что коэффициент ЧМ зависит от частоты Ω модулирующего сигнала, тогда как коэффициент ФМ не зависит от частоты. Это обстоятельство требует введения соответствующей коррекции сигнала после детектирования.
Детектирование ФМ сигнала может быть осуществлено так, как указано при рассмотрении АМ и ЧМ, при этом для получения фазы необходимо осуществить интегрирование  .
.
Если модулирующий сигнал х(t) имеет разрывы непрерывности первого рода, то для детектирования приходится применять фазочувствительные детекторы с использованием опорного сигнала.
Если в качестве модулируемого сигнала используется периодическая последовательность импульсов (рис. 1.9), то получим импульсную модуляцию.
При этом имеем амплитудную импульсную (АИМ), частотно-импульсную (ЧИМ), фазо-импульсную (ФИМ) и широтно-импульсную (ШИМ) модуляции.
Детектирование импульсных модулированных сигналов осуществляется посредством низкочастотных фильтров.
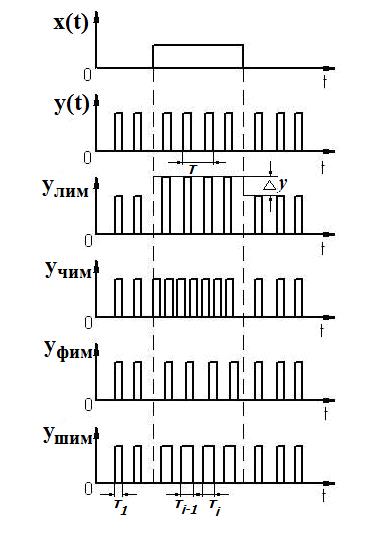
Рис. 1.9. Виды импульсной модуляции
В измерительной технике модуляция применяется не только для
более совершенной обработки измерительных сигналов, но также для фильтрации помех, которые модулируются несущими частотами, отличными от несущей полезного сигнала.
Параметры окружающей среды, режима полёта, параметры работы двигателя, агрегатов и систем летательного аппарата имеют различную природу образования. Посредством датчиков необходимые параметры преобразуются в электрический сигнал. В то же время выходной сигнал авиационных приборов на современных летательных аппаратах, как правило, имеет цифровой характер. Требуемая точность, надёжность и информативность измеренного сигнала может быть обеспечена применением высокоточных датчиков, а также посредством соответствующих видов преобразований.