Темы курсовых работ

По курсу «Моделирование»

1. Разработать программу для решения эллиптического уравнения

U_xx+U_yy=0, используя метод Либмана, для следующих условий:

x (0, 1), y (0, 1);

при x=0, граничное значение U(0, y) изменяется линейно от значения 0 до 10; на остальных значениях граничное значение равно нулю.

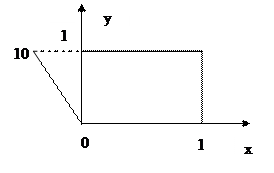Результат получить с точностью до 10^-6.

Для визуализации решения в виде изолиний разработать программный модуль.

2. Разработать программу для решения эллиптического уравнения

U_xx+U_yy=0, используя метод Либмана, для следующих условий:

x (0, 2), y (0, 1);

при x=0, граничное значение U(0, y) изменяется:

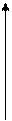
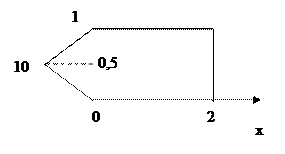На остальных значениях граничное значение равно нулю.

Результат получить с точностью до 10^-6.

Для визуализации решения в виде изолиний разработать программный модуль.

3. Разработать программу для решения эллиптического уравнения

U_xx+U_yy=0, используя метод Либмана, для следующих условий:

x (0, 10), y (0, 10);

граничное значение изменяется:

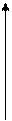
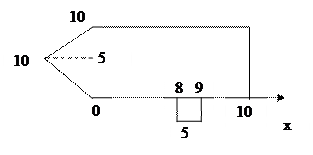На остальных значениях граничное значение равно нулю.

Результат получить с точностью до 10^-6.

Для визуализации решения в виде изолиний разработать программный модуль.

4. Разработать программу для решения эллиптического уравнения

U_xx+U_yy=0, используя метод Либмана, для следующих условий:

x (0, 8), y (0, 10);

граничное значение изменяется:

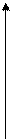
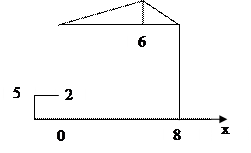На остальных значениях граничное значение равно нулю.

Результат получить с точностью до 10^-6.

Для визуализации решения в виде изолиний разработать программный модуль.

5. Разработать программу для решения эллиптического уравнения

U_xx+U_yy=0, используя ускоренный метод Либмана, для следующих условий:

x (0, 1), y (0, 1);

при x=0, граничное значение U(0, y) изменяется:

На остальных значениях граничное значение равно нулю.

Результат получить с точностью до 10^-6.

Для визуализации решения в виде изолиний разработать программный модуль.

6. Разработать программу для решения эллиптического уравнения

U_xx+U_yy=0, используя ускоренный метод Либмана, для следующих условий: x (0, 2), y (0, 1);

при x=0, граничное значение U(0, y) изменяется:

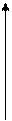
На остальных значениях граничное значение равно нулю.

Результат получить с точностью до 10^-6.

Для визуализации решения в виде изолиний разработать программный модуль.

7. Разработать программу для решения эллиптического уравнения

U_xx+U_yy=0, используя ускоренный метод Либмана, для следующих условий: x (0, 10), y (0, 10);

граничное значение изменяется:

На остальных значениях граничное значение равно нулю.

Результат получить с точностью до 10^-6.

Для визуализации решения в виде изолиний разработать программный модуль.

8. Разработать программу для решения эллиптического уравнения

U_xx+U_yy=0, используя ускоренный метод Либмана, для следующих условий:

x (0, 8), y (0, 10);

граничное значение изменяется:

На остальных значениях граничное значение равно нулю.

Результат получить с точностью до 10^-6.

Для визуализации решения в виде изолиний разработать программный модуль.

9. Разработать программу для решения эллиптического уравнения

U_xx+U_yy=0, используя метод прогонки по строкам, для следующих условий: x (0, 1), y (0, 1);

при x=0, граничное значение U(0, y) изменяется:

На остальных значениях граничное значение равно нулю.

Результат получить с точностью до 10^-6.

Для визуализации решения в виде изолиний разработать программный модуль.

10. Разработать программу для решения эллиптического уравнения

U_xx+U_yy=0, используя метод прогонки по строкам, для следующих условий: x (0, 2), y (0, 1);

при x=0, граничное значение U(0, y) изменяется:

На остальных значениях граничное значение равно нулю.

Результат получить с точностью до 10^-6.

Для визуализации решения в виде изолиний разработать программный модуль.

11. Разработать программу для решения эллиптического уравнения

U_xx+U_yy=0, используя метод прогонки по строкам, для следующих условий: x (0, 10), y (0, 10);

граничное значение изменяется:

На остальных значениях граничное значение равно нулю.

Результат получить с точностью до 10^-6.

Для визуализации решения в виде изолиний разработать программный модуль.

12. Разработать программу для решения эллиптического уравнения

U_xx+U_yy=0, используя метод прогонки по строкам, для следующих условий: x (0, 8), y (0, 10);

граничное значение изменяется:

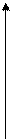
На остальных значениях граничное значение равно нулю.

Результат получить с точностью до 10^-6.

Для визуализации решения в виде изолиний разработать программный модуль.

13. Разработать программу для решения параболического уравнения

U_xx+U_t=0, используя явную схему, для следующих условий: x (0, 10), t (0, 100);

граничное значение: U(0, t)=100; U(10, t)=200;

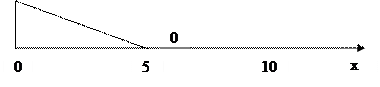Результат получить с точностью до 10^-6.

14. Разработать программу для решения параболического уравнения

U_xx+U_t=0, используя явную схему, для следующих условий: x (0, 10), t (0, 100);

граничное значение: U(0, t)=100; U(10, t)=200;

Результат получить с точностью до 10^-6.

15. Разработать программу для решения параболического уравнения

U_xx+U_t=0, используя явную схему, для следующих условий: x (0, 10), t (0, 100);

граничное значение: U(0, t)=100; U(10, t)=200;

начальное условие

Результат получить с точностью до 10^-6.

16. Разработать программу для решения параболического уравнения

U_xx+U_t=0, используя явную схему, для следующих условий: x (0, 10), t (0, 100);

граничное значение: U(0, t)=100; U(10, t)=200;

начальное условие

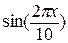
Результат получить с точностью до 10^-6.

17. Разработать программу для решения параболического уравнения

U_xx+U_t=0, используя неявную схему, для следующих условий:

x (0, 10), t (0, 100);

граничное значение: U(0, t)=100; U(10, t)=200;

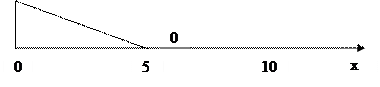Результат получить с точностью до 10^-6.

18. Разработать программу для решения параболического уравнения

U_xx+U_t=0, используя неявную схему, для следующих условий:

x (0, 10), t (0, 100);

граничное значение: U(0, t)=100; U(10, t)=200;

Результат получить с точностью до 10^-6.

19. Разработать программу для решения параболического уравнения

U_xx+U_t=0, используя неявную схему, для следующих условий:

x (0, 10), t (0, 100);

граничное значение: U(0, t)=100; U(10, t)=200;

начальное условие

Результат получить с точностью до 10^-6.

20. Разработать программу для решения параболического уравнения

U_xx+U_t=0, используя неявную схему, для следующих условий:

x (0, 10), t (0, 100);

граничное значение: U(0, t)=100; U(10, t)=200;

начальное условие

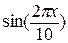
Результат получить с точностью до 10^-6.

21. Разработать программу для решения гиперболического уравнения

U_xx+U_tt=0, для следующих условий: x (0, 10), t (0, 50);

граничное значение: U(0, t)= U(10, t)= 0;

начальное условие

U(x, 0)=U(x, 1)=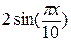

Результат получить с точностью до 10^-3.

22. Разработать программу для решения гиперболического уравнения

U_xx+U_tt=0, для следующих условий: x (0, 10), t (0, 50);

граничное значение: U(0, t)= U(10, t)= 0;

начальное условие

U(x, 0)=U(x, 1)=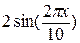

Результат получить с точностью до 10^-4.

23. Разработать программу для решения гиперболического уравнения

U_xx+U_tt=0, для следующих условий: x (0, 10), t (0, 50);

граничное значение: U(0, t)= U(10, t)= 0;

начальное условие

U(x, 0)=U(x, 1)=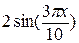

Результат получить с точностью до 10^-4.

24. Разработать программу для решения гиперболического уравнения

U_xx+U_tt=0, для следующих условий: x (0, 10), t (0, 50);

граничное значение: U(0, t)= U(10, t)= 0;

начальное условие

U(x, 0)=U(x, 1)=

Результат получить с точностью до 10^-4.