
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Замыкание модели трансформации вихря
|
|
Проблема создания более эффективных и экономичных энергетических установок неразрывно связана с развитием методов математического моделирования сложных турбулентных течений. Одним из таких методов является метод расчета труб с локальными завихрителями, в основе которого лежит модель трансформации вихря [1].
В систему основных расчетных уравнений модели входят осредненные интегральные уравнения сохранения импульса, потока вихря и энергии, полученные на основе пространственно осредненных дифференциальных уравнений при использовании параметрического описания компонент скорости, а также замыкающие феноменологические соотношения для определения компонент тензора сопротивления и скоростного формпараметра модели.
В настоящей работе для описания скоростного формпараметра предлагается использовать физическую гипотезу, основанную на результатах исследований, проведенных под руководством И.И. Новикова [2, 3], в которых было показано, что критическая скорость поступательного движения закрученного потока вязкой несжимаемой жидкости равна скорости распространения длинных центробежных волн. Предполагая, что при достижении режима гидродинамической стабилизации потока в протяженных каналах со спиральными завихрителями средняя расходная скорость потока соответствует критической скорости продольного движения, а взаимосвязь продольного и радиального градиентов давления определяет автомодельную форму профиля окружной скорости, что характерно для существования крупномасштабной вихревой структуры потока, можно получить замыкающее соотношение для определения скоростного формпараметра модели трансформации вихря q в следующем виде:
 , (1)
, (1)
где  – средняя расходная скорость в канале;
– средняя расходная скорость в канале; 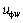 – тангенциальная «скорость скольжения» закрученного потока на стенке.
– тангенциальная «скорость скольжения» закрученного потока на стенке.
Ввиду отсутствия в доступной авторам литературе экспериментальных данных по измерению профилей скорости в каналах со спиральными завихрителями, сравнение расчетов по уточненной модели с результатами экспериментов проводилось относительно интегральных параметров, в частности, рассматривалось гидравлическое сопротивление каналов.

Рис.1. Зависимость коэффициента гидравлического сопротивления от числа Рейнольдса [4].
Экспериментальные данные получены на воде для труб со спиральным оребрением различной геометрии (Q – угол закрутки спирали; e = 2h/dвн – степень загромождения канала, где h – высота выступов, dвн – внутренний диаметр канала, m – заходность спирали)
Представленные на рис.1 иллюстрации демонстрируют хорошее совпадение расчетных кривых с экспериментальными данными для случаев различного загромождения проходного сечения канала.
Работы в области моделирования закрученных потоков выполняются при поддержке Минобразования РФ – грант ТОО-1.2-1252 № 01.200 102616.
Список литературы
1. Mitrofanova O.V., Korsun A.S., Saphronov A.V. Application of Transformation Vortex Model for Description of Swirl Flows in the Channels // 2nd European Thermal-Sciences and 14 UIT Nation. Heat Transfer Conference, Rome, Italy, May 29-31, 1996. V.1. Р.161-169.
2. Новиков И.И., Борзяк А.Н. Экспериментальное исследование поступательно-вращательного течения вязкой несжимаемой жидкости в цилиндрической трубе // Измерительная техника, 1966. № 12. С.15-20.
3. Новиков И.И., Скобелкин В.И., Абрамович Г.Н., Клячко Л.А. Закономерность расхода жидкости в закрученном потоке (эффект максимального расхода закрученного потока жидкости) – открытие № 389 внесено в Гос. реестр открытий 18.10.1990.
4. Мигай В.К. Повышение эффективности современных теплообменников. Л.: Энергия, 1980. 144 с.