
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Очень тривиальный пример
|
|
То, что при умножении 777 на 111 получается 86 247 — это очень тривиальный арифметический факт. Он может быть записан в виде равенства. Он может также считаться очень тривиальной теоремой из теории натуральных чисел.
Понимаю ли я это тривиальное высказывание?
И да, и нет. Конечно, я понимаю это утверждение — особенно когда вижу его написанным, так как в противном случае я, может быть, не справился бы с таким большим числом, как 86 247, или не смог бы его запомнить. (Я провел эксперимент и перепутал это число с числом 86 427.) В каком-то смысле я, конечно, сразу же понимаю его, как только услышу: числа 777 и 111 легко держать в уме, и я понимаю, что данное высказывание предлагается в качестве решения проблемы «какое число в десятичной системе равно произведению 777 и 111»?
Что же касается решения этой проблемы, я, конечно, знаю, что многие люди с легкостью могут решить ее в уме; может быть, и я справился бы с этим, если бы очень постарался. Однако если я хочу быть уверен в своем результате или хотя бы в том, что не спутаю его через минуту с другим результатом, мне придется прибегнуть к тому, что Бриджмен
называет «операцией с карандашом и бумагой»: мне придется оформить все это в виде алгоритма, состоящего из структурных единиц, с которыми легко работать. (Конечно, это — структурные единицы третьего мира). Одна из целей этого — устранение ошибок: общепринятые операции с карандашом и бумагой облегчают нахождение и устранение ошибок.
Пока мы использовали три из четырех объектов, входящих в мою схему решения проблем (схема Р 1—► ТТ —> ЕЕ —► Pi, предложенная в разделе 6). Для того, чтобы понять то или иное высказывание или некоторую пробную теорию, мы прежде всего спрашиваем: в чем состоит проблема? И чтобы устранить ошибки, мы производим вычисления с помощью карандаша и бумаги. Хотя мы начали с высказывания или пробной теории (ТТ), от них мы перешли к лежащей в их основе проблеме (к Pi), а затем — к методу вычисления, рассчитанному на устранение ошибок (ЕЕ). Присутствует ли здесь и вторая проблема (Р2)? Присутствует: метод устранения ошибок действительно приводит к смещению проблемы: в нашем случае — к очень тривиальному, регрессивному смещению — к замене одной задачи на умножение тремя более простыми задачами на умножение и одной задачей на сложение. Конечно, смещение проблемы от Р 1к Pi — регрессивное; это очевидно потому, что рассматриваемая нами проблема не представляет для нас реального теоретического интереса — мы просто применяем рутинную процедуру, цель которой — облегчить работу по решению проблемы и упростить проверку полученного результата (то есть обеспечить устранение ошибок).
Даже в этом весьма тривиальном примере можно различить разные степени понимания:
(1) Голое понимание того, что было сказано, — понимание в том смысле, в каком мы можем «понять» высказывание «777 умножить на 111 равняется 68427», не осознавая, что это неверно.
(2) Понимание того, что это высказывание — решение некоторой проблемы.
(3) Понимание этой проблемы.
(4) Понимание того, что это решение верно: в данном случае это тривиально просто.
(5) Проверка истинности высказывания при помощи того или иного метода устранения ошибок, в нашем случае опять-таки тривиального.
Есть, конечно, и другие степени понимания. В особенности пункт (3) — понимание проблемы — можно уточнять и далее. Действительно, кто-то может понять, а кто-то может и не понять, что эта проблема является вербальной, поскольку, хотя выражение «777 умножить на 111» и не десятичная запись, но этот способ записи ничуть не хуже, а может быть, и лучше, чем выражение «8 умножить на 10 000 плюс 6 умножить на 1000, плюс 2 умножить на 100, плюс 4 умножить на 10, плюс 7», и что «86 247» — это просто краткий способ записи этого последнего выражения. Понимание такого рода являет собой пример попытки понять фон проблемы, над которым обычно не задумываются. Таким образом, оно позволяет обнаружить проблему внутри этого фона.
Эти степени понимания17), конечно, как правило, нельзя выстроить в линейном порядке; почти в каждой точке возможны новые ответвления к дальнейшему, более глубокому пониманию, особенно в менее тривиальных случаях.
Таким образом, мы многое узнали из нашего простого примера. Может быть, из того, что мы смогли здесь узнать, важнее всего следующее. Каждый раз, когда мы пытаемся интерпретировать или понять теорию или высказывание, даже такое тривиальное, как обсуждавшееся здесь равенство, мы на самом деле поднимаем проблему понимания, и это всегда оказывается проблемой о проблеме, то есть проблемой более высокого уровня.
9. Случай объективного исторического понимания|8)
Все это верно для всех проблем понимания, особенно для проблемы исторического понимания. Моя гипотеза состоит в том, что основная задача всякого исторического понимания — гипотетическое воссоздание исторической проблемной ситуации.
Я попытаюсь подробнее объяснить этот тезис с помощью еще одного примера: с помощью нескольких исторических соображений по поводу теории Галилея о приливах. Эта теория оказалась «неудачной» (потому что она отрицает какое-либо влияние Луны на приливы), и даже в наше время Галилей подвергался жестоким нападкам личного характера за то, что упорно и догматично придерживался этой очевидно неверной теории.
Вкратце, теория Галилея утверждает, что приливы возникают в результате ускорения, которое, в свою очередь, возникает из-за сложного
17) Дильтей часто и справедливо подчеркивал, что существуют степени понимания. Однако я не вполне уверен, что он всегда различал степени понимания (то есть глубину или полноту понимания) и уверенность ('Sicherheit') в понимании, а уверенность в понимании, по моему представлению, — совсем другое и совершенно ошибочное понятие. Так, Дильтей замечает: «Наивысшая степень уверенности достигается в области интерпретации [объектов] научного ума» (Dilthey W. Gesammelte Schriften. Band 7. S. 260.) Мне кажется, что здесь что-то спутано. Или, может быть, я недопонимаю это высказывание? Что высокая степень уверенности в понимании может совмещаться с исключительно низкой степенью понимания, станет ясно, если задуматься над следующей формулировкой, содержащейся в книге: Сагпар Я. Introduction to Semantics. 1942. P. 22: «...понимать предложение, знать, что в нем утверждается, — то же самое, что знать, при каких условиях оно было бы истинным.» На самом деле я знаю, что равенство «777 умножить на 111 равняется 86 427» было бы верно в точности при том условии, если бы 777 умножить на 111 действительно равнялось 86 427. (На самом деле это не так). Я знаю это из определения истинности Тарского; и я знаю о всяком высказывании, что для него выполняется такое условие истинности. Получается, что я понимаю с уверенностью всякое высказывание, если только понимаю соответствующий язык, а это верно даже для исключительно низкой степени понимания, которую вряд ли имели в виду Дильтей или Карнап в своих теориях.
18) В оставшейся части этой главы я попытаюсь прошыюстрировать — в связи с проблемами исторического понимания — превосходство относящегося к третьему миру метода критической реконструкции проблемных ситуаций над относящимся ко второму миру методом интуитивного переживания заново некоторого личного опыта (ограниченным и субъективным, но в то же самое время наводящим (суггестивным) методом, без которого нельзя обойтись и ценность которого я не собираюсь отрицать).
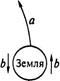
движения Земли. Точнее, когда равномерно вращающаяся Земля еще и движется вокруг Солнца, скорость точки земной поверхности, находящейся в данный момент на противоположной Солнцу стороне Земли, будет больше, чем скорость той же самой точки, когда через 12 часов она окажется на обращенной к Солнцу стороне. (Поскольку, если а — скорость движения Земли по орбите, а Ь — скорость вращения точки на экваторе, то а + Ь — это скорость этой точки в полночь, а а - Ь — ее скорость в полдень.) Таким образом, скорость изменяется, а это означает, что должны возникать периодические ускорения и замедления. Но всякие периодические ускорения и замедления таза с водой, говорит Пшилей, приводят к явлениям, напоминающим приливы. (Теория Галилея правдоподобна, но некорректна в приведенной форме: помимо постоянного ускорения, вызванного вращением Земли, то есть центростремительного ускорения, которое возникает и в том случае, когда а равно нулю, не возникает больше никаких ускорений и, следовательно, в частности, никаких периодических ускорений хэ\)

Что можно сделать, чтобы улучшить наше историческое понимание этой теории, которую так часто понимали неправильно? Мое решение этой проблемы понимания (которую я обозначу как «Pw» ♦) идет приблизительно в том же направлении, что и мое решение вопроса о понимании, обсуждавшееся ранее в связи с нашим тривиальным арифметическим уравнением.
Я утверждаю, что первый и наиважнейший шаг состоит в том, чтобы спросить: пробным решением какой проблемы (третьего мира) была теория Галилея? И в какой ситуации — логической проблемной ситуации — эта проблема возникла?
Проблема Галилея состояла просто-напросто в том, чтобы объяснить возникновение приливов. А вот с проблемной ситуацией дело обстоит далеко не так просто.
19) Можно сказать, что кинетическая теория Галилея о приливах противоречит так называемому принципу относительности Галилея, но такая критика была бы неверна как теоретически, так и исторически, поскольку этот принцип не относится к вращательному движению. Интуитивная физическая догадка Галилея о том, что вращение Земли имеет не-релягивистские механические последствия, правильна; и хотя эти последствия (движение волчка, маятник Фуко и т.д.) не объясняют возникновение приливов, сила Кориолиса, во всяком случае, оказывает на них некоторое воздействие. Более того, мы получим (небольшие) кинетические ускорения, как только учтем кривизну движения Земли вокруг Солнца.
* Индекс «u» — от англ. «understanding» («понимание»), — Прим. пер.
Ясно, что Галилея непосредственно интересовало даже не то, что я сейчас назвал его проблемой. К проблеме приливов его привела другая проблема: проблема истинности или ложности теории Коперника — проблема, движется ли Земля или находится в состоянии покоя. Галилей надеялся, что сможет использовать успешную теорию приливов в качестве решающего аргумента в пользу теории Коперника.
То, что я назвал проблемной ситуацией Галилея, оказывается сложным делом. Нельзя не признать, что проблема приливов вытекает из этой проблемной ситуации, но в специфической роли: объяснение приливов должно служить пробным камнем для теории Коперника. Однако и этого замечания недостаточно для понимания проблемной ситуации Галилея. Ведь пробная теория Галилея не просто пыталась объяснить изменения приливов: она пыталась объяснить их на определенном фоне, да еще и в рамках определенного заданного теоретического каркаса (framework). В то время, как фон для Галилея не представлял проблем, «галилеевский каркас», как я предлагаю его называть, был весьма проблематичен, и Галилей полностью осознавал этот факт.
В результате для решения нашей проблемы понимания (Ри) необходимо исследовать довольно сложный объект третьего мира. Объект состоит из проблемы приливов (пробным решением которой была теория Галилея) вместе с сопутствующими обстоятельствами — ее фоном и ее каркасом: этот сложный объект я и называю проблемной ситуацией.
Проблемную ситуацию Галилея можно охарактеризовать следующим образом. Галилея — как истинного космолога и теоретика — давно привлекала невероятная дерзость и простота главной идеи Коперника — идеи, что Земля и другие планеты являются лунами Солнца. Объяснительная мощь этой дерзкой идеи была очень велика, а когда Галилей обнаружил луны Юпитера и увидел в них уменьшенную модель солнечной системы, он счел это эмпирическим подкреплением этой дерзкой концепции, несмотря на ее весьма спекулятивный и почти априорный характер. Вдобавок ко всему этому ему удалось проверить на опыте выводимое из теории Коперника предсказание: оно состояло в том, что у внутренних планет должны быть фазы, как у Луны, и Галилею удалось наблюдать фазы Венеры.
Теория Коперника, как и теория Птолемея, была по существу геометрической космологической моделью, построенной геометрическими (и кинетическими) средствами. Но Галилей был физиком, и он знал, что настоящая проблема состоит в том, чтобы найти механическое (или, может быть, транс-механическое) физическое объяснение. Он действительно открыл некоторые из элементов такого объяснения, в частности законы инерции и соответствующий закон сохранения для вращательного движения.
Галилей дерзко пытался построить свою физику только на этих двух законах сохранения, хотя он вполне отдавал себе отчет в том, что в его физических знаниях наверняка имеются большие пробелы с точки зрения третьего мира. С точки зрения метода Галилей был совершенно прав, (171:) пытаясь объяснить все интересующие его явления на этой очень узкой основе; ведь только пытаясь по возможности использовать и испытывать свои неверные теории, мы можем надеяться чему-то научиться, убедившись в их ложности.
Этим объясняется, почему Галилей, несмотря на знакомство с работами Кеплера, продолжал придерживаться гипотезы кругового движения планет. В этом он был совершенно прав ввиду того, что круговое движение можно было объяснить его основными законами сохранения. Часто говорят, что он пытался прикрыть трудности коперниковских циклов и что он неоправданно упрощал теорию Коперника, а также, что ему следовало принять законы Кеплера. Все это говорит, однако, о недостатке исторического понимания — об ошибочном анализе проблемной ситуации третьего мира. Галилей был совершенно прав, работая со смелыми упрощениями, а эллипсы Кеплера тоже были упрощениями, не менее смелыми, чем круги Галилея. Кеплеру тем не менее повезло — его упрощения вскоре использовал и тем самым объяснил Ньютон для проверки своего решения проблемы двух тел.
Почему же Галилей отверг уже известную идею влияния Луны на приливы? Этот вопрос открывает перед нами очень важный аспект данной проблемной ситуации. Во-первых, Галилей отверг влияние Луны потому, что был противником астрологии, которая по существу отождествляла планеты с богами. В этом смысле он был предтечей Просвещения, а также противником астрологии Кеплера, хотя и восхищался Кеплером20). Во-вторых, он работал с механическим принципом сохранения для вращательного движения, а это как будто исключало взаимодействие между планетами. Если бы не попытка Галилея дать объяснение приливов на этом узком основании, мы, возможно, не так скоро узнали бы о том, что это основание слишком узко и что нужны еще какие-то идеи, в частности идея Ньютона о притяжении (а с нею и понятие силы), то есть идеи, которые носили почти астрологический характер и которые казались оккультными самым просвещенным людям того времени, таким как Беркли 21\ Они казались оккультными даже самому Ньютону.
Таким образом, анализ проблемной ситуации Галилея привел нас к оправданию разумности метода Галилея в нескольких аспектах, по которым его критиковали многие историки и в результате мы пришли к лучшему историческому пониманию Галилея. В такой ситуации становятся излишними психологические объяснения, попытки которых предпринимались историками и которые использовали такие понятия, как «честолюбие», «ревность», «агрессивность» или «желание вызвать сенсацию». На их место приходит анализ ситуации с точки зрения третьего мира. Подобным же образом становится излишним критиковать Галилея за «догматизм» из-за того, что он придерживался кругового движения, или вводить понятие загадочной психологической привлекательности
20) См. Popper К. R. Conjectures and Refutations. P. 188.
21) См. Popper К. R. Conjectures and Refutations. P. 188 и глава 6.
«загадочного кругового движения». (Дильтей называет эту идею архети-пической или психологически привлекательной22).) Ведь Галилей следовал верному методу, когда пытался продвинуться как можно дальше при помощи рационального закона сохранения для вращательного движения. (Динамических теорий тогда еще не существовало.)
Этот вывод должен проиллюстрировать, как вместе с нашим пониманием объективной проблемной ситуации Галилея выросло наше историческое понимание роли Галилея. Теперь мы можем обозначить эту проблемную ситуацию «JV\ поскольку она играет роль, аналогичную роли той Pi, которая была у нас раньше. Пробную теорию Питилея мы можем обозначить «ТТ», а попытки критического обсуждения этой теории и устранения ошибок им самим и другими мы можем обозначить «ЕЕ». Хотя Галилей рассчитывал на истинность своей теории, он был далеко не удовлетворен результатами ее критического рассмотрения. Можно сказать, что его Pi была очень близка к его Р\, то есть проблема все еще была открыта.
Гораздо позднее это привело к революционным изменениям (благодаря Ньютону) в проблемной ситуации {Рг)\ Ньютон расширил Галилеев каркас — образованный законами сохранения, — в рамках которого возникла проблема Галилея. Частично ньютоновские революционные изменения состояли в том, что он вернул в теорию Луну, изгнание которой из теории приливов стало естественным следствием галилеевского каркаса (и фона).
Чтобы вкратце подвести итог, скажем, что физический каркас Галилея представлял собой несколько упрощенный вариант коперниковской модели Солнечной системы. Это была система циклов (а может быть, и эпициклов) с постоянной скоростью вращения. Даже Эйнштейн неодобрительно высказывался по поводу галилеевской «приверженности идее кругового движения», которую он считал «ответственной за то, что он не вполне понял закон инерции и его фундаментальное значение» 23\
22) Дильтей говорит о «загадочном круговом движении» ('die geheimnisvolle... Kreisbewegung1 (Dilthey W. Gesammelte Schriften. Band 1. SS. 95-96)) античной астрономии. По-моему, здесь перед нами случай недопонимания, говорящий не в пользу степеней уверенности Дильтея, обсуждавшихся в одной из предыдущих сносок. (Возможно, Дильтей мог бы ответить, что в этой области наука начинается с Ньютона, а он говорит о до-научных идеях. Я думаю, что нельзя принять такой ответ и отрицать, что Галилей был ученым: наука начинается с Анаксимандра или даже еще раньше.)
Краткое, но глубокое исследование проблемы «Птолемей против Коперника» можно найти в работе Neugebauer О. The Exact Sciences in Antiquity. 1957. P. 191 и далее. (Из-за недостаточно четкого различения геометрических и физических проблем даже Нейгебауэр на странице 204 осуждает приверженность Коперника и Галилея к использованию кругов как догматическую.)
23) Приведенная цитата взята со c.xi замечательного предисловия Эйнштейна к работе Галилея: Galilei G. Dialogue Concerning the Two Chief World Systems, перевод Stillman Drake, пересмотренное издание, 1962. Эйнштейн признает, что у Галилея был закон инерции, и нет сомнений в том, что Галилей не вполне (курсив Эйнштейна) понимал его фундаментальное значение. Здесь можно упомянуть о том, что Галилея много критиковали за представление системы Коперника в чересчур упрощенной форме: и действительно, он
Однако он забыл, что, как теория Ньютона основывалась на законе инерции или законе сохранения момента, так и теория циклов — эпициклов в своей наиболее простой форме, ограничивавшейся постоянными скоростями, —• эту форму и предпочитал Галилей, — первоначально основывалась на законе сохранения углового момента. Оба закона сохранения, несомненно, были выбраны «инстинктивно»; может быть, тут имело место нечто подобное отбору предположений под давлением практического опыта: для закона об угловом моменте решающим мог оказаться опыт знакомства с движением хорошо смазанных колес у повозок. Следует также помнить, что античную теорию кругового вращения небес (выведенную из этого опыта) в конце концов сменила теория сохранения углового момента Земли — это указывает на то, что циклы не были ни такими наивными, ни такими загадочными, какими их до сих пор часто считают. В рамках этого каркаса — в противоположность каркасу астрологов — не могло быть никакого взаимодействия между небесными телами. Так что Галилей должен был отвергнуть лунную теорию приливов, которой придерживались астрологи24).
Можем ли мы научиться чему-то новому на этом примере? Я думаю, что можем.
Во-первых, этот пример показывает огромное значение воссоздания проблемной ситуации Галилея (Р\) для понимания теории Галилея (ТГ). Это воссоздание имеет еще большее значение для понимания неудачных теорий, таких как галилеевская, чем для понимания успешных, потому что ее недостатки (недостатки ТГ) могут объясняться недостатками каркаса или фона Pi.
Во-вторых, в данном случае становится очевидным, что воссоздание проблемной ситуации Галилея (Pi), в свою очередь носит характер
критически замечает, что «Птолемей вводит многочисленные эпициклы» (op. cit., с. 341 и далее), но не говорит о том, что Коперник тоже использовал эпициклы. Здесь перед нами проблема исторической интерпретации. Я утверждаю, что Галилей сознательно оставил открытой проблему, возникшую из того, что чересчур упрощенная система Коперника, основанная исключительно на круговом движении с постоянной скоростью, без эпициклов, не совсем точно соответствовала данным наблюдений. На него произвело большое впечатление, что теория соответствовала наблюдениям сравнительно хорошо, и он считал, что чисто геометрические проблемы, оставшиеся открытыми, можно решить только вместе с физическими проблемами. (Он намекал, что, возможно, решение могли бы дать не столь «многочисленные» эпициклы, вихри, или магнетические силы; ср. op. cit., с. 398 и далее). Эта мысль оказалась верной, и не следует забывать о том, что и геометрическое решение Кеплера было все-таки приближением, то есть упрощением.
24) Связь между галилеевской теорией приливов и его отрицанием астрологии обсуждается и истолковывается в моей книге Popper К, R, Conjectures and Refutations, примечание 4 к главе 1 (р. 38) и примечание 4 к главе 8 (с. 188). Я выдвинул типично предположительную интерпретацию (в смысле моей книги Popper К. R. Open Society and its Enemies, 1945. Vol. 1. Ch. 10. P. 171 (русский перевод: Поппер К. Открытое общество и его враги. Под общей редакцией Садовского В. И. М., 1992. Т. I. Гл. 10. С. 215). и в качестве таковой она могла «пролить свет на исторический материал»: она, в частности, помогла мне лучше понять последний абзац галилеевского «Диалога» (op. cit., с. 462; об отношении Галилея к астрологии см. также с. 109 и далее), в котором Галилей упоминает о Кеплере, упрекая его за его астрологические «ребячества».
предположения (а также упрощения или идеализации): это очевидно, учитывая, что мой анализ этой проблемной ситуации (Pi), при всей своей краткости, существенно расходится с мнением других исследователей, пытавшихся понять эту неудачную теорию Галилея. Вместе с тем если моя реконструкция Р\ является предположением, то какую проблему это предположение пытается разрешить? Очевидно, Ри — проблему понимания теории Галилея.
В-третьих, я утверждаю следующее: наша проблема понимания Ри находится на более высоком уровне, чем Р\. Иначе говоря, проблема понимания — это метапроблема; она касается и ТТ, и Pi. В соответствии с этим, теория, разработанная для решения проблемы понимания, — это метатеория, поскольку в задачи этой теории входит выяснение в каждом конкретном случае, из чего на самом деле состоят Pi, ТТ, ЕЕ и Рг.
Кстати, это не следует понимать так, что метатеория должна в каждом конкретном случае только исследовать структуру Pi, ТТ и так далее, некритично принимая саму схему (Pi -+ ТТ -> ЕЕ -+ Р2). Напротив, схема, подчеркнем еще раз, представляет собой упрощение, поэтому она должна при необходимости уточняться или даже коренным образом изменяться.
В-четвертых, я утверждаю, что всякая попытка (кроме самых тривиальных) понять некоторую теорию обязательно ведет к историческому исследованию этой теории и соответствующей проблемы, которые таким образом становятся частью объекта исследования. Если это была научная теория, получится исследование в области истории науки. Если теория была, скажем, исторической, получиться исследование в области истории историографии. Проблемы, которые эти исторические исследования пытаются решить, будут метапроблемами, которые не следует путать с проблемами, являющимися объектом исследования.
В-пятых, я утверждаю, что историю науки следует воспринимать не как историю теорий, а как историю проблемных ситуаций и их изменения (иногда едва заметного, иногда революционного) в ходе попыток решения соответствующих проблем. С точки зрения истории, неудачные попытки могут при этом оказаться не менее важными для дальнейшего развития, чем успешные.
В-шестых, я утверждаю (уточняя пункт три), что следует четко различать метапроблемы и метатеории историка науки (которые находятся на уровне Ри)) и проблемы и теории ученых (которые находятся на уровне Pi). Их очень легко спутать, потому что, если мы сформулируем проблему историка в виде вопроса: «Какова была проблема Галилея?», кажется, что ответ будет: «Pj», но Pi (в отличие от высказывания «Проблема Галилея была Pi») как будто скорее находится на уровне объекта, а не на метауровне 25\ так что между этими двумя уровнями возникает путаница.
25) На самом деле ответом является историческое предположение о проблеме Галилея (Pi). Метапроблемы историка и его предположительные ответы будут далее обсуждаться более подробно.
Вместе с тем, вообще говоря, для этих двух уровней нет общих проблем. Это легко видеть: две пробные теории об одном и том же объекте часто сильно отличаются друг от друга. Два историка науки, соглашаясь по поводу «фактов», могут понимать или интерпретировать их очень по-разному (иногда дополняя друг друга, а иногда и противореча друг другу). Они могут даже расходиться в мнениях о том, в чем заключаются их проблемы. Поэтому, вообще говоря, у них не будет общих проблем ни друг с другом, ни тем более с теорией, являющейся объектом их исследования и интерпретации.
Кроме того, для интерпретации той или иной теории метатеоретик волен использовать все, что может ему пригодиться — например, он может сопоставлять эту теорию с какими-нибудь другими, радикально отличными от нее конкурирующими теориями. Таким образом, некоторые структурные единицы третьего мира, составляющие метатеорию, могут быть совершенно непохожи на единицы, составляющие теорию, подлежащую интерпретации или пониманию.
Это важный момент. Он устанавливает a fortiori*, что даже если бы мы могли говорить хоть сколько-нибудь осмысленно (что я склонен отрицать) о такой вещи, как сходство между мысленными содержаниями объектов третьего мира, с одной стороны, и теми мыслительными процессами второго мира, посредством которых мы усваиваем эти содержания, с другой стороны, я и тогда все-таки отрицал бы существование — в общем случае, на любом проблемном уровне — какого бы то ни было сходства между содержанием и соответствующим мыслительным процессом. Действительно, принадлежащий третьему миру метод исторического понимания, который я пытаюсь описать, — это метод, который везде, где только возможно, заменяет психологические объяснения на анализ отношений третьего мира: вместо психологических объяснительных принципов мы используем относящиеся к третьему миру соображения в основном логического характера, и я утверждаю, что из такого анализа может вырасти наше историческое понимание.
Седьмой и, возможно, самый важный пункт касается того, что я иногда называл ситуационной логикой, или ситуационным анализом26^ '. (Последнее название, возможно, предпочтительнее, потому что может показаться, что первое название подразумевает некую детерминистскую теорию человеческой деятельности, а я, конечно, далек от мысли предлагать что-либо подобное.)
Под ситуационным анализом я подразумеваю определенный вид пробных или предположительных объяснений некоторого человеческого
* A fortiori (лат.) — тем более. — Прим. пер.
26^Я описал метод ситуационной логики, или ситуационного анализа, в своей книге Popper К. R. The Open Society and its Enemies, vol. II, ch. 14, особенно р. 97 (русский перевод: Поппер K.P. Открытое общество и его враги. М., 1992, т. 2, гл. 14, особенно с. 115-116) и в моей книге Popper К. R. The Poverty of Historicism», 1957, разделы 31 («Ситуационная логика в истории», см. в особенности р. 149) и 32 («Институциональная теория прогресса») (русский перевод: Поппер К. Р. Нищета историцизма. М, 1993; странице 149 оригинала соответствует с. 171-172 русского издания).
действия, апеллирующих к той ситуации, в которой находится человек, производящий действие. Это может быть историческое объяснение, например, когда нам захочется объяснить, как и почему была создана определенная структура идей. Конечно, творческое действие никогда нельзя полностью объяснить. И все же мы можем попытаться в виде предположения построить идеализированную реконструкцию проблемной ситуации, в которой находился субъект действия, и в той мере, в какой нам это удастся, его действие станет «понимаемым» (или «доступным рациональному пониманию»), то есть адекватным его ситуации, какой он ее видел. Этот метод ситуационного анализа можно назвать приложением принципа рациональности.
Одой из задач ситуационного анализа является различение ситуации, какой ее видел субъект, и ситуации, какой она была на самом деле (и то, и другое, разумеется, предположительно)27). Таким образом, при помощи ситуационного анализа историк науки не только пытается объяснить теорию, предложенную ученым в качестве адекватной, но может попытаться объяснить и неудачу ученого при построении такой теории.
Иными словами, наша схема решения проблем посредством предположений и опровержений или какая-то подобная ей схема могут использоваться в качестве объяснительной теории человеческих действий, поскольку действие мы можем интерпретировать как попытку решения некоторой проблемы. Теория, объясняющая соответствующее действие, будет в основном состоять из предположительной реконструкции проблемы и ее фона. Теория такого рода вполне может быть хорошо проверяемой.
Я попытался ответить на вопрос: «Как мы можем понять научную теорию или улучшить свое понимание этой теории?» И я предположил, что мой ответ — в терминах проблем и проблемных ситуаций — применим далеко за пределами научных теорий. Мы можем — по крайней мере в некоторых случаях — применять его даже к произведениям искусства: мы можем предположить, в чем состоит проблема художника, и мы можем
' Во многих случаях мы можем воссоздать объективно (хотя и предположительно) (а) ситуацию, какой она была, и (Ь) совершенно иную ситуацию, какой она представлялась субъекту, или как субъект ее понимал, или интерпретировал. Интересно, что это можно сделать даже в истории науки. Примером может служить волновая механика Шредингера. Шредингер не интерпретировал свою проблему как статистическую (то, что это статистическая проблема, выяснилось только после знаменитой «статистической интерпретации» Бора — см. мою работу «Квантовая механика без „наблюдателя»«(Popper К. Я. 'Quantum Mechanics Without «The Observer'«// Quantum Theory and Reality. Ed. by Bunge Mario. Berlin, Heidelberg, New York: Springer-Verlag, 1967. P. 7-44). Есть много других сходных примеров — и старых, и новых. Кеплер понимал свою проблему как открытие пифагорейской мировой гармонии. Эйнштейн формулировал проблему общей относительности с помощью требования ковариантности, и хотя он принимал критику Е. Кречмана [Kretschmann E. // Ann. Physik, Bd. 35, S.575, 1917), который назвал это требование пустым, все же Эйнштейн явно был убежден, что его можно переформулировать так, чтобы оно могло выполнять предназначенную ему роль, хотя удовлетворительной переформулировки он так и не дал. Аналогичный пример из философии (связанный с проблемой Канта: «Как возможно чистое естествознание (pure natural science)?») разбирается в моей книге Popper К. R. Conjectures and Refutations, глава 2, раздел X, особенно pp. 94-96.
подкрепить это предположение независимыми фактическими данными, и этот анализ может помочь нам понять его работу 28\
(В каком-то смысле промежуточную позицию между интерпретацией научной теории и интерпретацией произведения искусства, возможно, занимает задача реставрации поврежденного произведения искусства — скажем, восстановление поэмы, найденной в виде записи на поврежденном папирусе).