
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Cost-minimization
|
|
A profit-maximizing firm must minimize it's level of costs. To investigate this process of cost-minimization, we must combine an isoquant curve with a family of isocost curves (as in the diagram below).
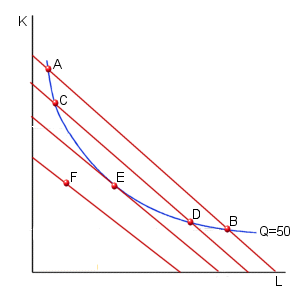
The problem facing the firm is to minimize the costs of producing a given level of output (Q= 50 in this example). To produce 50 units of output, the firm must remain on the Q=50 isoquant. Cost-minimization requires that it select the combination of inputs that results in the lowest level of total costs. Consider point A in the diagram above. While the firm is producing 50 units of output at this point, any other point on the isoquant between points A and B would allow the production of this level of output at a lower level of total costs. Suppose the firm shifts to the combination of inputs given by point C in the diagram. Production at this point is less expensive than at point A (since it corresponds to a lower isoquant), but this still isn't the lowest possible cost. Any point on the isoquant between points C and D would allow for lower cost production. In general, we can observe that when an isocost curve crosses an isoquant at two points, there will always be some points between these two points at which costs would be lower.
Consider, however, the situation at point E. No other combination of inputs can result in lower costs while still allowing the production of 50 units of output. Points such as point f would have lower costs, but would not allow the production of 50 units of output (since point F lies below the isoquant).
Thus, we can note that a firm minimizes its total cost of producing any given level of output when it operates at a point of tangency between its isoquant and an isocost curve. At this point of tangency, the slopes of the isoquant and the isocost curve must be equal. Thus:
-MRTS = -w/c
or, simplifying:
MRTS = w/c
This cost-minimization condition, more intuitively, requires that the firm use a mix of inputs at which the firm's value of labor in terms of capital (the MRTS) equals the relative cost of labor in terms of capital (w/c).
An alternative way of expressing this condition is to make use of the fact that the MRTS will always equal the ratio of the MP of labor to the MP of capital:
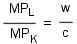
Using a little algebraic manipulation, we have the cost-minimization rule given by:
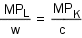
This cost-minimization rule (one that you probably learned in your micro principles course --without the more formal derivation) requires that the marginal product per dollar spent on any one input must equal the marginal product per dollar spent on any other input.