
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Використання графічної бібліотеки opengl 3 страница
|
|
де параметр mode визначає, з яким набором матриць виконуватимуться наступні операції. Значення параметра вказуються у таблиці 12.5.
Таблиця 12.5 – Типові параметри функції glMatrixMode()
| Значення параметра | Коментар |
| GL_MODELVIEW | Послідовність операцій над матрицями застосовується до матриці вигляду |
| GL_PROJECTION | Послідовність операцій над матрицями застосовується до матриці проекції |
| GL_TEXTURE | Послідовність операцій над матрицями застосовується до матриці текстури |
Визначення елементів матриці забезпечує функція glLoadMatrix*():
void glLoadMatrix [f d] (GLtype *m);
у якій параметр m – визначає покажчик на 4x4-матрицю. Матриця зберігається як 16 дійсних значень і має тип float або double:
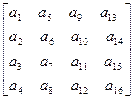
Команда замінює поточну матрицю на матрицю, визначену параметром m. Поточною є одна з матриць – видова, проекцій або текстури, в залежності від обраного функцією glMatrixMode().
Наступна функція glLoadIdentify() також замінює поточну матрицю на одиничну (матрицю ідентичності).
void glLoadIdentify ();
За змістом вона є еквівалентом glLoadMatrix*() із тією різницею, що матриця має головну діагональ, складену з одиниць, а усі інші елементи мають значення 0:

Ще одна функція – glMultMatrix*() здійснює операцію перемножування матриці m (розміром 4x4) на поточну матрицю:
void glMultMatrix [f d] (GLtype *m);
Результатом glMultMatrix*() є встановлення поточної матриці M · T. Зазначимо, що з точки зору обчислень ця операція може бути досить складною.
12.5.4 Перетворення виду
Перетвореннями виду змінюють позицію і орієнтацію точки спостереження за об’єктом. Якщо згадати аналогію камери, можна сказати, що перетворення вигляду (вибір кадру) розміщує штатив камери, орієнтуючи саму камеру на об’єкт. Перетворення виду складаються з паралельних перенесень та поворотів. Для досягнення певної композиції сцени можна або перемістити камеру, або пересунути усі об’єкти у протилежному напрямі. Наприклад, перетворення моделі, що включає обертання об’єкта проти годинникової стрілки є еквівалентним перетворенню виду, що обертає камеру у протилежному напрямі.
Обертання об’єктів здійснюється за допомогою команди glRotate*():
void glRotate [f d] (GLtype angle, GLtype x, GLtype y, GLtype z);
де обертання на кут angle здійснюється навколо вектора, спрямованого з центру системи координат у точку (x, y, z). Виконання команди повертає усі об’єкти.
Припустимо, що у OpenGL-програмі визначаються осі координат, після чого у залежності від значення кута відбувається обертання прямокутника навколо осі X (рисунок 12.4). Такі дії програми відображаються такою частиною коду:
glLineWidth(2.0);
glBegin(GL_LINES); // визначення осей координат
glColor3f(1.0, 0.0, 0.0);
glVertex3f(25.0f, 0.0f, 0.0f); glVertex3f(0.0f, 0.0f, 0.0f); // вісь X
glColor3f(0.0, 1.0, 0.0);
glVertex3f(0.0f, 25.0f, 0.0f); glVertex3f(0.0f, 0.0f, 0.0f); // вісь Y
glColor3f(0.0, 0.0, 1.0);
glVertex3f(0.0f, 0.0f, 25.0f); glVertex3f(0.0f, 0.0f, 0.0f); // вісь Z
glEnd();
glColor3f(0.0, 0.0, 1.0);
glRotatef(30*i, 1, 0, 0); // обертання навколо X з кроком кута 30 градусів
glRectf(3.0, 3.0, 6.0, 6.0); // відображення прямокутника

а) б)
Рисунок 12.4 – Використання команди glRotate*() (кути а – 00, б – 600)
Перенесення об’єктів здійснюється за допомогою команди glTranslate*():
void glTranslate [f d] (GLtype x, GLtype y, GLtype z);
За допомогою цієї команди здійснюється перенесення об’єкта на відстань x вздовж осі X, y – вздовж осі Y, z – вздовж осі Z.
Якщо у OpenGL-програмі у залежності від зміни координати x відбувається перенесення об’єкта, дії програми можна відобразити такою частиною програмного коду:
glLineWidth(2.0)
glBegin(GL_LINES);
glColor3f(1.0, 0.0, 0.0);
glVertex3f(25.0f, 0.0f, 0.0f); glVertex3f(0.0f, 0.0f, 0.0f);
glColor3f(0.0, 1.0, 0.0);
glVertex3f(0.0f, 25.0f, 0.0f); glVertex3f(0.0f, 0.0f, 0.0f);
glColor3f(0.0, 0.0, 1.0);
glVertex3f(0.0f, 0.0f, 25.0f); glVertex3f(0.0f, 0.0f, 0.0f);
glEnd();
glColor3f(0.0, 0.0, 1.0);
glTranslatef(-10+i, 0, 0); // перенесення вздовж осі X
glRectf(3.0, 3.0, 6.0, 6.0);
Результат виконання такого програмного коду зображено на рисунку 12.5.
Рисунок 12.5а відповідає виклику з i=0 (тобто glTranslatef(-10, 0, 0);), рисунок 12.5б – виклику з i=10 (glTranslatef(0, 0, 0);).

а) б)
Рисунок 12.5 – Використання команди glTranslate*()
Масштабування розмірів об’єктів вздовж визначених координатних осей здійснюється функцією glScale*():
void glScale [f d] (GLtype x, GLtype y, GLtype z);
Під час виконання перерахованих команд перетворення об’єктів OpenGL здійснює перемноження поточної матриці (M) на відповідну матрицю обертання (R) або перенесення (T) чи масштабування (S) і розміщує результат (M · R, M · T або M · S) замість поточної матриці.
Якщо у програми, описаної для обертання та трансляції, додати рядок:
glScalef(0.5*i, 0.5*i, 1.0);
можна отримати вікна програм, зображені на рисунку 12.6.
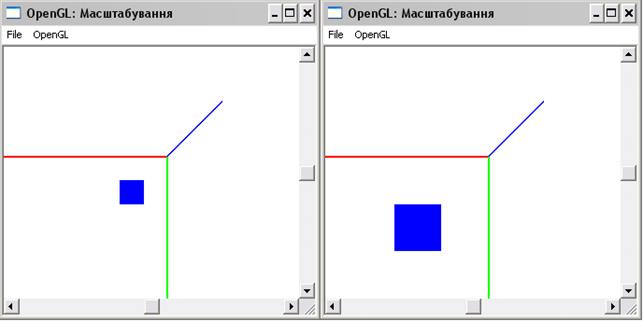
а) б)
Рисунок 12.5 – Використання команди glScale*() (а – масштаб 0.5, б – 1.0)
Доволі часто доводиться створювати сцену на початку системи координат або іншому зручному місці, а потім переглядати її з певної точки. Команда gluLookAt() призначена саме для цього:
void gluLookAt (GLdouble eyex, GLdouble eyey, GLdouble eyez
GLdouble centerx, GLdouble centery, GLdouble centerz,
GLdouble upx, GLdouble upy, GLdouble upz);
Така команда приймає три набори аргументів: точку спостереження (eyex, eyey, eyez); контрольну точку (centerx, centery, centerz), до якої спрямовується камера; точку, що характеризує вектор верхнього напряму (upx, upy, upz) – напрям знизу-вгору зони видимості. Для роботи слід обрати точку спостереження, з якої отримується необхідний вид. Контрольна точка зазвичай знаходиться приблизно посередині сцени. Встановлення напряму вгору (Up-vector) інколи може викликати певні складнощі і залежатиме від положення самого об’єкта.
12.5.5 Керування матричними стеками
Матриці видового перетворення та проекцій, що створювалися раніше, насправді були лише верхніми елементами у матричних стеках, що використовуються OpenGL. Матричні стеки є дуже корисним способом побудови ієрар-хічних комп’ютерних моделей. У тих випадках, коли необхідно відображати декілька разів одні й ті самі об’єкти, можна застосувати переходи від одного елемента матричного стека, що характеризує певний стан геометричного перетворення координат, до іншого елемента стека.
Оскільки перетворення координат зберігаються у вигляді матриць, матричний стек є ідеальним механізмом виконання успішних операцій запам’ятовування, паралельного перенесення та відміни. Усі матричні операції, описані до сих пір (glLoadMatrix(), glMultMatrix(), glLoadIdentify()), взаємодіють з поточною матрицею, тобто з верхньою матрицею стека. Операції з матричним стеком забезпечуються командами glPushMatrix() та glPopMatrix():
void glPushMatrix(void);
void glPopMatrix(void);
Команда glPushMatrix() додає поточну матрицю у вершину стека. При цьому зберігаються усі попередні координатні матриці – як характеристики попередніх станів системи.
Команда glPopMatrix() видаляє верхівку стека – координатну матрицю із характеристикою певного стану.
Обидві команди доречно використовувати під час побудови складених об’єктів OpenGL-програм.
Використовуючи команду glPushMatrix() можна запам’ятати поточний стан координатних матриць графічної системи, зробити необхідні виклики команд OpenGL для побудови графічних об’єктів, потім здійснити видові перетворення (наприклад перенесення, обертання чи масштабування) і знову-таки побудувати необхідні примітиви OpenGL. Для повернення у попередній (до видових перетворень) стан систем координат OpenGL у програмі буде достатньо використати команду glPopMatrix().
Розглянемо приклади побудови деяких складених об’єктів:
1. Припустимо, що нам необхідно побудувати графічний об’єкт типу ракета, що складатиметься з циліндра – корпуса ракети, конуса – носу ракети та радіально розташованих чотирьох трикутників – стабілізаторів. Для цього видозмінимо текст функції OnOpenGLFirst() у спосіб, наведений у прикладі 12.3. Результат роботи програми зображено на рисунку 12.6. Послідовність побудови пояснюється у коментарях.
Приклад 12.3 – Побудова складеного об’єкта із матричними перетвореннями (ракета)
void CMain:: OnOpenGLFirst()
{ glRotatef(360.0*hspos/100, 0, 1, 0); // обертання навколо осі Y (горизонтальна смуга прокрутки)
glRotatef(360.0*vspos/100, 1, 0, 0); // обертання навколо осі X (вертикальна смуга прокрутки)
glLineWidth(2.0);
glPushMatrix(); // запам'ятаймо положення основи циліндра
glTranslatef(0.0, -1.0, 0.0);
auxWireCylinder(1.5, 11.0); // будуємо циліндр: перший параметр - радіус, другий - довжина
glTranslatef(0.0, -10.0, 0.0); // перемістимося до верхівки циліндра
glRotatef(90.0, 1.0, 0.0, 0.0); // повертаємо конус на 90 градусів навколо осі Y
auxWireCone(1.5, 3.0); // будуємо конус: перший параметр - радіус, другий - висота
glPopMatrix(); // повертаємося до основи ракети
GLuint stab; // оголошення списку «стабілізатор»
stab=glGenLists(1); // генерація списку
glNewList(stab, GL_COMPILE); // список побудови стабілізатора
glBegin(GL_TRIANGLES);
glVertex3f(1.5f, 0.0f, 0.0f); glVertex3f(3.5f, 0.0f, 0.0f); glVertex3f(1.5f, -3.0f, 0.0f);
glEnd();
glEndList();
// перший стабілізатор - в основній системі координат
glCallList(stab); // виклик списку - побудова стабілізатора
// другий стабілізатор - повернемо на 90 градусів навколо осі Y
glPushMatrix(); // запам'ятаймо поточну систему координат
glRotatef(90.0, 0.0, 1.0, 0.0); // здійснюємо обертання на 90 градусів
glCallList(stab); // виклик списку - побудова стабілізатора
glPopMatrix(); // повернення до основної системи координат
// третій стабілізатор - повертається на 180 градусів
glPushMatrix();
glRotatef(180.0, 0.0, 1.0, 0.0);
glCallList(stab);
glPopMatrix();
// четвертий стабілізатор - повертається на 270 градусів
glPushMatrix();
glRotatef(270.0, 0.0, 1.0, 0.0);
glCallList(stab);
glPopMatrix();
}

Рисунок 12.6 – Приклад побудови складеного об’єкта із матричними перетвореннями
2. У другому прикладі побудуємо модель промислового робота. Робот будувати дещо складніше. Кожен робот складається з декількох рухомих ланок. З метою скорочення програмного коду рухомість буде відключено, хоча керування окремими ланками робота реалізувати досить нескладно. Для цього текст функції OnOpenGLFirst() запишемо у спосіб, наведений у прикладі 12.4. Робота програми наведена на рисунку 12.7, а послідовність побудови пояснюється у коментарях.
Для обох випадків побудови слід вказати на певні особливості.
Каркасні циліндри будуються командою auxWireCylinder() негативно орієнтованими вздовж осі Y, а свій початок мають у точці (0.0, 1.0, 0.0), хоча природнім початком, з точки зору користувача, має бути центр системи коорди- нат – точка (0.0, 0.0, 0.0). Тому для коректної роботи програми необхідно зміщувати циліндри за допомогою команди glTranslatef(0.0, -1.0, 0.0).
Конуси також мають свої особливості. Конус за замовчуванням будується орієнтованим вершиною вздовж осі Z у її позитивному напрямку. Центр фігури розташовується на початку координат (0.0, 0.0, 0.0), а її основа – у площині XY.
Команда побудови призм auxWireBox() діє повністю, передбачено і будує об’єкти з центром на початку координат. Зокрема виклик команди auxWireBox(2, 2, 2) забезпечує побудову куба із стороною 2 і центром на початку системи координат.
Приклад 12.4 – Побудова каркасного зображення робота
void CMain:: OnOpenGLThird()
{ glPushMatrix();
glTranslatef(0.0, -3.0, 0.0); // початкове переміщення сцени
glRotatef(360.0*vspos/100, 0, 1, 0); // 3D-обертання навколо осі Y
glRotatef(180, 0, 0, 1); // початковий поворот сцени на 180 градусів навколо осі Z
glLineWidth(2.0);
glPushMatrix(); // запам'ятаймо положення основи робота
glRotatef(90.0, 1.0, 0.0, 0.0); // повертаємо конус на 90 градусів навколо осі X
glColor3f(0.0, 0.0, 1.0);
auxWireCone(1.5, 1.0); // перший параметр - радіус, другий - довжина
glPopMatrix(); // повертаємося до основи робота
glTranslatef(0.0, -1.0, 0.0); // змінимо висоту на -1.0 вздовж осі Y
glColor3f(0.0, 0.5, 0.5);
auxWireCylinder(0.6, 4.0); // будуємо циліндр - колону робота
glPushMatrix(); // запам'ятаймо положення кінця циліндра
// Циліндр кріплення плеча розвертається на 90 градусів навколо осі X
glTranslatef(0.0, -3.0, 0.0); // переміщення у кінець колони
glRotatef(90.0, 1.0, 0.0, 0.0); // повертаємося на 90 градусів навколо осі X
glColor3f(1.0, 0.0, 0.0);
auxWireCylinder(0.6, 2.0); // циліндр кріплення плеча
// Призма формування плеча
glRotatef(180.0*hspos/100, 0.0, 1.0, 0.0); // рух плеча горизонтальною прокруткою
glTranslatef(1.0, 0.5, 0.0); // переміщення у кінець кріплення
glColor3f(0.5, 0.5, 0.5);
auxWireBox(2.0, 1.0, 1.2); // призма плеча
// Кінцевий циліндр формування плеча
glTranslatef(1.0, -0.5, 0.0); // переміщення у кінець призми
glColor3f(1.0, 0.0, 0.0);
auxWireCylinder(0.6, 1.0); // кінцевий циліндр формування плеча
// Призма формування ліктя
glRotatef(90.0*hspos/100, 0.0, 1.0, 0.0); // рух ліктя горизонтальною прокруткою
glTranslatef(1.0, 0.5, 0.0); // переміщення у кінець кріплення
glColor3f(0.0, 0.5, 0.5);
auxWireBox(2.0, 1.0, 0.8); // призма плеча
// Кінцевий циліндр формування ліктя
glTranslatef(1.0, -0.5, 0.0); // переміщення у кінець ліктя
glColor3f(1.0, 0.0, 0.0);
auxWireCylinder(0.4, 1.0); // кінцевий циліндр формування ліктя
// Схват робота
glColor3f(1.0, 0.0, 0.0);
glTranslatef(0.5, 0.5, 0.0); // переміщення у центр кінця плеча
auxWireBox(1.0, 0.7, 0.4); // призма основи cхвату
glColor3f(0.0, 0.0, 1.0);
glRotatef(90.0, 0.0, 0.0, 1.0); // повертаємося 90 градусів навколо осі Z
glTranslatef(0.2, -1.5, 0.0); // переміщення у край призми схвату
auxWireCylinder(0.1, 0.4); // перший циліндр пальця
glTranslatef(-0.4, 0.0, 0.0); // переміщення у другий край призми схвату
auxWireCylinder(0.1, 0.4); // другий циліндр пальця
glPopMatrix(); // повертаємося до кінця колони
glPopMatrix();
}

Рисунок 12.6 – Результати роботи програми із побудовою
каркасного зображення робота
12.5.6 Очищення вікна
Якщо згадувати виведення зображень у контекст пристрою вікна, очищення здійснюється простим зарисовуванням фоновим кольором необхідної частини вікна. З точки зору вирішення тривимірних завдань OpenGL ця проблема не є надто простою, бо доводиться встановлювати систему координат, положення точки спостереження, напрямок спостереження. Тому найбільш ефективним засобом є використання спеціальних команд.
Кольори пікселів, що обробляються апаратними засобами комп’ютерної графіки, відомі під назвою бітових площин. Вже згадувалося, що існує два методи зберігання такої інформації. Один метод передбачає збереження чотирьох компонентів кольору пікселів – червоного, зеленого, синього та альфа (режим RGBA) – безпосередньо у бітових площинах, другий забезпечує зберігання єдиного значення індексу, що посилається на таблицю відповідності кольорів. Частіше використовується режим RGBA.
Команда glClearColor() встановлює поточний колір очищення буфера кольору:
void glClearColor(GLclampf red, GLclampf green, GLclampf blue, GLclampf alpha);
Для роботи з функцією необхідно вказати колір очищення у форматі RGBA.
Безпосереднє очищення буфера кольору здійснюється командою glClear():
void glClear(GLbitfield mask);
де параметром mask вказується необхідний для очищення буфер (або комбінація буферів – за допомогою символу |). Буферами можуть бути: буфер кольору GL_COLOR_BUFFER_BIT, глибини GL_DEPTH_BUFFER_BIT, буфер-накопичувач GL_ACCUM_BUFFER_BIT та трафарету GL_STENCIL_BUFFER_BIT. Як правило колір очищення задається на початку програми, потім буфери очищуються за необхідністю. Операції очищення є нескладними за записом. Для очищення буферів кольору та глибини можна використати таку послідовність команд:
glClearColor(0.0, 0.0, 0.0);
glClearDepth(1.0);
glClear(GL_COLOR_BUFFER_BIT, GL_DEPTH_BUFFER_BIT);
12.6 Засоби накладення текстур
12.6.1 Загальна інформація
У розглянутих раніше програмах геометричні примітиви відображувалися або незаповненими, або заповнювалися кольором, встановленим для ліній, що складали примітив. Однак, якщо мати на меті відображення, наприклад, цегляного муру без накладення текстур, доведеться відображати кожну цеглину окремим багатокутником. Без застосування текстур великий плоский мур, що насправді є великим багатокутником, потребує побудови тисяч окремих цеглин. Але навіть і тоді цегла здаватиметься надто штучною і регулярною, не виглядатиме реалістично.
Накладення текстур дозволяє вклеїти зображення цегляного муру (яке можливо отримано з фотографії справжнього муру) у багатокутник і зобразити цілий мур простим багатокутником. Використання текстур надає і додаткові можливості. Якщо розглядати мур у перспективі, цеглини мають здалеку здаватися меншими, ніж з близької відстані. Текстури можна використати для зображення рослинності на поверхні землі або рельєфу місцевості під час моделювання польоту літака, для надання елементам оформлення програми реалістичних властивостей, подібних мармуру, деревині або тканинам. Хоча, зазвичай, текстури використовуються для заповнення багатокутників, їх можна застосувати до усіх примітивів – точок, прямих ліній, бітових зображень [4].
З програмної точки зору текстури є прямокутними масивами даних: даних про колір, яскравість або альфа-компоненти. Індивідуальні значення текстурного масиву часто називають елементами текстури або текселями (texels). Прямокутна текстура може накладатися на непрямокутні області і це може ускладнювати та уповільнювати процес відображення графічних примітивів.
Про текстури можна казати досить багато [4, 5]. У нашому випадку залишається навести загальний порядок їх застосування та конкретні працездатні приклади.
12.6.2 Створення і використання простих текстур
Для застосування текстур можна визначити формальну послідовність:
1) створити текстурний об’єкт та визначити його текстури;
2) вказати у який спосіб має застосовуватися текстура;
3) дозволити накладення текстур;
4) вивести сцену із одночасним зазначенням текстурних та геометричних координат або у інший спосіб.
Створення текстурних об’єктів доречно у тих випадках, коли у програмі визначається декілька різних типів структур. Процедура створення текстурних об’єктів дозволяє, створивши текстуру лише один раз, багаторазово використати її для накладення на різні графічні об’єкти.
Команда glGenTextures() забезпечує генерацію числового ідентифікатора текстури:
void glGenTextures(GLsizei n, GLuint *textures);
де n – кількість генерованих текстурних об’єктів, textures – покажчик на перший елемент масиву, у якому зберігаються імена текстур.
Команда glBindTexture() під час першого використання створює новий текстурний об’єкт, якому присвоює ім’я, задане аргументом texture:
void glBindTexture(GLenum target, GLuint texture);
а параметр target визначає тип текстури GL_TEXTURE_1D – одновимірна, GL_TEXTURE_2D – двовимірна, GL_TEXTURE_3D – тривимірна. Якщо текстурний об’єкт створено раніше, виклик glBindTexture() забезпечує активізацію текстурного об’єкта.
Найчастіше використовуються двовимірні текстури. Для їх визначення використовується OpenGL-команда glTexImage2D():
void glTexImage2D(GLenum target, GLint level, GLint internalformat, GLsizei width, GLsizei height, GLint border, GLenum format, GLenum type, const GLvoid *pixels);Ця команда визначає фізичні параметри текстури: двовимірність, мас-штаб, властивості кольору, розміри зображення, формат кольору, тип піксельних даних. Останнім параметром команди є, власне, масив даних, що представляють опис текстури. Параметри команди та пояснення до них подані у таблиці 12.6.
Таблиця 12.6 – Параметри команди glTexImage2D()
| Ім’я параметра | Коментар |
| target | цільова текстура, має дорівнювати GL_TEXTURE_2D |
| Level | рівень деталізації, 0 – базове значення, n – масштаб зменшення |
| internalformat | кількість компонентів кольору у текстурі; може приймати значення 1, 2, 3, 4 або значення символьних констант: GL_ALPHA, GL_ALPHA4, GL_ALPHA8, GL_ALPHA12, GL_ALPHA16, GL_LUMINANCE, GL_LUMINANCE4, GL_LUMINANCE8, GL_LUMINANCE12, GL_LUMINANCE16, GL_LUMINANCE_ALPHA, GL_LUMINANCE4_ALPHA4, GL_LUMINANCE6_ALPHA2, GL_LUMINANCE8_ALPHA8, GL_LUMINANCE12_ALPHA4, GL_LUMINANCE12_ALPHA12, GL_LUMINANCE16_ALPHA16, GL_INTENSITY, GL_INTENSITY4, GL_INTENSITY8, GL_INTENSITY12, GL_INTENSITY16, GL_R3_G3_B2, GL_RGB, GL_RGB4, GL_RGB5, GL_RGB8, GL_RGB10, GL_RGB12, GL_RGB16, GL_RGBA, GL_RGBA2, GL_RGBA4, GL_RGB5_A1, GL_RGBA8, GL_RGB10_A2, GL_RGBA12, або GL_RGBA16 |
| Продовження табл. 12.6. | |
| width | ширина зображення текстури (має бути числом 2 n + 2(межа) при цілому n) |
| height | висота зображення текстури (має бути числом 2 m + 2(межа) при цілому m) |
| border | ширина рамки (0 або 1) |
| format | формат піксельних даних; приймає 9 символьних значень: GL_RGBA, GL_RGB, GL_RED, GL_BLUE, GL_ALPHA, GL_GREEN, GL_COLOR_INDEX, GL_LUMINANCE, GL_LUMINANCE_ALPHA, |
| type | тип даних піксельних даних, значення GL_UNSIGNED_BYTE, GL_BYTE, GL_BITMAP, GL_UNSIGNED_SHORT, GL_SHORT, GL_UNSIGNED_INT, GL_INT, and GL_FLOAT |
| pixels | покажчик на масив даних із зображенням |
Визначення парамерів текстури може забезпечуватися командами сімей-ства glTexParameter*():
void glTexParameteri(GLenum target, GLenum pname, GLint param); void glTexParameterfv(GLenum target, GLenum pname, const GLfloat *params);
Команда glTexParameter*() визначає параметри способу відображення текстури під час її застосування. Особливо це важливо в умовах неспівпадання розмірів текстури з розмірами об’єктів. При цьому може здійснюватися зменшення елементів текстури до розмірів пікселя (параметр GL_TEXTURE_MIN_FILTER), збільшення (GL_TEXTURE_MAG_FILTER), згортання координати x (GL_TEXTURE_WRAP_S) або y (GL_TEXTURE_WRAP_T).
Параметри команди та пояснення до них подані у таблиці 12.7.
Таблиця 12.7 – Параметри команди glTexParameter *()
| Ім’я параметра | Коментар |
| Target | цільова одно- (GL_TEXTURE_1D) або двовимірна (GL_TEXTURE_2D) текстура |
| Pname | символічне ім’я параметра текстури: GL_TEXTURE_MIN_FILTER, GL_TEXTURE_MAG_FILTER, GL_TEXTURE_WRAP_S, GL_TEXTURE_WRAP_T |
| Param | Значення параметра pname |
| params | Покажчик на масив значень параметра pname, що задає функцію, яка використовується для застосування текстури до пікселя і може приймати такі значення: GL_NEAREST, GL_LINEAR, GL_NEAREST_MIPMAP_NEAREST, GL_LINEAR_MIPMAP_NEAREST, GL_NEAREST_MIPMAP_LINEAR, GL_LINEAR_MIPMAP_LINEAR |
Можливі значення параметрів pname і param зазначені у таблиці 12.8
Таблиця 12.8 – Значення параметрів pname і param команди glTexParameter *()
| Параметр | Коментар та значення |
| GL_TEXTURE_WRAP_S | Параметр згортання s -координати текстури у значення GL_CLAMP або GL_REPEAT |
| GL_TEXTURE_WRAP_T | Параметр згортання t -координати текстури у значення GL_CLAMP або GL_REPEAT |
| GL_TEXTURE_MAG_FILTER | Функція збільшення текстури Значення: GL_NEAREST або GL_LINEAR |
| Продовження табл. 12.8 | |
| GL_TEXTURE_MIN_FILTER | Функція мінімізації текстури. Значення: GL_NEAREST, GL_LINEAR, GL_NEAREST_MIPMAP_NEAREST, GL_NEAREST_ MIPMAP_LINEAR, GL_LINEAR_MIPMAP_NEAREST, GL_LINEAR_ MIPMAP_LINEAR |
| GL_TEXTURE_BORDER_COLOR | Колір рамки. Будь-які чотири значення у діапазоні [0.0, 1.0] |
| GL_TEXTURE_PRIORITY | Рівень пріоритету. Діапазон значень [0.0, 1.0] |
Координати текстури можуть містити від однієї до чотирьох координат. Зазвичай вони позначаються як s-, t-, r -, q- координати (таке позначення вирізняє їх від звичайних геометричних). Координати текстури визначаються командами glTexCoord*():
void glTexCoord [1 2 3 4] [s i f d] (TYPE coords);
void glTexCoord [1 2 3 4] [s i f d] v (TYPE *coords);
Дані команди використовуються для встановлення поточних координат текстури як частина даних, асоційованих з вершинами багатокутника. glTexCoord*() використовується разом із наступним викликом команди glVertex*(). Координати задаються або у явному вигляді, або у вигляді вектора. Зазвичай порядок побудови координат текстури багатокутника вказується у тій самій послідовності, що і координати вершин:
glBegin(GL_POLYGON);
glTexCoord2i(0, 0); glVertex3i(4, -2, 0); // координати вказані у порядку,
glTexCoord2i(0, 1); glVertex3i(4, 4, 0); // що відповідає обходженню
glTexCoord2i(1, 1); glVertex3i(0, 4, 0); // контуру за напрямом
glTexCoord2i(1, 0); glVertex3i(0, -2, 0); // годинникової стрілки
glEnd();
Інколи під час визначення текстур вказують параметри взаємодії текстури з фрагментом об’єкта. З цією метою OpenGL реалізує команди glTexEnv*():
void glTexEnv [i f] (GLenum target, GLenum pname, GLtype param);
void glTexEnv [i f] v (GLenum target, GLenum pname, GLtype *params);
де target визначає конфігурацію текстури і завжди дорівнює GL_TEXTURE_ENV, pname – символічне ім’я параметра конфігурації текстури із значенням GL_TEXTURE_EN_MODE, param – символічна константа із значеннями GL_MODULATE, GL_DECAL та GL_BLEND, params – покажчик на масив параметрів типу param.
Розглянемо приклад програми із побудовою текстур. У програмі будуватиметься призма, до якої застосовується накладення текстури у вигляді шахової дошки. Через те, що у програмі використовується лише одна текстура, текстурний об’єкт окремо не визначається.