Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Строение плоских механизмов по Л. В. АССУРУ
|
|
Профессор Л. В. Ассур в 1914-1918 гг. сформулировал принципы создания и исследования плоских рычажных механизмов с низшими парами.
 Основная идея Л.В. Ассура состоит в том, что любой плоский механизм может быть создан путем присоединения к начальному звену (или начальным звеньям) и стойке кинематических цепей нулевой подвижности, называемых структурными группами (группами Ассура).
Основная идея Л.В. Ассура состоит в том, что любой плоский механизм может быть создан путем присоединения к начальному звену (или начальным звеньям) и стойке кинематических цепей нулевой подвижности, называемых структурными группами (группами Ассура).
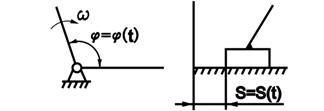
По классификации И. И Артобо-левского начальное звено и стойка, образующие одноподвижную кинематическую, являются механизмом 1-ого класса (рис. 1.4).
Рис 1.4. Механизмы первого класса
|
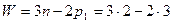 , если свободные элементы присоединить к стойке (рис. 1.5 б). В этом случае группа превращается в ферму.
, если свободные элементы присоединить к стойке (рис. 1.5 б). В этом случае группа превращается в ферму.
Для групп Ассура характерно определенное соотношение между числом звеньев и кинематических пар для групп только с одноподвижными парами
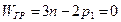 , т.е.
, т.е. 
На рис. 1.5 представлены механизмы, образованные подсоединением к механизму 1-ого класса и стойке групп Ассура.
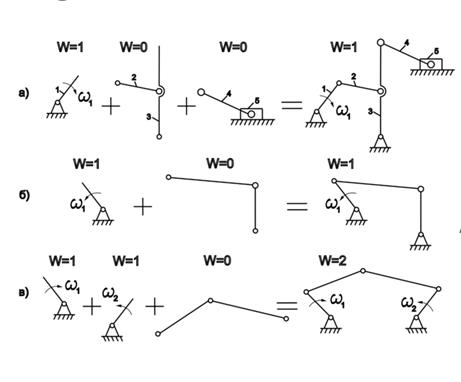
Рис. 1.5 Порядок образования механизмов.
Поскольку WГР = 0, степень подвижности механизма равна числу начальных (ведущих звеньев) или числу механизмов 1-ого класса. Например, для механизмов, представленных на рис. 1.5 а и б, W=1+0=1. При двух механизмах 1-ого класса и одной присоединенной группе (рис. 1.7 в) W=1+0+1=2.
Класс группы определяется наивысшим по классу контуром, входящим в ее состав.
Класс контура зависит от числа кинематических пар, входящих в контур.
 Порядок группы определяется числом свободных элементов, количеством внешних кинематических пар, которыми группа присоединяется к механизму.
Порядок группы определяется числом свободных элементов, количеством внешних кинематических пар, которыми группа присоединяется к механизму.

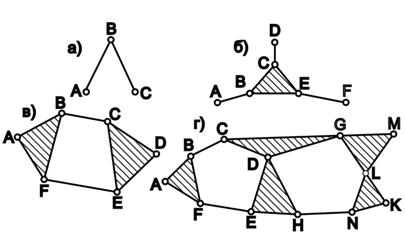
На рис. 1.6 представлены группы Ассура различных классов. Звеньями этих групп образованны контуры:
в группе ABC (рис.1.10 а) – контур АВ или ВС содержит 2 кинематические пары, следовательно, является контуром 2–ого класса;
в группе ABCDEF (рис.1.10 б) – контур BCD 3 – его класса;
в группе ABGDEF (рис. 1.10 в) – контур BCEF 4 – ого класса;
в группе ABCDEFGHKLMN (рис 1.10 г) можно отыскать два контура 5–ого класса BCDEF и DGLNH, которые содержат по 5 кинематических пар.
Сочетание чисел n = 2 и р1 = 3 характерно для структурных групп 2–ого класса, сочетание n = 4, р1 = 6 при наличии трех поводков и одного базисного звена – для групп 3–ого класса.
В практике синтеза механизмов наибольшее распространение получили группы 2-ого класса. В зависимости от числа и взаимного расположения вращательных и поступательных кинематических пар различают 5 видов структурных групп 2–ого класса (см. табл. 1.3).
Таблица 1.3
Виды групп Ассура 2-ого класса
| № вида | Схема группы | Вид и расположение пар | Пример образованных механизмов | Название механизма |
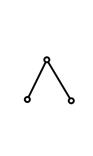
| Все пары вращательные | 
| Шарнирный четырехзвенник | |
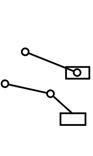
| Две пары вращательные | 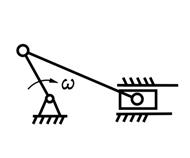
| Кривошипно-ползунный | |
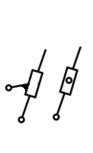
| Две пары вращательные | 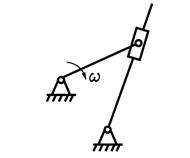
| Кулисный | |

| Две пары поступательные, одна вращательная | 
| Кулисно-ползунный (тангенсный) | |

| Две пары поступательные, одна вращательная | 
| Механизм двойного ползуна (синусный) |
Ниже будут продемонстрированы алгоритмы расчетов, разработанных для отдельных групп Ассура используемых при кинематическом и силовом анализе механизмов.
Пассивные связи. Иногда при разработке конструкций механизма в схему для увеличения его жесткости или устранения неопределенности движения звеньев в некоторых положениях в кинематическую схему включают дополнительные звенья, которые фактически не оказывают влияния на его кинематику. Например, на рис. 1.7 а представлен сдвоенный параллелограмм, в схему которого введено дополнительное звено CD=AB (ОА = BE, AC = CD). По формуле Чебышева имеем:  .
.
В действительности W=1, т.к. дополнительное звено в силу особого выбора размеров звеньев (фигуры ACDB и ОАВЕ являются параллелограммами) не налагается новых связей. Такие звенья и кинематические, которые они образуют, называют пассивными условиями связи.


Лишние степени свободы. У кулачкового механизма (рис. 1.7 б) по формуле Чебышева 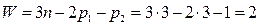 , хотя движение толкателя 3 полностью определяется движением кулачковой шайбы 1. Лишняя степень свободы появилась из-за возможности произвольного вращения ролика 2 вокруг своей оси. Она не влияет на кинематику толкателя. Введение в конструкцию ролика обусловлено необходимостью уменьшить трение, а, следовательно, и износ высшей кинематической пары.
, хотя движение толкателя 3 полностью определяется движением кулачковой шайбы 1. Лишняя степень свободы появилась из-за возможности произвольного вращения ролика 2 вокруг своей оси. Она не влияет на кинематику толкателя. Введение в конструкцию ролика обусловлено необходимостью уменьшить трение, а, следовательно, и износ высшей кинематической пары.
При решении задач структурного, кинематического и точностного анализа механизмов с высшими парами, а также выявления в них степеней свободы используют прием условной замены высшей пары кинематической цепью с низшими парами. Механизм, полученный в результате замены, называют заменяющим.
Условием замены является структурная (степени свободы исходного и заменяющего механизмов одинаковы) и кинетическая (сохранение относительного движения звеньев, составляющих высшую пару) эквивалентность.
В плоском механизме структурная эквивалентность соблюдается, если одна высшая пара заменяется одним дополнительным звеном, входящим в две дополнительные низшие пары со звеньями, образующими высшую пару. Для обеспечения кинематической эквивалентности необходимо, дополнительные низшие вращательные кинематические пары располагать в центрах кривизны звеньев, образующих высшую пару.
Примеры заменяющих механизмов представлены на рис. 1.8.