
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретичні відомості. Нехай радіус-вектор точки, що рухається по колу навколо нерухомої в даній системі відліку вісі , зробив за час dt нескінченно малий поворот.
|
|
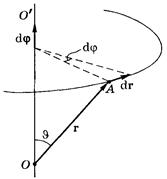 Нехай радіус-вектор точки, що рухається по колу навколо нерухомої в даній системі відліку вісі
Нехай радіус-вектор точки, що рухається по колу навколо нерухомої в даній системі відліку вісі 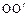 , зробив за час dt нескінченно малий поворот.
, зробив за час dt нескінченно малий поворот.
Кут повороту dj будемо характеризувати вектором 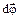 , модуль якого дорівнює dj, а напрямок збігається з віссю
, модуль якого дорівнює dj, а напрямок збігається з віссю 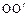 так, що напрямок повороту відповідає правилу " правило гвинта". Визначимо переміщення т. А за проміжок часу dt.
так, що напрямок повороту відповідає правилу " правило гвинта". Визначимо переміщення т. А за проміжок часу dt.
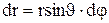
або у векторному вигляді 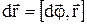 .
.
Кутовою швидкістю обертання тіла називається фізична векторна величина, яка дорівнює відношенню зміни кута повороту до проміжку часу, протягом якого ця зміна відбулася:
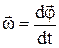 ,
, 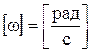 .
.
Напрямок 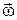 збігається з
збігається з 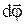 , тобто визначається правилом правого гвинта.
, тобто визначається правилом правого гвинта.
Кутовим прискоренням називається фізична векторна величина, яка дорівнює відношенню зміни кутової швидкості до проміжку часу, протягом якого ця зміна відбулася:
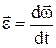 ,
, 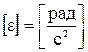 .
.
 Напрямок вектора
Напрямок вектора  збігається з напрямком
збігається з напрямком  . Запишемо формули
. Запишемо формули 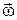 та
та  у проекціях на вісь Z, позитивний напрямок якої зв'яжемо з відліком координати j правилом правого гвинта:
у проекціях на вісь Z, позитивний напрямок якої зв'яжемо з відліком координати j правилом правого гвинта:
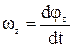 ,
, 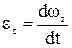 .
.
Визначимо залежність 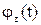 . Нехай
. Нехай 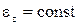 :
:
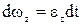 ,
, 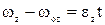 ,
, 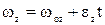 ,
,  ,
,
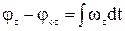 ,
, 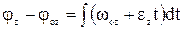 ,
, 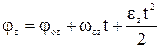
Останнє рівняння називається рівнянням обертального руху матеріальної точки.
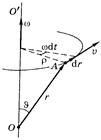 Визначимо швидкість довільної точки А, що обертається навколо нерухомої вісі ОО' з кутовою швидкістю w. Нехай положення точки А відносно деякої точки О вісі обертання характеризується радіусом-вектором
Визначимо швидкість довільної точки А, що обертається навколо нерухомої вісі ОО' з кутовою швидкістю w. Нехай положення точки А відносно деякої точки О вісі обертання характеризується радіусом-вектором 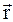 :
:
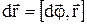 .
.
Розділимо обидві частини на dt:
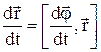 .
.
У підсумку одержуємо:
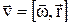
або
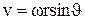 .
.
Але 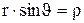 – радіус кола, по який рухається точка. Після відповідних замін одержуємо формулу, що зв'язує лінійну і кутову швидкості:
– радіус кола, по який рухається точка. Після відповідних замін одержуємо формулу, що зв'язує лінійну і кутову швидкості:
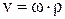 .
.
Визначимо повне прискорення точки: продиференціюємо формулу 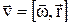 :
:
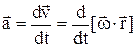 ,
, 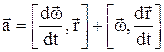
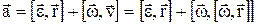 ,
, 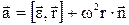 ,
,
де 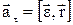 – тангенціальне прискорення,
– тангенціальне прискорення, 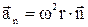 – нормальне прискорення.
– нормальне прискорення.
Повне прискорення:
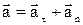 .
.
Модуль повного прискорення
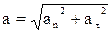 .
.
Динаміка – розділ механіки, у якому розглядаються причини, що обумовлюють той чи інший характер руху тіла. В основу динаміки покладені 3 закони Ньютона.
І-й закон (Закон інерції Галилея): Існують такі системи відліку, відносно яких тіло, що рухається поступально, зберігає свою швидкість постійною, якщо на нього не діють інші тіла чи дія інших тіл компенсується.
Інерція – явище збереження швидкості тіла при відсутності зовнішніх впливів.
Системи відліку, у яких виконується явища інерції, називаються інерціальними. Для інерціальних систем відліку справедливий принцип відносності Галілея, згідно якого всі інерціальні СВ за своїми механічними властивостями еквіваленти одна іншій. Інакше кажучи, у всіх ІСВ всі закони механіки виконуються однаково.
Основні динамічні характеристики:
- Сила – векторна фізична величина, яка є кількісною мірою взаємодії тіл. Сила визначена, якщо задані її модуль, напрямок і точка дотикання.
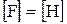
- Рівнодіючою силою називається сила, що діє на тіло так само, як і всі сили, прикладені до нього. Вона дорівнює векторній сумі всіх сил, що діють на тіло. 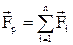 . При дії сили тіло змінює свою швидкість або деформується.
. При дії сили тіло змінює свою швидкість або деформується.
- Маса – фізична величина, що є кількісною мірою інертності тіл. 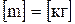 .
.
- Інертність – властивість тіл, яка полягає у тім, що для зміни швидкості тіл потрібно якийсь час, чим більше цей час, тим більше інертне тіло.
Властивості маси:
а) адитивність, тобто маса складеного тіла дорівнює сумі мас окремих його частин;
б) маса тіла як цілого – величина постійна, що не змінюється при його русі.
- Імпульс чи тіла кількість руху – фізична величина, яка дорівнює добутку маси тіла на його швидкість. Напрямок 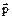 збігається з напрямком
збігається з напрямком 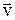 .
.
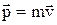
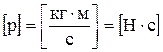 .
.
- Імпульс сили – фізична величина, яка дорівнює добутку сили на час дії сили: 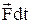 ,
, 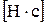 .
.