Решение. Элементы векторной алгебры аналитической геометрии и линейной алгебры.

Контрольная работа №1

Элементы векторной алгебры аналитической геометрии и линейной алгебры.

Вариант 2

1.1.2. Найти косинус угла между векторам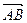и и 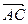, если А(3; 0; 1); В(5; -2; 2), С(-1; -3; 1). Сделать чертеж.

Решение.

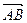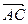
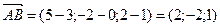Найдем векторы и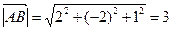

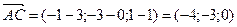и

и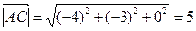

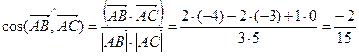
Ответ: -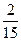

2.1.12 Даны уравнения одной из сторон ромба х-3у+10=0 и одной из ее диагоналей х+4у-4=0; диагонали ромба пересекаются в точке Р(0; 1). Найти уравнения остальных сторон ромба. Сделать чертеж.

Решение.

Пусть АВ сторона ромба ABCD лежит на прямой х-3у+10=0.

Найдем т. А -точку пересечения стороны АВ с диагональю х+4у-4=0, для этого решим систему:

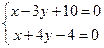т.А(-4; 2)

Диагонали ромба точкой пересечения делятся пополам, координаты т.С(х₁; y₁) находим по формулам середины отрезка:

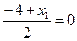
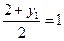
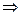х₁=4 у₁=0 т.С(4; 0)

Сторона CD||АВ, значит уравнение прямой CD: х-3у+m=0 (m - некоторое число)

Подставим в уравнение координаты т. С(4; 0): 4-0+m=0 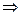m=-4 и х-3у-4=0 - уравнение стороны CD.

Найдем уравнение второй диагонали BD, т.к. BD 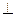АС и проходит через т.(0; 1), то уравнение ВD: 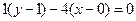или -4х+у-1=0.

Найдем координаты т.В, как точки пересечения прямых АВ: х-3у+10=0 и ВD: -4х+у-1=0.

Решим систему:

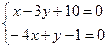т.В()

Тогда уравнение прямой ВС: 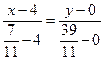или 39х+37у-156=0 – уравнение ВС

Cторона АD||BC, тогда уравнение АD: 39х+37у+n=0 (n - некоторое число). Подставим в уравнение координаты т.А(-4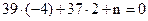; 2): n=82 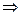39х+37у+82=0 уравнение стороны АD

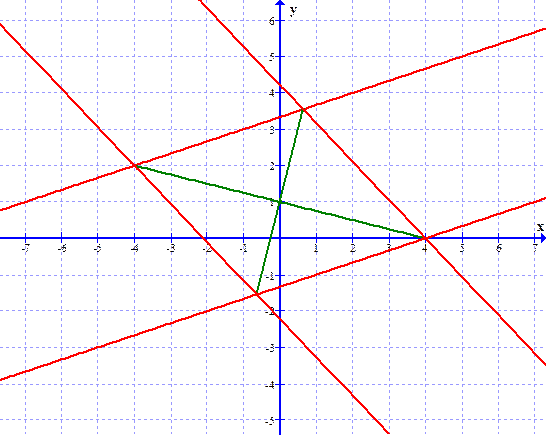
Ответ: АD: 39х+37у+82=0; ВС: 39х+37у-156=0; CD: х-3у-4=0.

С

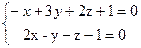
a) 3x+y–5z+1=0;

б) x-3y–5z+2=0;

в) -5x+y+3z=0;

г) -x+3y-5z+3=0;

д) 3х-у+5z–2=0.