Обратная матрица

Определение 1. Матрица В называется обратной для матрицы А, если

, (1)

где Е – единичная матрица.

Обозначение: .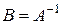

Теорема 1 (необходимые условия существования обратной матрицы). Для того, чтобы матрица А имела обратную она должна быть квадратной и невырожденной.

Доказательство. Ограничение на размерность матрицы следует из необходимого условия существования операции умножения матриц: количество столбцов первого сомножителя должно быть равно числу строк второго, а так как в данном случае еще накладывается и дополнительное условие коммутативности (1), то для его выполнения матрицы должны быть квадратными матрицами одного и того же размера.

Необходимость выполнения второго условия докажем методом от противного. Предположим, что нашлась матрица А, являющаяся вырожденной, т.е. 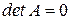, у которой существует обратная матрица В.

Тогда, с одной стороны, 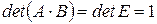, с другой стороны, 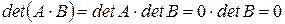. Получаем противоречие. Следовательно, предположение является неверным и матрица А – невырожденная. Теорема доказана.

Замечание. Таким образом, если у матрицы А существует обратная матрица, то она является квадратной матрицей того же размера, причем невырожденной.

Теорема 2 (единственность существования обратной матрицы). Если у матрицы существует обратная матрица, то она является единственной.

Доказательство. Применим метод от противного. Предположим, что нашлась матрица А для которой существуют две различные обратные матрицы В и С:

, .

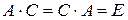Тогда, так как 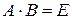, то умножая обе части равенства слева на матрицу, получаем

, , , .

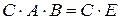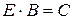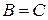И этого следует, что матрицы А и В – равные. Противоречие. Следовательно, если у матрицы существует обратная, то она единственная. Теорема доказана.

Теорема 3 (формула для вычисления обратной матрицы). Если квадратная матрица 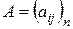является невырожденной, т.е. 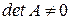, то обратная матрица 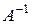может быть определена по правилу:

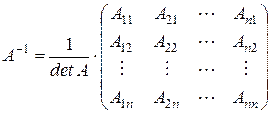, (2)

где 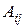- алгебраические дополнения к элементам 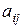, 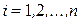; 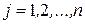матрицы .

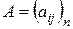Доказательство. Для доказательства утверждения достаточно показать выполнение условия (1).

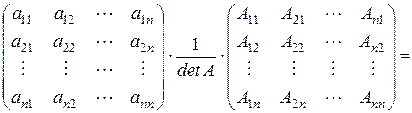
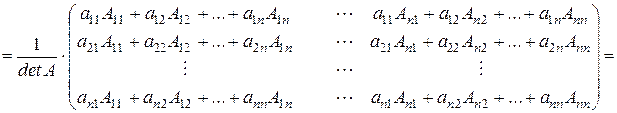
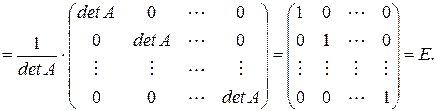
Так как согласно свойствам алгебраических дополнений к элементам матрицы (смотрите пункт 4):

; .

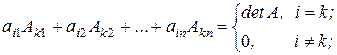
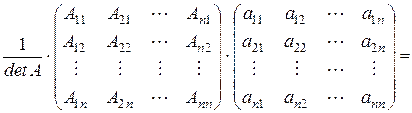
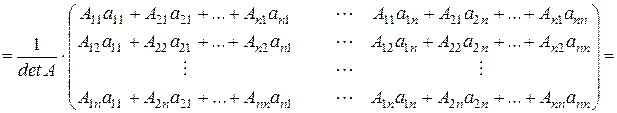
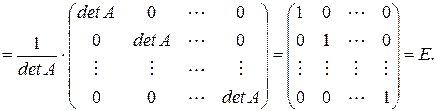
Так как, согласно свойствам алгебраических дополнений к элементам матрицы (смотрите пункт 4):

; .

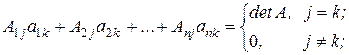
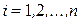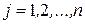Таким образом, условия определения 1 выполняются. Теорема доказана.

Замечание. Обратите внимание, что в формуле (2) алгебраические дополнения к элементам строк исходной матрицы А являются элементами столбцов матрицы, определяющей результат. Авторы некоторых учебников для облегчения запоминания формулы (2) вводят дополнительную матрицу 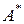, которая состоит из алгебраических дополнений к элементам матрицы А: 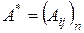и называется присоединенной матрицей для матрицы А. В этом случае формула (2) приобретает вид:

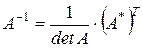. (3)

Но особой необходимости в этом нет.

Пример 1. Для матрицы 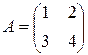найдите обратную матрицу.