
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Сначала вычислим определитель матрица А.
|
|
Сначала вычислим определитель матрица А.
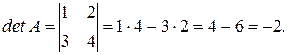
Он отличен от нуля, следовательно, у матрицы существует обратная матрица и для её определения достаточно определить алгебраические дополнения к элементам.
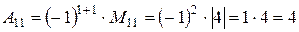 ;
;
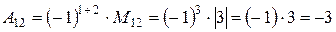 ;
;
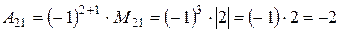 ;
;
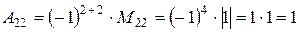 .
.
Согласно формуле (2),
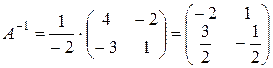 .
.
Замечание. Как видно из рассмотренного примера особой необходимости в формуле (3) нет, нужно только правильно расставить алгебраические дополнения к строкам, разместив их в столбцы.
Пример 2. Решите матричное уравнение: 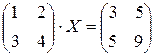 .
.
Решение. Данное уравнение можно решить двумя способами.
1 способ. Заметив, что матрица Х – квадратная матрица второго порядка, вводим четыре неизвестных 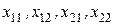 , соответствующих её элементам:
, соответствующих её элементам: 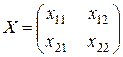 , и, расписывая произведение матриц, стоящих в левой части исходного равенства:
, и, расписывая произведение матриц, стоящих в левой части исходного равенства:
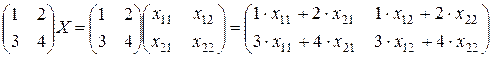 ,
,
получаем:
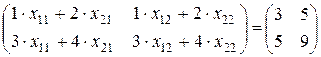 ,
,
что приводит нас к системе четырех уравнений с четырьмя неизвестными:
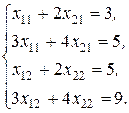
Данная система распадается на две системы с двумя неизвестными:
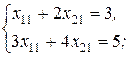 и
и 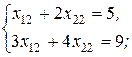 решая которые получаем:
решая которые получаем:
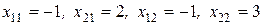 .
.
2 способ. Введем обозначения: 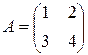 и
и 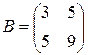 , тогда исследуемое уравнение примет вид:
, тогда исследуемое уравнение примет вид:
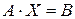 . (4)
. (4)
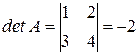 (смотрите расчеты в примере 1), следовательно, у неё существует обратная матрица, поэтому, умножая обе части равенства (4) слева на
(смотрите расчеты в примере 1), следовательно, у неё существует обратная матрица, поэтому, умножая обе части равенства (4) слева на 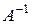 получаем, что
получаем, что
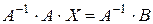 ,
,
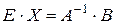 ,
,
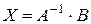 .
.
Матрицу 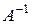 мы уже определили выше (см. Пример 1):
мы уже определили выше (см. Пример 1): 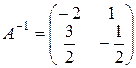 .
.
Следовательно,
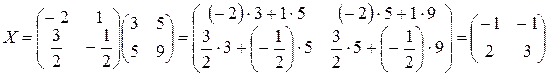 .
.
В практических приложениях достаточно часто используются свойства обратной матрицы, которые представлены в теореме 4.
Теорема 4 (свойства обратной матрицы)
1) 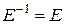 . (5)
. (5)
2) 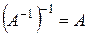 . (6)
. (6)
3) 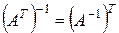 . (7)
. (7)
4) 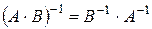 , (8)
, (8)
для невырожденных матриц А и В одного порядка.
5) 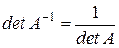 . (9)
. (9)