Линейные подпространства

Пусть задано некоторое линейное пространство L над некоторым полем P.

Определение 1. Подмножество М линейного пространства L называется линейным подпространством этого пространства, если оно само является линейным пространством по отношению к определенным в L операциям сложения векторов и умножения векторов на число из поля Р.

Например, множество векторов фиксированной прямой, исходящих из одной точки этой прямой, - подпространство множества векторов плоскости, (содержащей данную прямую), исходящих из той же точки (над полем R).

Теорема 1 (достаточные условия, К., стр. 201) Для того, чтобы непустое подмножество М линейного пространства L было его линейным подпространством, достаточно выполнения следующих требований:

1) если , то ;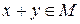

2) если 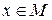, то .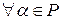

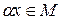Доказательство. Для доказательства данного утверждения достаточно показать, что в этом случае выполняются аксиомы 1 – 8 из определения линейного пространства. Действительно.

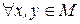
1) 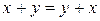, т.к. 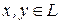, а для них эти условия выполняются.

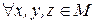
2) 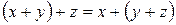, т.к. 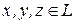, а для них эти условия выполняются.

3) Существует нулевой элемент 0, т.к. .

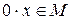4) Для существует противоположный элемент, так как .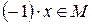

5) 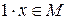, а значит, 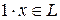и 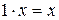, согласно соответствующему свойству L.

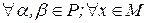
6) 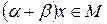, значит, 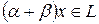, и согласно свойствам пространства L: .

Аналогично доказывается (проделайте это самостоятельно) выполнение аксиом 7 и 8:

7) ;

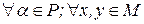
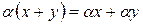8) .

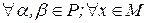
Теорема доказана.

Задание 1. Докажите выполнение аксиом 7 и 8.