Следствие 1. - линейное подпространство L.

Доказательство. Утверждение является очевидным, так как автоматически выполняются как условия определения, так и условия теоремы 1.

Определение 2. Множество 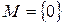, состоящее из одного нулевого вектора пространства L, называется нулевым подпространством.

Следствие 2. 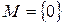- линейное подпространство L(К., стр. 202).

Доказательство. Проведите самостоятельно.

Следствие 3. Если 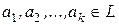, то множество 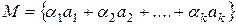, где 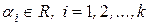; - линейное подпространство пространства L.

Доказательство (К, стр. 202). Пусть . Тогда, учитывая способ задания пространства M, получаем, что если

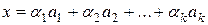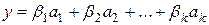, , то

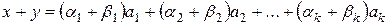и, значит, .

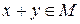Аналогично, 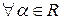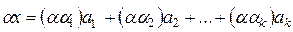, т.е. 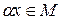. Условия теоремы 1 выполняются, следовательно, М – линейное подпространство пространства L. Утверждение доказано.

Замечание. Если линейное подпространство М задается как линейная комбинация векторов 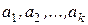, то говорят (К., стр. 202), что линейное подпространство порождено системой векторов .

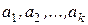Более того, всякое линейное подпространство конечномерного линейного пространства порождается конечной системой векторов, причем, если оно не является нулевым, то в нем можно выбрать базис, причем число векторов в этом базисе не превышает размерности исходного линейного пространства. Размерность нулевого подпространства полагают равной нулю. Это позволяет сформулировать следующее следствие.

Следствие 4. Если 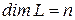и M – линейное подпространство линейного пространства L, то 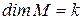, где 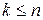, причем 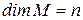, если 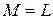и , если .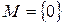

Задание 2. Докажите следствия 2 и 4.

Следствие 5. Если 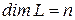, то для 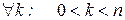существует линейное подпространство М, такое что .

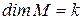Доказательство. Достаточно взять любые к линейно независимых векторов пространства L и рассмотреть множество их линейных комбинаций.

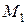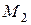Пусть и - линейные подпространства пространства линейного пространства L.

Определение 3. Множество 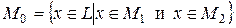называется пересечением линейных подпространств 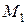и 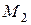(К, стр. 202)

Обозначение: .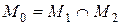

Определение 4. Множество 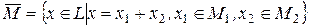называется суммой линейных подпространств 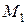и 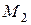(К, стр. 202).

Обозначение: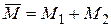

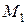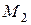Следствие 6. Если и - линейные подпространства линейного пространства L, то пересечение и сумма этих подпространств – линейные подпространства линейного пространства L.

Доказательство. Доказательство проведите самостоятельно.

Задание 3. Докажите следствие 6.

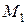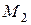Следствие 7. Если и - линейные подпространства линейного пространства L, причем,

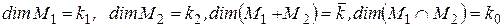, то

, (1)

т.е. .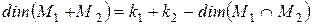

Доказательство (К, стр. 203).Для доказательства формулы (1) поступим следующим образом. Зафиксируем произвольным образом какой-нибудь базис 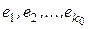линейного подпространства 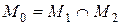и дополним его до базисов линейных подпространств 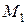и 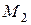, соответственно: 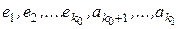- базис подпространства 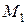, 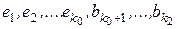- базис подпространства .

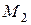В этом случае, согласно определению пространства 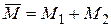, следует, что оно порождается системой векторов 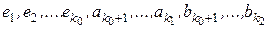, состоящей из 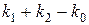векторов.

Для доказательства справедливости формулы (1) достаточно доказать, что векторы 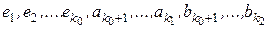линейно независимы.

Предположим противное, т.е. что векторы – линейно зависимы, тогда найдется нетривиальный набор коэффициентов 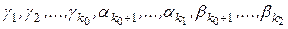при котором линейная комбинация этих векторов обращается в нуль:

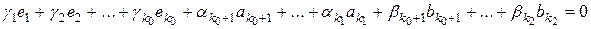. (2)

Тогда

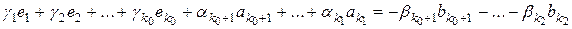. (3)

Так как левая часть равенства (3) – линейная комбинация векторов подпространства 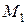, а правая часть – линейная комбинация векторов подпространства , то найдется вектор d, одновременно принадлежащи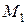й и , такой, что может быть представлен разложением как по базису подпространства :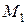

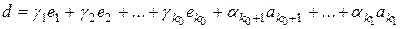, (4)

так и по базису пространства :

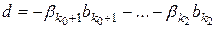. (5)

С другой стороны, так как вектор одновременно принадлежит 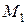и , то он является вектором пространства 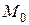, т.е. разлагается по базису подпространства 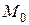, т.е. найдется некоторый набор коэффициентов 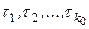, при котором

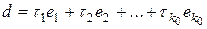. (6)

Из (4) и (6) следует, что

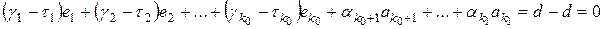. (7)

Так как векторы 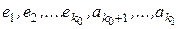образуют базис, то они линейно независимы и, следовательно, равенство (7) возможно лишь при нулевом наборе коэффициентов, т.е.

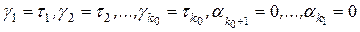. (8)

Из (8) следует, что в этом случае исходное равенство (2) приобретает вид:

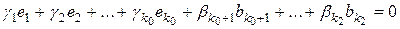. (9)

Так как векторы 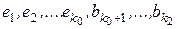, представляющие базис подпространства 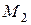, - линейно независимые векторы, то равенство (9) возможно только при тривиальном наборе коэффициентов. Следовательно,

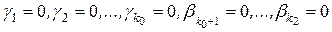. (10)

Из (8) и (10) следует, что равенство (2) возможно только при тривиальном наборе коэффициентов. Значит, предположение о линейной зависимости векторов 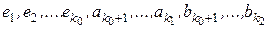является неверным, т.е. они линейно независимы. Утверждение доказано.

Замечание. Следствие 7 доказано в предположении, что размерность пересечения . Формула (1) сохраняет свой вид и в том случае, когда 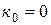, т.е. когда пересечение подпространств является нулевым подпространством. Проверьте это самостоятельно.