
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Доказательство. Пусть в конечномерном линейном пространстве L, размерности n, зафиксирован базис и задано линейное преобразование А.
|
|
Пусть в конечномерном линейном пространстве L, размерности n, зафиксирован базис 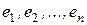 и задано линейное преобразование А.
и задано линейное преобразование А.
Пусть 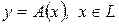 , где
, где 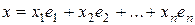 ,
, 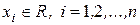 , тогда, поскольку
, тогда, поскольку  , то
, то 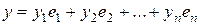 ,
, 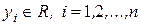 .
.
С другой стороны, в силу линейности преобразования А,
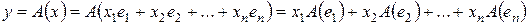 .
.
Так как 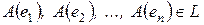 , то они так же могут быть разложены по базису
, то они так же могут быть разложены по базису 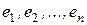 .
.
Пусть 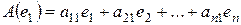 ,
,
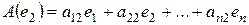 ,
,
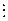
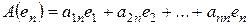 .
.
Тогда, подставляя эти разложения в полученное выше представление для вектора у, получаем:
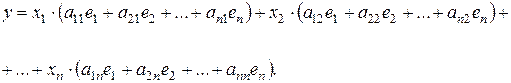
Выделяя коэффициенты при базисных векторах 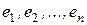 , приходим к равенству:
, приходим к равенству:
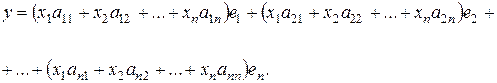
В силу единственности разложения вектора у по базису 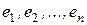 приходим к системе:
приходим к системе:
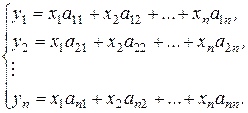
Вводя матрицы 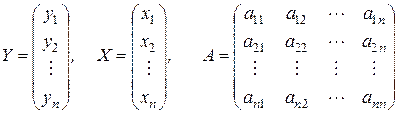 ,
,
систему можно представить в виде матричного уравнения:
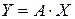 .
.
Данное уравнение позволяет при известных матрице А и столбце координат Х вектора х найти столбец координат У вектора у. Единственность следует из единственности разложения образов базисных векторов и исходного вектора х по базису.
Определение 3. Матрица 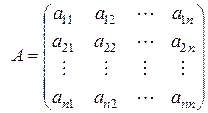 , столбцы которой – координаты образов базисных векторов
, столбцы которой – координаты образов базисных векторов 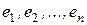 при преобразовании А, называется матрицей линейного преобразования в базисе
при преобразовании А, называется матрицей линейного преобразования в базисе 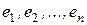 .
.
Замечание. В тоже время, наоборот, в конечномерном линейном пространстве L, размерности n, с фиксированным базисом, каждой квадратной матрице 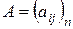 можно поставить в соответствие преобразование по правилу: если X - столбец координат вектора х в выбранном базисе, то
можно поставить в соответствие преобразование по правилу: если X - столбец координат вектора х в выбранном базисе, то 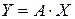 - столбец координат вектора у в этом базисе, где
- столбец координат вектора у в этом базисе, где 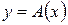 .
.
Более того, данное преобразование будет линейным. Действительно.
1) Если столбец координат вектора х – Х, столбец координат вектора у – У, то столбец координат вектора 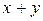 -
- 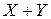 . Столбец координат вектора
. Столбец координат вектора  , вектора
, вектора 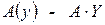 , вектора
, вектора 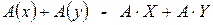 , вектора
, вектора 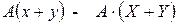 . Так как
. Так как  , то свойство
, то свойство 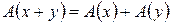 выполняется.
выполняется.
2) Если столбец координат вектора х - Х, то столбец координат вектора 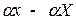 . Столбец координат вектора
. Столбец координат вектора  , вектора
, вектора 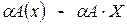 , вектора
, вектора 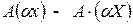 . Так как
. Так как 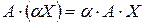 , то свойство
, то свойство 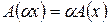 выполняется.
выполняется.
Таким образом, в конечномерном линейном пространстве L, размерности n, с фиксированным базисом существует взаимно однозначное соответствие между линейными преобразованиями и квадратными матрицами размерности n.
Как уже было отмечено выше, в конечномерном линейном пространстве вид матрицы линейного преобразования зависит от выбора базиса.
Выведем формулы для связи матриц линейного преобразования в двух базисах одного и того же конечномерного линейного пространства.
Пусть задано линейное пространство L размерности n, в котором заданы два базиса 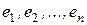 и
и 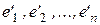 , причем, известна матрица Т перехода от базиса
, причем, известна матрица Т перехода от базиса 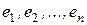 к базису
к базису 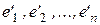 .
.
Пусть линейное преобразование A в базисе 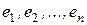 имеет матрицу
имеет матрицу 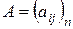 , а в базисе
, а в базисе 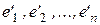 - матрицу
- матрицу 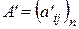 .
.
Пусть 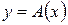 , где
, где  – столбцы координат векторов х, у в базисе
– столбцы координат векторов х, у в базисе 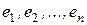 ;
; 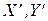 - столбцы координат векторов х, у в базисе
- столбцы координат векторов х, у в базисе 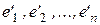 .
.
В базисе 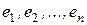
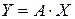 .
.
Учитывая связь координат векторов х и у в базисах 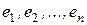 и
и 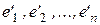 :
:
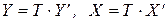 ,
,
получаем, что 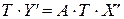 .
.
Так как матрица перехода Т – невырожденная, то у неё существует обратная матрица 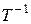 . Умножая обе части получившегося равенства слева на
. Умножая обе части получившегося равенства слева на 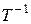 , имеем:
, имеем:
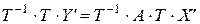 ,
,
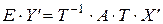 ,
,
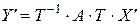 .
.
С дугой стороны, в базисе 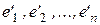
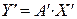 , следовательно,
, следовательно,
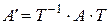 .
.
Нетрудно заметить (проделайте соответствующие выкладки самостоятельно), что
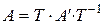 .
.
Теорема 2. Величина определителя матрицы линейного преобразования в конечномерном линейном пространстве не зависит от выбора базиса, т.е. является инвариантной величиной относительно базиса.
Доказательство. Пусть в конечномерном линейном пространстве L размерности n задано некоторое линейное преобразование A.
Зафиксируем в этом пространстве произвольным образом два базиса 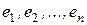 и
и 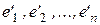 .
.
Пусть А и 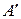 - матрицы линейного преобразования А в базисах
- матрицы линейного преобразования А в базисах 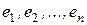 и
и 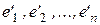 , соответственно.
, соответственно.
По доказанному выше, матрицы линейного преобразования в этом случае связаны по правилу: 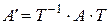 , где Т – матрица перехода от базиса
, где Т – матрица перехода от базиса 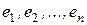 к базису
к базису 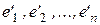 . Анализируя величину определителя матрицы
. Анализируя величину определителя матрицы 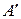 , получаем:
, получаем:
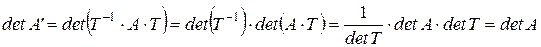 .
.
В силу произвольности выбора базисов результат будет справедлив для любых базисов, следовательно, величина матрицы линейного преобразования не зависит от базиса. Теорема доказана.
Нетрудно заметить, что для любого линейного преобразования А в любом линейном пространстве L 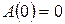 , так как
, так как 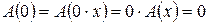 .
.
Определение 4. Линейное преобразование А называется невырожденным, если 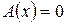 , только при
, только при 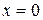 . В противном случае, если найдется ненулевой элемент
. В противном случае, если найдется ненулевой элемент 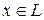 , такой что
, такой что 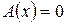 , линейное преобразование называется вырожденным.
, линейное преобразование называется вырожденным.
Теорема 3. В конечномерном линейном пространстве L линейное преобразование A является невырожденным тогда и только тогда, когда матрица линейного преобразования является невырожденной.
Доказательство. Так как величина определителя матрицы линейного преобразования в конечномерном линейном пространстве не зависит от выбора базиса, то достаточно доказать справедливость этого утверждения для любого базиса.
Пусть 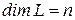 и
и 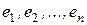 - некоторый фиксированный базис.
- некоторый фиксированный базис.
Пусть 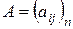 - матрица линейного преобразования А в базисе
- матрица линейного преобразования А в базисе 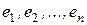 , Х – столбец координат вектора х в базисе
, Х – столбец координат вектора х в базисе 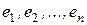 .
.
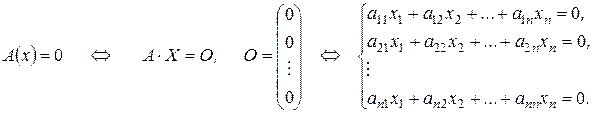
Очевидно, что 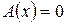 , только при
, только при 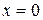 , тогда и только тогда, когда получившаяся система имеет только нулевое решение, а это возможно лишь тогда и только тогда, когда определитель системы равен нулю. Так как определитель системы – определитель матрицы линейного преобразования, то теорема доказана.
, тогда и только тогда, когда получившаяся система имеет только нулевое решение, а это возможно лишь тогда и только тогда, когда определитель системы равен нулю. Так как определитель системы – определитель матрицы линейного преобразования, то теорема доказана.
Следствие. В конечномерном линейном пространстве L линейное преобразование A является вырожденным тогда и только тогда, когда матрица линейного преобразования является вырожденной.
Доказательство. Справедливость этого утверждения следует из того, что система, полученная при доказательстве теоремы 3 имеет нетривиальное (ненулевое) решение тогда и только тогда, когда определитель, составленный из коэффициентов при неизвестных, равен нулю.
Определение 5. Линейное преобразование А называется тождественным, если 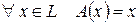 .
.
Очевидно, что в конечномерном линейном пространстве L, размерности n, в любом базисе 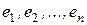 соответствует единичная матрица порядка n.
соответствует единичная матрица порядка n.
Действительно.
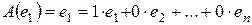 ,
,
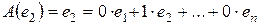 ,
,
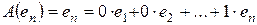 .
.
Следовательно, матрица линейного преобразования А в данном базисе имеет вид:
 .
.