Способы задания числовой последовательности

Методические указания

Определение 1. Функцию y = f(x), x N называют функцией натурального аргумента или числовой последовательностью и обозначают: y = f(n) или y₁, y₂, y₃,..., y_n,... или (y_n).

В данном случае независимая переменная – натуральное число.

Способы задания числовой последовательности

Словесный способ.

Правила задания последовательности описываются словами, без указания формул или когда закономерности между элементами последовательности нет.

Пример 1. Последовательность простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31,.....

Пример 2. Произвольный набор чисел: 1, 4, 12, 25, 26, 33, 39,....

Пример 3. Последовательность чётных чисел 2, 4, 6, 8, 10, 12, 14, 16,...

Аналитический способ.

Любой n-й элемент последовательности можно определить с помощью формулы.

Пример 1. Последовательность чётных чисел: y = 2n.

Пример 2. Последовательность квадрата натуральных чисел: y = n²;

1, 4, 9, 16, 25,..., n²,....

Пример 3. Стационарная последовательность: y = C; C, C, C,..., C,...

Частный случай: y = 5; 5, 5, 5,..., 5,....

Пример 4. Последовательность y = 2ⁿ;

2, 2², 2³, 2⁴,..., 2ⁿ,....

Рекуррентный способ.

Указывается правило, позволяющее вычислить n-й элемент последовательности, если известны её предыдущие элементы.

Пример 1. Арифметическая прогрессия: a₁=a, a_n+1=a_n+d, где a и d – заданные числа, d - разность арифметической прогрессии. Пусть a₁=5, d=0, 7, тогда арифметическая прогрессия будет иметь вид: 5; 5, 7; 6, 4; 7, 1; 7, 8; 8, 5;....

Пример 2. Геометрическая прогрессия: b₁= b, b_n+1= b_nq, где b и q – заданные числа, b 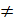0, q 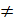0; q – знаменатель геометрической прогрессии. Пусть b₁=23, q=½, тогда геометрическая прогрессия будет иметь вид: 23; 11, 5; 5, 75; 2, 875;....

Пример 3. Последовательность Фибоначчи. Эта последовательность легко задаётся рекуррентно: y₁=1, y₂=1, y_n-2+y_n-1, если n=3, 4, 5, 6,.... Она будет иметь вид: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,....

Аналитически последовательность Фибоначчи задать трудно, но возможно. Формула, по которой определяется любой элемент этой последовательности, выглядит так:

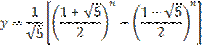
Пример 1. Составить возможную формулу n-го элемента последовательности (y_n):

а) 1, 3, 5, 7, 9, 11,...;

б) 4, 8, 12, 16, 20,...;

Решение.

а) Это последовательность нечётных чисел. Аналитически эту последовательность можно задать формулой y = 2n+1.

б) Это числовая последовательность, у которой последующий элемент больше предыдущего на 4. Аналитически эту последовательность можно задать формулой y = 4n.

Пример 2. Выписать первые десять элементов последовательности, заданной рекуррентно: y₁=1, y₂=2, y_n = y_n-2+y_n-1, если n = 3, 4, 5, 6,....

Решение.

Каждый последующий элемент этой последовательности равен сумме двух предыдущих элементов.

y₁=1;

y₂=2;

y₃=1+2=3;

y₄=2+3=5;

y₅=3+5=8;

y₆=5+8=13;

y₇=8+13=21;

y₈=13+21=34;

y₉=21+34=55;

y₁₀=34+55=89.

Пример 3. Последовательность (y_n) задана рекуррентно: y₁=1, y₂=2, y_n=5y_n-1- 6y_n-2. Задать эту последовательность аналитически.

Решение.

Найдём несколько первых элементов последовательности.

y₁=1;

y₂=2;

y₃=5y₂-6y₁=10-6=4;

y₄=5y₃-6y₂=20-12=8;

y₅=5y₄-6y₃=40-24=16;

y₆=5y₅-6y₄=80-48=32;

y₇=5y₆-6y₅=160-96=64.

Получаем последовательность: 1; 2; 4; 8; 16; 32; 64;..., которую можно представить в виде

2⁰; 2¹; 2²; 2³; 2⁴; 2⁵; 2⁶....

n = 1; 2; 3; 4; 5; 6; 7....

Анализируя последовательность, получаем следующую закономерность: y = 2^n-1.