
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методические указания. 1. Богомолов Н.В. Практические занятия по математике
|
|
Литература.
1. Богомолов Н.В. Практические занятия по математике. –М.: Высш.шк., 2009
Методические указания.
Пример 1. Найдите производную функции: 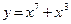 ; 2)
; 2) 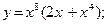 3)
3) 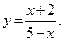
Решение
1) 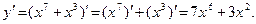 2)
2) 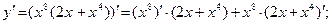 Учитывая, что
Учитывая, что  ; ;  имеем имеем
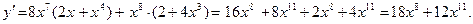 3)
3) 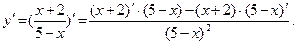 Учитывая, что
Учитывая, что  имеем имеем

| Пояснения
В задании 1 надо найти производную суммы по формуле  ;
в задании 2 – производную произведения ;
в задании 2 – производную произведения  в задании 3 – производную частного в задании 3 – производную частного  Также в заданиях 1 и 2 следует использовать формулу
Также в заданиях 1 и 2 следует использовать формулу 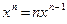 , а в задании 2 учесть, что при вычислении производной 2 x постоянный множитель 2 можно вынести за знак производной. , а в задании 2 учесть, что при вычислении производной 2 x постоянный множитель 2 можно вынести за знак производной.
|
Пример 2. Вычислите значение производной функции 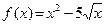 в точках х=4 и х=0, 01.
в точках х=4 и х=0, 01.
Решение
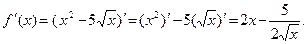
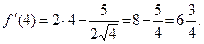
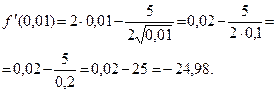
| Пояснения
Для нахождения производной в указанных точках достаточно найти производную данной функции и в полученное выражение подставить заданные значения аргумента. При вычислении производной следует учесть, что заданную разность можно рассматривать, как алгебраическую сумму выражений х 2 и  , а при нахождении производной , а при нахождении производной  за знак производной вынести постоянный множитель (- 5). за знак производной вынести постоянный множитель (- 5).
|
Пример 3. Найдите значения х, при которых производная функции  равна 0.
равна 0.
Решение
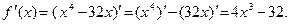
 Тогда Тогда 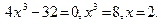 Ответ: х = 2.
Ответ: х = 2.
| Пояснения Чтобы найти соответствующие значения х, достаточно найти производную данной функции, приравнять её к нулю и решить полученное уравнение. |
Пример 4. Найдите производную функции: 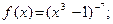 2)
2) 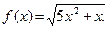
Решение
1)  Учитывая, что
Учитывая, что  получаем получаем 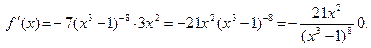

| Пояснения В заданиях 1 и 2 необходимо найти соответственно производную степени и корня, но в основании степени и под знаком корня стоит не аргумент х, а выражение с этим аргументом (тоже функция от х). Следовательно, необходимо найти производные сложных функций. |
2) Выполните задания.
Вариант