
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алгоритм Данцига
|
|
Одним із методів пошуку всіх найкоротших шляхів у зваженому орієнтованому графі є алгоритм Данцига. Його складність становить 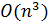 , де
, де 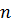 – кількість вершин графа. Розглянемо схему роботи алгоритму.
– кількість вершин графа. Розглянемо схему роботи алгоритму.
Перенумеруємо всі вершини графа числами від 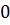 до
до 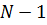 , де
, де  – розмірність графа, який віддзеркалює топологію мережі. Кожному ребру відповідає певний ваговий коефіцієнт. Якщо ребра немає, то значення коефіцієнта рівне нескінченності. Вихідними даними для алгоритму є матриця вагових коефіцієнтів. Ідея полягає в послідовному обчисленні за допомогою рекурентної процедури під матриць найкоротших шляхів
– розмірність графа, який віддзеркалює топологію мережі. Кожному ребру відповідає певний ваговий коефіцієнт. Якщо ребра немає, то значення коефіцієнта рівне нескінченності. Вихідними даними для алгоритму є матриця вагових коефіцієнтів. Ідея полягає в послідовному обчисленні за допомогою рекурентної процедури під матриць найкоротших шляхів 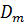 зростаючої розмірності
зростаючої розмірності 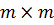 . Кожна така матриця, фактично, є матрицею найкоротших шляхів під графа з вершинами від
. Кожна така матриця, фактично, є матрицею найкоротших шляхів під графа з вершинами від 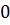 до
до  .
.
Деякі позначення:
 – розмірність графа, який віддзеркалює топологію мережі;
– розмірність графа, який віддзеркалює топологію мережі;
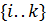 – множина цілих чисел від
– множина цілих чисел від 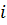 до
до 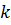 ;
;
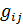 – довжина ребра з вершини
– довжина ребра з вершини 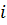 в
в  ;
;
 – довжина найкоротшого знайденого шляху з
– довжина найкоротшого знайденого шляху з 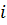 в
в  ;
;
 – шлях з вершини
– шлях з вершини 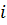 до
до  через вершину
через вершину 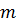 ;
;
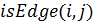 – предикат, значенням якого буде істина, якщо існує ребро з вершини
– предикат, значенням якого буде істина, якщо існує ребро з вершини 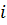 в
в  ;
;
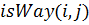 – предикат, значенням якого буде істина, якщо існує шлях з вершини
– предикат, значенням якого буде істина, якщо існує шлях з вершини 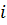 в
в  ;
;
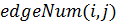 – кількість ребер на шляху з
– кількість ребер на шляху з 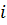 в
в  ;
;
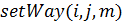 – встановлення шляху
– встановлення шляху  .
.