Теоретические сведения. Средняя скорость точки: , где ∆ - приращение радиус-вектора

Литература

1. Трофимова Т.И. Курс физики. 11-е изд., стер. - М.: Академия, 2006.— 560 с. Учебное пособие (9-е издание, переработанное и дополненное), 2004 г.

3. Трофимова Т.И., Фирсов А.В. Курс физики. Задачи и решения. Учеб. пособие для втузов/.- М.: Издат. Центр «Академия», 2004.-592.

4. Трофимова Т.И. Павлова З.Г. Сборник задач по курсу физики с решениями. М.: Высш. шк., 2002.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

§ 1. Кинематика

Средняя скорость точки: 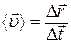, где ∆ 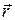- приращение радиус-вектора 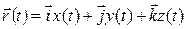за время ∆ t ( 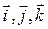- единичные векторы (орты) осей прямоугольной системы координат, 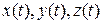- координаты точки).

Мгновенная скорость: .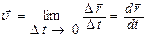

Модуль скорости: 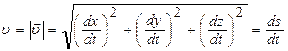, где ds – путь, пройденный точкой за время dt.

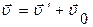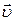Закон сложения скоростей Галилея: , где - скорость материальной точки в условно неподвижной системе координат (абсолютная скорость), 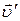- её скорость в движущейся системе координат (относительная скорость), 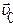- скорость подвижной системы координат относительно неподвижной (переносная скорость).

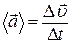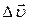Среднее ускорение точки: , где - приращение скорости за время 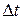. Мгновенное ускорение: .

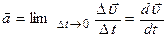Модуль ускорения: .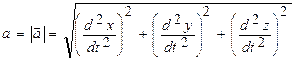

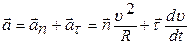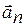Полное ускорение при плоском криволинейном движении: , где и 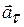- нормальное и тангенциальное ускорение, 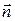и 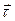- единичные векторы в направлении главной нормали и касательной к траектории, R – радиус кривизны траектории.

Направление вектора полного ускорения определяется из соотношения: 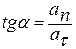, где 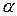- угол между векторами полного ускорения и скорости.

Угловая скорость и угловое ускорение при вращательном движении: .

Связь линейной и угловой скорости: 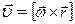, где 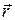- радиус-вектор рассматриваемой точки относительно любой точки оси вращения.

Связь угловой скорости с периодом 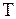и частотой вращения: .

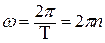Нормальное и тангенциальное ускорение точки вращающегося тела: 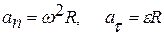, где R – расстояние от оси вращения.

Уравнение механических гармонических колебаний и его решение: 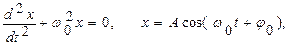где x – смещение, А – амплитуда, 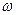₀ – собственная частота колебаний, 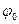- начальная фаза.

При сложении двух одинаково направленных гармонических колебаний одной и той же частоты: ,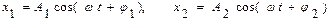

амплитуда и начальная фаза результирующего колебания определяется соотношением: , .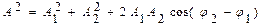

§ 2. Динамика материальной точки и системы материальных точек.

Основное уравнение динамики (второй закон Ньютона): 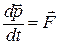, где 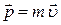- импульс частицы, m – её масса, 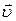- скорость.

Импульс системы равен сумме импульсов её отдельных частей: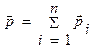

Поступательное движение системы 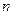- частиц как целого можно характеризовать движением одной точки – центра масс системы: 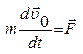, где 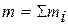- суммарная масса всех частиц рассматриваемой системы, 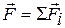- результирующая всех внешних сил, 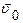- скорость движения центра масс (i=1, 2, 3…n).

Радиус – вектор, определяющий положение центра масс системы частиц в пространстве относительно произвольной точки 0: 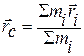, где m_i – масса i – частицы, 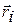- её радиус-вектор с началом в точке 0.

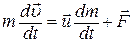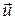Уравнение движения тела переменной массы: , где – скорость отделяемого (присоединяемого) вещества относительно движущегося тела.

Скорость ракеты (формула Циолковского): 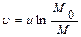, где u – скорость частиц относительно ракеты, М₀ и М – начальная и текущая массы ракеты.

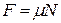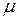Сила трения скольжения: , где - коэффициент трения, 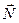- сила нормального давления.

§ 3. Законы сохранения энергии, импульса и момента импульса.

Элементарная работа силы 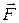на перемещении : .

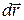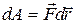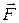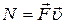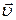Мощность постоянной силы : , где - скорость.

Работа сил поля равна убыли потенциальной энергии частицы в данном поле: .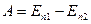

Приращение кинетической энергии частицы: 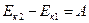, где А – работа результирующей всех сил, действующих на частицу.

Приращение полной механической энергии частицы в потенциальном поле: 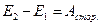, где А _{стор .} – алгебраическая сумма работ всех сторонних сил.

В замкнутой системе полный импульс не изменяется (закон сохранения импульса):

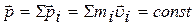
Момент силы 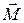относительно некоторой точки 0: 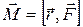, где 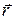- радиус-вектор, проведенный из точки 0 в точку приложения силы .

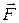Момент импульса частицы 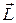относительно некоторой точки 0: 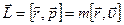, где 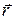- радиус-вектор, проведенный из точки 0 в точку, где находится частица, импульс частицы - .

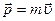Закон изменения момента импульса 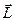системы: 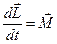, где 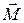- суммарный момент всех внешних сил.

Закон сохранения момента импульса: 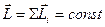, т.е. момент импульса замкнутой системы частиц остается постоянным.

§ 4. Механика твердого тела.

Уравнение динамики твердого тела, вращающегося вокруг неподвижной оси z: 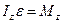, где M_z – алгебраическая сумма моментов внешних сил относительно оси z.

Момент инерции некоторых тел:
точки массой m на расстоянии R от оси вращения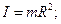
однородного стержня длинной l относительно оси, проходящей через его центр масс перпендикулярно стержню, m – масса стержня.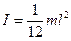
однородного стержня, ось вращения которого перпендикулярна стержню и проходит через его конец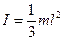
однородного диска или цилиндра радиусом R и массой m относительно оси, совпадающей с осью диска или цилиндра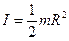
тонкостенной трубы или кольца относительно оси совпадающей с осью трубы или кольца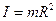
полого цилиндра массой m относительно оси симметрии. R1 и R2 - внутренний и внешний радиусы.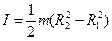
однородного шара массой m и радиусом R относительно оси, совпадающей с его диаметром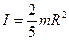
тонкого диска радиусом R и массой m относительно оси, совпадающей с диаметром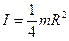

Момент инерции тела I относительно произвольной оси определяется по теореме Штейнера: 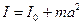, где I₀ – момент инерции тела относительно оси, параллельной данной и проходящей через центр масс, а – расстояние между осями.

Работа внешних сил при повороте твердого тела вокруг неподвижной оси: .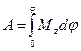

Кинетическая энергия тела, вращающегося вокруг неподвижной оси .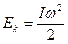

Кинетическая энергия твердого тела при плоском движении: 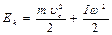, где m – масса тела, 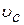- скорость центра масс, I – момент инерции относительно оси, проходящей через центр масс, 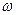– угловая скорость вращения вокруг той же оси.

Момент импульса твердого тела относительно неподвижной оси z: 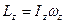, где I_z – момент инерции тела относительно оси z, 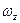– угловая скорость.

Условия равновесия твердого тела.

Результирующая всех внешних сил, приложенных к телу, должна быть равной нулю, т.е.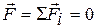

Суммарный момент внешних сил относительно любой точки должен быть равен нулю, т.е. .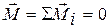

§ 5. Механика жидкостей и газов.

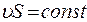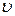Для стационарного течения несжимаемой жидкости справедливо уравнение неразрывности струи: , где - скорость жидкости, 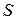- площадь поперечного сечения трубки тока.

Объем жидкости, протекающей за единицу времени через сечение 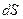с нормалью .

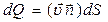Скорость истечения идеальной жидкости через малое отверстие в широком сосу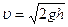де: , где 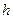- глубина отверстия относительно уровня жидкости в широком сосуде.

Уравнение Бернулли: 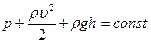, где 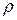- плотность жидкости, 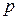- статическое давление жидкости, 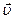- скорость течения жидкости, 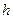- высота сечения трубки тока над некоторым уровнем.

При переходе объема 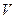жидкости из пространства, где давлением 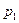, в пространство с давлением 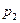, внешним давлением совершается работа: .

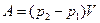При ламинарном течении жидкости, помещенное в поток тело испытывает лобовое сопротивлени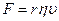е: , где 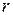- коэффициент, зависит от формы и размера тела, 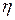- вязкость, 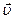- скорость потока.

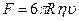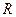При движении шара в вязкой среде сила сопротивления (формула Стокса): , где - радиус шара.

Объем 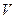жидкости, протекающей через трубку длиной 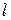и радиусом 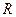при ламинарном движении за время 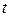, определяется по формуле Пуазейля: 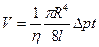, где 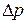- разность давлений на концах трубки.

В случае турбулентного потока при не очень больших скоростях лобовое сопротивлени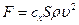е: , где 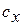- коэффициент лобового сопротивления, зависящий от формы тела и числа Рейнольдса, 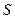- площадь проекции тела на плоскость, перпендикулярную к скорости потока, 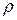- плотность среды.

Число Рейнольдса: 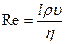, где 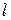- величина, характеризующая линейные размеры обтекаемого тела.

§ 6. Неинерциальные системы отсчета.

Силы инерции при ускоренном (с ускорением 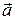) поступательном движении системы отсчета: .

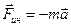Сила Кориолиса:. В случае вращающейся системы отсчета силу инерции называют центробежной силой. 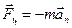, 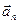- центростремительное ускорение. На движущееся со скоростью 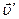во вращающейся системе отсчета тело действует также сила Кориолиса .

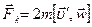Основной закон динамики для неинерциальных систем отсчета 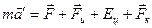, 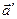- ускорение в неинерциальной системе отсчета.

§ 7. Элементы специальной теории относительности.

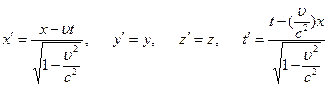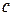Преобразования Лоренца: , где - скорость света в вакууме. Сокращение длины движущегося тела: 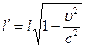, где 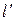- длина движущегося тела, 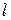- собственная длина. Замедление хода движущихся часов:

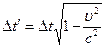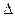
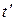, где - интервал времени между событиями в движущейся системе отсчета, 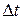- интервал времени между теми же событиями в неподвижной системе.

Релятивистский закон сложения скоростей: 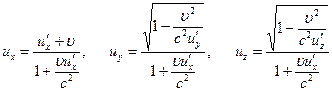, где 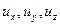- проекции скорости в неподвижной системе координат, 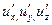- проекции скорости в движущейся системе.

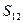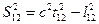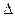
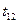Квадрат интервала - между событиями 1 и 2 инвариантная величина: , где - интервал времени между событиями 1 и 2, 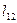- расстояние между точками 1 и 2, в которых произошли данные события.

Релятивистская масса и импульс: 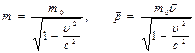, где 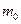- масса покоя. Кинетическая энергия движущегося тела: .

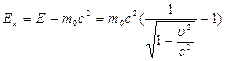Взаимосвязь массы и энергии 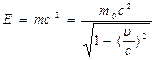, Связь между полной энергией и импульсом релятивистской частицы .

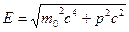§ 8. Упругие свойства тел.

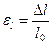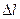Относительная продольная деформация: , где - приращение длины при растяжении или сжатии, 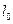- длина тела до деформации.

Относительной деформацией кручения называется отношение угла закручивания к длине стержня: .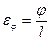

Относительное изменение объема при продольной деформации: , где 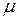- коэффициент Пуассона, равный отношению относительной поперечной деформации к продольной: .

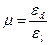Напряжение при упругой деформации: 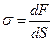, где 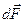- сила, действующая на сечение .

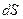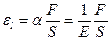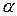Зависимость между относительной продольной деформацией и деформирующей силой (закон Гука): , где - коэффициент упругости, 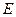- модуль Юнга.

Разрушающая сила: 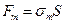, где 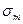- разрушающее напряжение.

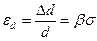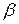Относительное изменение толщины: , где - коэффициент поперечного сжатия при продольном растяжении.

Деформация сдвига характеризуется углом сдвига, определяемым по формуле:

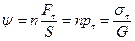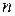, где - коэффициент сдвига, 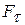- сила, вызывающая сдвиг, 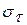- касательное напряжение, 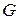- модуль сдвига.

Модуль Юнга Е, модуль сдвига 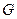и коэффициент Пуассона 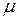связаны соотношением: 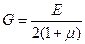. Угол закручивания стержня: 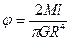, где - вращающий момент, 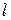- длина стержня, 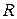- радиус стержня.

Потенциальная энергия упруго деформированного стержня: 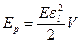, где 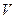- объем стержня. Плотность энергии упруго деформированного стержня: .

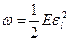§ 9. Механические колебания и волны.

Уравнение затухающих колебаний и его решени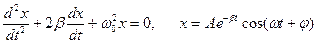е: , где 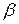- коэффициент затухания, 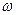- частота затухающих колебаний: 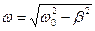. Логарифмический декремент затухания: 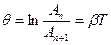. Период малых колебаний математического маятника: 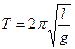, где 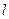- длина маятника, 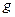- ускорение силы тяжести. Период колебаний тела, подвешенного на пружине: 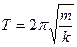, где 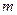- масса тела, k - жесткость пружины. Период малых колебаний физического маятника: 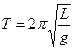, где 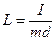- приведенная длина физического маятника, - момент инерции маятника относительно оси качания, 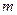- масса маятника, 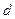- кратчайшее расстояние от центра масс до оси качания. 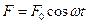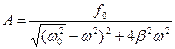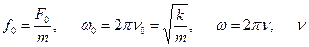Амплитуда вынужденных колебаний при действии вынуждающей силы : где и 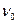- частоты собственных колебаний при отсутствии затухания и вынуждающей силы. Период колебаний однородной струны: 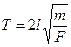, где 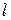- длина струны, 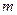- масса единицы длины струны, 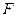- сила натяжения струны.

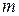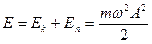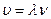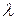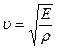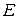Полная энергия материальной точки массой , которая совершает гармонические колебания: . Скорость распространения волны: , где - длина волны. Скорость распространения продольных волн в тонких стержнях: , где - модуль Юнга среды, 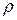- плотность материала стержня.

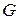Скорость распространения поперечных волн: , где - модуль сдвига.

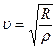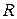Скорость продольных волн в неограниченной упругой среде: , где - модуль всестороннего сжатия.

§ 10. Закон всемирного тяготения.

Две материальные точки массам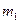и и расположенные на расстояние 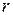, взаимодействуют (притягтваются) с силой: 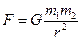, где 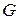- гравитационная постоянная.

При движении планет вокруг Солнца и спутников вокруг планет (в том числе и искусственных) кубы больших полуосей эллипсов пропорциональны квадратам времен обращения планет (третий закон Кеплера): 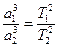, а площади, описываемые радиусом вектором планеты за равные промежутки времени равны.