Примеры решения задач.

Пример 1. Автомобиль проходит первую часть пути со скоростью 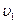, а оставшуюся часть пути со скоростью 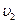=50 км/ч. Определить среднюю скорость на первом участке пути, если средняя скорость на всем пути 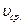=37, 5 км/ч.

Решение. Средняя скорость определяется как частное от деления всего пройденного пути на время, за которое этот путь пройден: 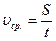. Время движения на всем пути складывается из времени движения на первом и втором участках пути: 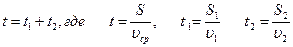, отсюда 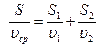. Учитывая условие задачи, получаем: 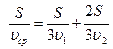.Из полученного уравнения находим .

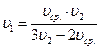Подставляя числовые значения, получим: 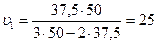км/ч.

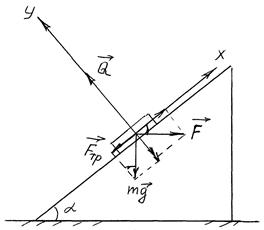
Пример 2. На тело массой 100 кг, лежащее на наклонной плоскости, которая образует с горизонтом угол 40⁰, действует горизонтальная сила 1500 Н (рис. 1). Определить: 1) силу, прижимающую тело к плоскости; 2) силу трения тела о плоскость; 3) ускорение, с которым поднимается тело. Коэффициент трения 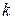=0, 10; 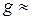10 м/с².

Найти: 1) 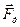- силу давления тела на плоскость; 2) 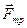- силу трения тела о плоскость; 3) 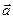- ускорение движения тела.

Решение

Выберем направление координатных осей так, чтобы одна из них была направлена вдоль наклонной плоскости (ОХ), а другая – перпендикулярно к наклонной плоскости (OY), (см. рис. 1).

На тело действуют сила 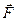- параллельно основанию наклонной плоскости, сила тяжести

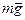- вертикально вниз, реакция плоскости 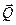Рис.1

- перпендикулярно к наклонной плоскости, и сила трения 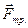- вдоль наклонной плоскости в сторону противоположную движению.

Запишем в векторной форме уравнения второго закона Ньютона для сил, действующих на тело: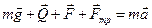

Для перехода к скалярной форме, найдём проекции всех действующих сил на координатные оси. Разложим силы 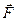и 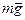на составляющие, перпендикулярные к наклонной плоскост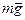и ( _y и 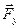) и действующие вдоль наклонной плоскост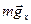и ( и 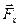). Вдоль оси OY действуют силы 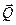, , 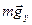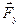. Так как в направлении OY ускорения нет, то равнодействующая этих сил равна нулю. 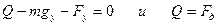- (по третьему закону Ньютона). Из чертежа видно, что 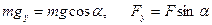Следовательно, 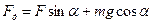. Силу трения определим по формуле: 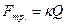. Ускорение тела вдоль оси OX найдем из соотношения 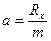, где 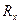- равнодействующая всех сил, действующих на тело, вдоль наклонной плоскости; она равна 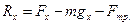. Как видно из рисунка, 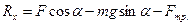. Найдем силу нормального давления и силу трения.

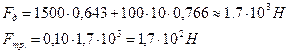
Определим ускорение: 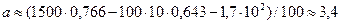м/с².

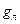
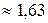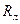
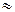
Пример 3. Определить массу и среднюю плотность вещества Луны, если ускорение свободного падения на её поверхности приблизительно равно м/с². Радиус Луны 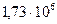м. 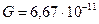м³/кг с² – гравитационная постоянная.

Решение:

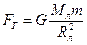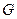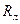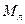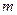Эту задачу можно решить с помощью закона всемирного тяготения: , где - гравитационная постоянная, - радиус Луны, а и - соответственно масса Луны и тела, лежащего на её поверхности. Учитывая, что на полюсах планеты (а если её вращением вокруг оси можно пренебречь, то и на других широтах) сила тяжести равна силе тяготения, получаем: 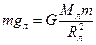, или .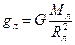

Тогда 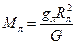. Находим массу Луны: 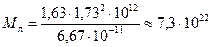кг. Среднюю плотность найдем по формуле: 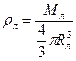. Подставляя найденное значение массы, получаем: 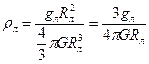; 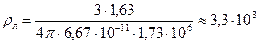кг/м³.

Пример 4. Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид 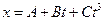, где А = 4 м, В = 2 м/с, С = -0, 5 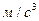. Для момента времени 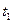= 2 с определить: координату 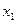точки; мгновенную скорость 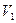; мгновенное ускорение .

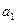Решение. Найдем координату точки, для которой известно кинематическое уравнение движения, подставив в уравнение движения вместо t заданное значение :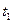

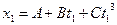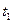; = 4 м. Мгновенную скорость 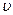в произвольный момент времени t найдем, продифференцировав координату х по времени: .

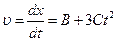Тогда в заданный момент времени мгновенная скорость: 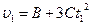; 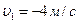. Знак минус указывает на то, что в момент времени 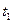= 2 с точка движется в отрицательном направлении координатной оси. Мгновенное ускорение в произвольный момент времени найдем, взяв вторую производную от координаты по времени: 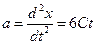. Мгновенное ускорение в заданный момент времени равно: 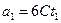; 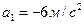. Знак минус указывает на то, что направление вектора ускорения совпадает с отрицательным направлением координатной оси.

Пример 5. Тело вращается вокруг неподвижной оси по закону, выражаемому формулой 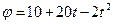. Найдите по величине и направлению полное ускорение точки, находящейся на расстоянии R = 0, 1 м от оси вращения, для момента времени 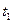= 4 с.

Решение. Точка вращающегося тела описывает окружность. Полное ускорение точки определяется геометрической суммой тангенциального и нормального ускорения:

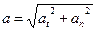. Анализ зависимости 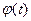указывает на то, что угловая скорость изменяется равномерно с течением времени, поэтому ускорения тела выражаются формулами: 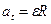, , 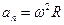где 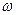— угловая скорость тела; 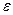— его угловое ускорение; R — расстояние от оси вращения. Подставляя выражения 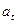и 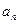, находим: 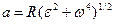. Угловая скорость вращающегося тела равна 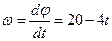. В момент времени t = 4с угловая скорость 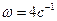. Угловое ускорение вращающегося тела равно первой производной от угловой скорости по времени: 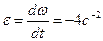. Подставляя найденные значения в формулу, получим: 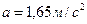. Направление полного ускорения можно определить, если найти углы, которые векторы ускорения составляют с касательной к траектории или нормалью к ней: 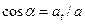. Найдем значения 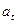и 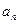: 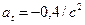; 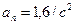. Подставив эти значения и значения полного ускорения, получим: ; .

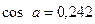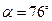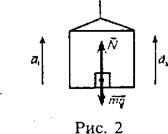Пример 6. На горизонтальной платформе шахтной клети стоит человек массой m = 60 кг (рис. 2). Определить силу давления человека на платформу: 1) при ее подъеме с ускорением 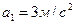; 2) при равномерном подъеме и спуске; 3) при спуске с ускорением .

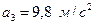Решение. На человека, стоящего на платформе шахтной клети действуют две силы: сила тяжести 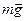и сила реакции опоры 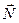. Согласно второму закону Ньютона: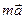 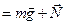. Согласно третьему закону Ньютона сила давления чело­века на платформу равна силе реакции опоры: , .

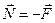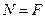1.Запишем уравнение в проекции на осьY 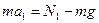. Получим , .

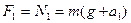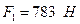2. При равномерном движении шахтной клети 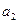=0. Следовательно, сила давления человека на платформу равна силе тяжести: .

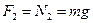3. При спуске платформы с ускорением, направленным вниз уравнение движения платформы имеет вид 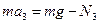. Откуда сила давления человека на платформу: 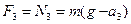. Учитывая, что 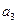= g имеем 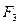= 0. Следовательно, человек не давит на платформу.

Пример 7. Каким был бы период обращения искусственного спутника Земли (ИСЗ) на круговой орбите, если бы он был удален от поверхности Земли на расстояние, равное земному радиусу (R = 6400 км).

Решение. Период обращения ИСЗ по круговой орбите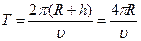

Для определения скорости спутника учтем, что при его движении по круговой орбите на спутник действует только сила притяжения Земли 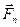сообщающая ему нормальное ускорение: 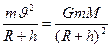; где G — гравитационная постоянная; m — масса спутника; M — масса Земли. Отсюда скорость спутника равна 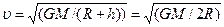. Учитывая, что 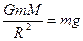, где g — ускорение силы тяжести на поверхности Земли, получаем 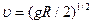. Подставляя это выражение скорости в формулу периода, найдем, что 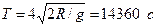= 3 ч 59 мин.

Пример 8. Стальная проволока сечением 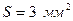под действием растягивающей силы, равной 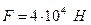имеет длину 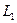= 2 м. Определить абсолютное удлинение проволоки при увеличении растягивающей силы на 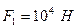. Модуль Юнга стали 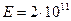Па.

Решение. Для того чтобы найти абсолютное удлинение проволоки при увеличенной растягивающей силе необходимо узнать ее первоначальную длину L. Из закона Гука 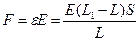. Находим 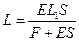. При увеличении растягивающей силы на величину 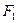: 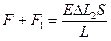. Откуда 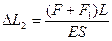.Заменив L выражением, записанным выше, получаем .

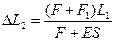Подставив данные, находим: 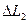= 0, 16 м.

Пример 9. Маховик, массу которого m = 5 кг можно считать распределенной по ободу радиуса r = 20 см, свободно вращается вокруг горизонтальной оси, проходящей через его центр с частотой 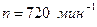. При торможении маховик останавливается через 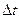= 20 с. Найти тормозящий момент М и число оборотов N, которое сделает маховик до полной остановки.

Решение. Если тормозящий момент постоянен, то движение маховика равнозамедленное, и основное уравнение динамики вращательного движения можно записать в ви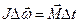де: , где 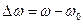— изменение угловой скорости за интервал времени 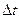; 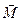— искомый тормозящий момент. Число оборотов N может быть найдено как кинематически, так и по изменению кинетической энергии, равному работе совершаемой тормозящей силой. 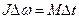, где 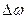, М — модули соответствующих векторов. Из условия задачи следует, что 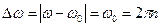. Поскольку масса маховика распределена по ободу, момент инерции 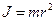. Получим 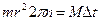. Тогда 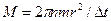= 0, 75 Н/м. Векторы 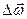, 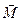направлены в сторону противоположную вектору 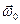. Угловое перемещение, пройденное маховиком до остановки 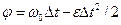.Учитывая, что 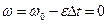преобразуем выражение

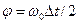. Так как 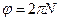, , 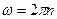где N — число оборотов, которое делает маховик до полной остановки, окончательно получим 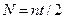= 120 об.

Пример 10. На скамье Жуковского сидит человек и держит в вытянутых руках гири массой m =10 кг каждая. Расстояние от каждой гири до оси вращения скамьи 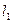= 50 см. Скамья вращается с частотой 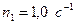. Как изменится частота вращения скамьи и какую работу А произведет человек, если он сожмет руки так, что расстояние от каждой гири до оси уменьшится до 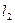= 20 см. Суммарный момент инерции человека и скамьи относительно оси вращения 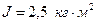. Ось вращения проходит через центр масс человека и скамьи.

Решение. Частота вращения скамьи Жуковского изменится в результате действий, производимых человеком при сближении гирь. В системе тел скамья — человек — гири все силы, кроме сил реакции опоры, являются внутренними и не изменяют момента импульса системы. Однако моменты сил реакции опоры относительно вертикальной оси равны нулю. (Для скамьи Жуковского силы трения в оси можно считать отсутствующими.) Следовательно, момент импульса этой системы остается постоянным:

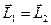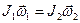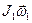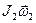; , где , — моменты импульса системы соответственно до и после сближения гирь. Перепишем в скалярном виде: 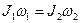. До сближения гирь момент инерции всей системы 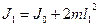. После сближения 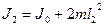, где m — масса каждой гири. Выражая угловую скорость через частоту вращения по формуле 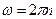и подставляя ее в уравнение получаем 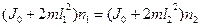. Откуда 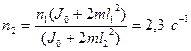. Все внешние силы не создают вращающего момента относительно оси и, следовательно, не совершают работы. Поэтому изменение кинетической энергии системы равно работе, совершенной человеком: 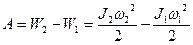. Учитывая, что 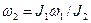, получаем работу, совершаемую человеком: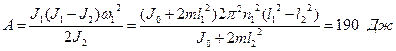

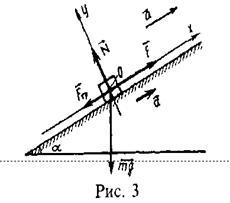
Пример 11. Автомобиль массой m = 2000 кг движется вверх по наклонной плоскости с уклоном

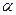= 0, 1 (рис. 3), развивая на пути S = 100 м скорость 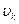= 36 км/ч. Коэффициент трения 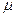= 0, 05. Найти среднюю и максимальную мощность двигателя автомобиля при разгоне.

Решение. Автомобиль движется равноускоренно, причем начальная скорость равна нулю. Выберем ось х, расположенную вдоль наклонной плоскости, ось у — перпендикулярно ей

На автомобиль действует четыре силы: сила тяжести 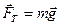, сила реакции опоры 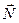, сила тяги 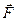и сила трения 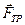. Запишем основной закон динамики: 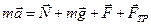. Это уравнение в проекциях на оси координат: на ось х: 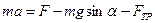, на ось у: 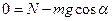, 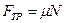. Выразим из этих уравнений силу тяги 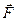: 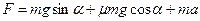. Ускорение 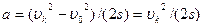Найдем работу двигателя на этом участк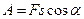е: , где 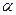— угол между 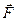и 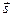равен нулю. Подставив сюда выражение для 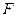, получим 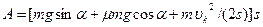. Средняя мощность равна 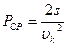, откуда 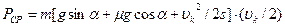. Максимальная мощность автомобиля достигается в тот момент, когда скорость максимальна: , ,

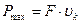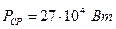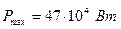
Пример 12. Деревянный стержень массой М = 6, 0 кг и длиной 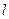= 2, 0 м может вращаться в вертикальной плоскости относительно горизонтальной оси. В конец стержня попадает пуля массой m = 10 г, летящая со скоростью 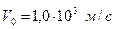, направленной перпендикулярно стержню и застревает в нем. Определить кинетическую энергию стержня после удара.

Решение. Физическая система образована из двух тел: стержня и пули. Пулю можно считать за материальную точку, стержень примем за твердое тело. Пуля до взаимодействия двигалась прямолинейно, а после взаимодействия вместе со стержнем вращается вокруг неподвижной оси. Применим закон сохранения момента импульса относительно этой оси. Условия применимости этого закона — замкнутость системы выполнены. 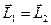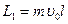По закону сохранения момента импульса: , где — момент импульса пули относительно оси вращения до удара; 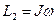— момент инерции стержня и пули относительно оси вращения. 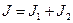, где 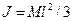— момент инерции стержня; 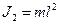— момент инерции пули.

Учитывая вышеизложенное, получим 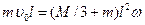. Так как m < < М, можно приближенно считать, что 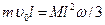, откуда .

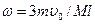Кинетическая энергия стержня 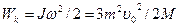= 25 Дж.

Пример 13. Определить релятивистский импульс р и кинетическую энергию электрона, движущегося со скоростью 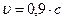(где с — скорость света в вакууме).

Решение. Релятивистский импульс 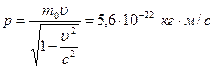. В релятивистской механике кинетическая энергия определяется как разность между полной энергией W и энергией покоя 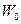. . 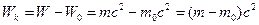Получим .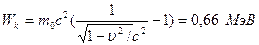