
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Глава I
|
|
Обработка данных наблюдений и проверка гипотез
Задание: В результате независимых измерений получены n значений ошибки точности настройки РПУ на заданную частоту: х1, х2, …хn. Произвести полный статистический анализ данных выборки и сделать соответствующие выводы.
Значения выборки
| 0, 637 | 1, 121 | 0, 409 | 1, 082 | -0, 263 |
| 0, 267 | 1, 627 | 0, 061 | -1, 114 | -0, 529 |
| -0, 142 | 0, 658 | -0, 964 | -0, 586 | 0, 799 |
| -0, 394 | -0, 036 | 0, 507 | 0, 882 | -0, 856 |
| -0, 118 | 0, 678 | -1, 414 | 0, 679 | -0, 276 |
| 0, 247 | 1, 469 | -0, 847 | -0, 032 | 0, 379 |
| -0, 973 | 0, 522 | -1, 191 | 0, 091 | 1, 468 |
| 0, 486 | 1, 642 | 0, 185 | 0, 838 | -1, 805 |
| 0, 820 | -0, 872 | -0, 090 | -0, 304 | -0, 266 |
| -0, 426 | -0, 358 | -0, 866 | -2, 716 | -0, 592 |
| 0, 243 | 1, 594 | -1, 116 | 0, 823 | -1, 473 |
| -0, 822 | 0, 109 | -0, 156 | -1, 248 | -1, 266 |
| 0, 238 | 0, 676 | -1, 387 | 0, 346 | 0, 702 |
| -0, 220 | -1, 084 | -0, 406 | -0, 537 | 1, 071 |
| -1, 566 | 0, 318 | -0, 454 | -0, 402 | -0.383 |
| 0, 932 | 0, 367 | 0, 575 | 1, 214 | 0.167 |
| -0, 833 | -0, 992 | -0, 266 | -1, 214 | -0, 348 |
| -0, 039 | 0, 529 | 1, 246 | 1, 353 | 0, 192 |
| 0, 275 | 0, 278 | 0, 557 | 1, 511 | -1, 447 |
| -0, 163 | 1, 392 | 0, 004 | -0, 184 | 0, 495 |
min=
max=
Статическое распределение выборки
1. По данным выборки найти:
а) размах варьирования: R = xmax – xmin,
R= 1, 642-(-2.716)= 4, 4
б) количество интервалов (разрядов):
к=7
в) длину разряда: 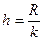
h= 0, 6
Интервал (-2, 7; 1, 6) расширим до интервала (-3; 1, 9). Сдвиг в каждую стороны при этом не превысит: 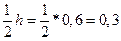
Для нового интервала изменения признака (-3; 1, 9) приk= 7 длина разряда получается равной 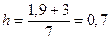
2. Произведем группировку опытных данных и построим интервальный вариационный ряд. Расчет оформим в виде таблицы 1.
Таблица №1
| Границы интервала | [-3; -2, 3) | [-2, 3; -1, 6) | [-1, 6; -0, 9) | [-0, 9; -0, 2) | [-0, 2; 0, 5) | [0, 5; 1, 2) | [1, 2; 1, 9) |
Частот
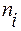 
| |||||||
Относительные частоты 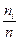
| 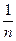
| 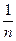
| 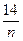
| 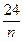
| 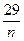
| 
| 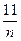
|
Накопленные частоты ∑ 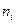
|
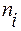
 -
-
n -
Расчет сводных характеристик выборки
1. Вычислим моду 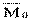 и медиану
и медиану 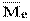 выборочного распределения.
выборочного распределения.
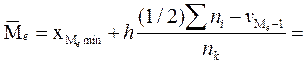
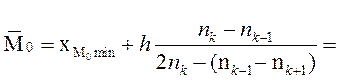
2. По интервальному вариационному ряду, полученному в §1 составить дискретный вариационный ряд в виде таблицы 2, в котором в качестве вариант берём середины разрядов
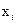
| |||||||
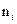
|
Таблица № 2




Вычислим выборочную среднюю 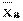 (математическое ожидание) и выборочную дисперсию
(математическое ожидание) и выборочную дисперсию 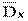 :
:
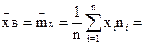
| 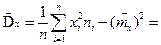
|
3. Для расчета сводных характеристик выборки по методу произведений составим таблицу 3.
Таблица № 3
h=
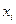
| 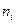
| 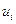
| 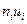
| 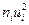
| 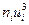
| 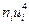
| 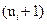
| 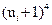
| 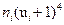
|
| ∑ | ∑ | ∑ | ∑ | ∑ | ∑ |
Контроль расчетов производим по формуле:
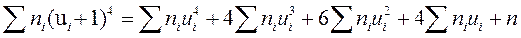
4. Вычислим начальные условные эмпирические моменты:
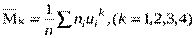
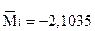

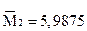

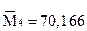
5. Используя начальные моменты 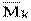 , вычислим центральные моменты:
, вычислим центральные моменты:
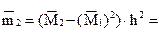
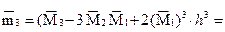
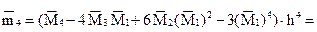
6. Найдем выборочную среднюю (выборочное математическое ожидание):
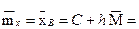
где, С = 0, 09
7. Вычислим выборочную дисперсию и исправленную выборочную дисперсию:
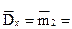
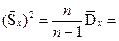
8. Найдем выборочное среднее квадратическое отклонение (с.к.о.) и исправленное выборочное с.к.о.:
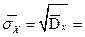
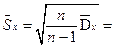
9. Определим, чему равны выборочная асимметрия и выборочный эксцесс:
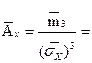
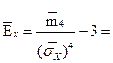
Расчет интервальных оценок генеральных параметров
Построим доверительные интервалы для оценки генерального математического ожидания mx и генерального с.к.о. σ х. Для этого по заданной доверительной вероятности (надежности) γ из таблицы функции Лапласа найдем значение аргумента tγ этой функции, для которого Ф(tγ ) = γ.
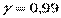
| 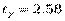
| 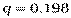
|
Используя найденное tγ , рассчитаем границы доверительного интервала для
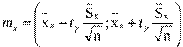
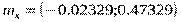
Интервальную оценку генерального с. к. о. определим по одной из формул:
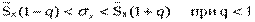
| 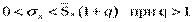
|
| В данном варианте q< 1 то < σ x< |
Проверка гипотезы о нормальном распределении
генеральной совокупности по критерию Пирсона
Для того, чтобы при заданном уровне значимости α = 1 – γ проверить гипотезу о нормальном распределении обследуемого признака X генеральной совокупности, заполним таблицу 5.
Таблица №5
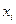
| 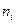
| 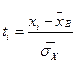
| 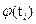
| 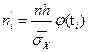
| 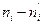
| 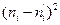
| 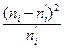
| 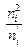
|
| ∑ | ∑ |
Контроль вычислений производим по формуле:
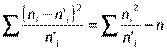
Обозначим сумму элементов восьмого столбца 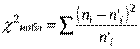 , и для заданного уровня значимости α числа свободы р = k – 3 находим критическую
, и для заданного уровня значимости α числа свободы р = k – 3 находим критическую
точку 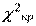 (α; р)
(α; р)
ВЫВОД: так как 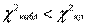 , то нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности. Другими словами, эмпирические и теоретические частоты различаются незначимо (случайно).
, то нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности. Другими словами, эмпирические и теоретические частоты различаются незначимо (случайно).
Построение гистограммы выборки и теоретической
нормальной кривой
1. Для построения гистограммы в выбранной системе координат на оси абсцисс откладываем разряды, а на каждом из разрядов как на основании строим прямоугольник с высотой 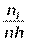 , составляя таблицу 6.
, составляя таблицу 6.
Таблица №6
| Разряды | ||||||||||
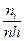
|
На этом же графике строим гипотетическую (предположительную) теоретическую нормальную кривую. Для этого берем середины разрядов х i и выравнивающие частоты ni из таблицы 5. Эти данные заносим в таблицу 7.
Таблица №7
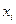
| ||||||||||
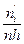
|
наносим точки с координатами 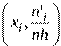 и соединяем их плавной линией, получая искомую кривую.
и соединяем их плавной линией, получая искомую кривую.
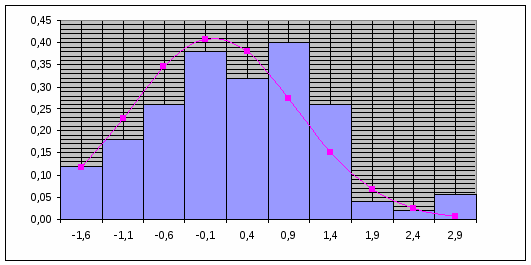
ВЫВОД: В данной части курсовой работы проверена гипотеза Пирсона, ее нет оснований отвергнуть, другими словами, эмпирические и теоретические частоты различаются незначимо (случайно).
| Разряды | -1.6 | -1.1 | -0.6 | -0.1 | 0.4 | 0.9 | 1.4 | 1.9 | 2.4 | 2.9 |
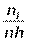
| 0, 12 | 0, 18 | 0, 26 | 0, 38 | 0, 32 | 0, 40 | 0, 26 | 0, 04 | 0, 02 | 0, 06 |
В последней строке результаты вычислений округлим до 0, 01.
На этом же графике строим гипотетическую (предположительную) теоретическую нормальную кривую. Для этого берем середины разрядов х i и выравнивающие частоты ni из таблицы 5. Эти данные заносим в таблицу 7.
Таблица №7
| xi | -1.6 | -1.1 | -0.6 | -0.1 | 0.4 | 0.9 | 1.4 | 1.9 | 2.4 | 2.9 |
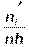
| 0, 12 | 0, 23 | 0, 35 | 0, 41 | 0, 38 | 0, 27 | 0, 15 | 0, 07 | 0, 024 | 0, 006 |
наносим точки с координатами 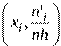 и соединяем их плавной линией, получая искомую кривую.
и соединяем их плавной линией, получая искомую кривую.
