
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тригонометрические ряды Фурье для функций нескольких переменных
|
|
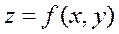 - дана функция.
- дана функция.
Сначала, разложим ее по х, в комплексный ряд Фурье
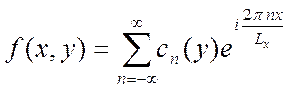 на
на 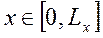 .
.
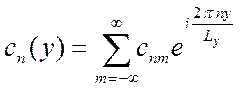 ,
, 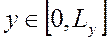 .
.
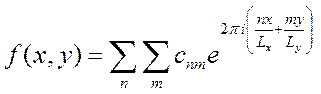 ,
,
где
 (41)
(41)
так же и большее число переменных.
Понятие интеграла Фурье
Предположим, что функция f(x) является кусочно-гладкой и периодической с периодом T=2l, кроме того определим функцию в точках разрыва
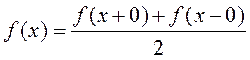 (1)
(1)
Тогда периодическая функция f(x) является непрерывной и имеет непрерывную производную на всей числовой оси, за исключением, может быть, конечного числа точек на отрезке [-l, l]. Кроме того, в этих точках существуют конечные пределы f(x) и f /(x) слева и справа. Множество, обладающее такими свойствами, обозначим через L1. Каждую такую функцию можно представить рядом Фурье
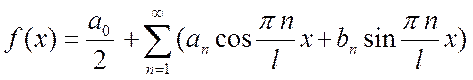 (2)
(2)
коэффициенты которого определяются по формулам
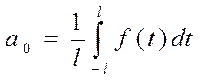 (3)
(3)
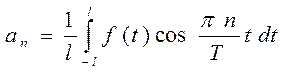 (4)
(4)
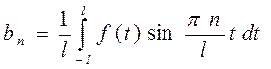 (5)
(5)
Исследуя ряд Фурье, мы доказали, что ряд Фурье сходится к f(x). Предположим, что функция f(x) является непериодической и кусочно-гладкой. Выражение интеграла Фурье получим из ряда Фурье периодической функции f(x). Для этого в ряд (32) подставим выражение коэффициентов a0, an и bn  (6)
(6)
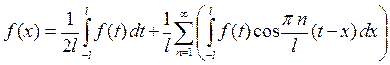
Введём обозначения:
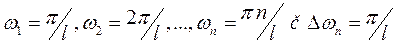 ,
,
тогда
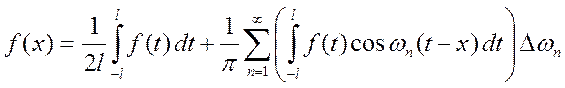
Пусть 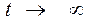 (функция из периодической становится непериодической).
(функция из периодической становится непериодической).
Очевидно, что
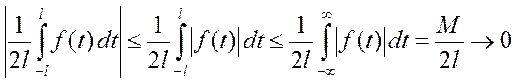
Второе слагаемое из (6) с учётом обозначений

приводится к виду
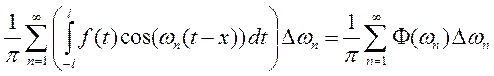
В таком виде эта сумма напоминает интегральную сумму функций 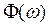 на отрезке
на отрезке 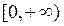 .Перейдя к пределу при
.Перейдя к пределу при 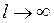 , получаем
, получаем
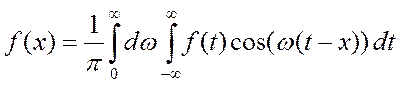
Это выражение назовём двойным интегралом Фурье для непериодической функции  .
.
Преобразуем интеграл Фурье следующим образом

Обозначим
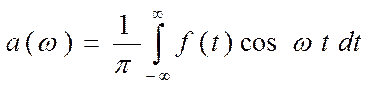
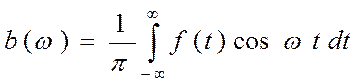
Тогда
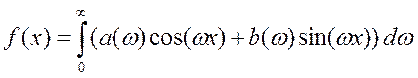
В таком виде интеграл Фурье похож на ряд Фурье. Суммирование по дискретному параметру 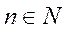 заменено интегрированием по непрерывно меняющему параметру
заменено интегрированием по непрерывно меняющему параметру 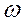 .
.
Коэффициенты 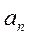 и
и 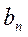 аналогичны коэффициентам
аналогичны коэффициентам 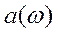 и
и 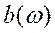 .
.
Интеграл Фурье для чётных функций
1. Предположим, что 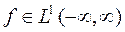 и является чётной функцией. Очевидно, что
и является чётной функцией. Очевидно, что 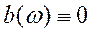 и
и
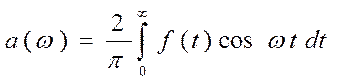 (7)
(7)
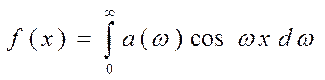 (8)
(8)
2. Пусть 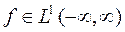 и является нечётной функцией.
и является нечётной функцией.
Тогда  и
и
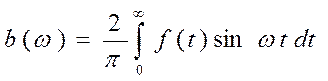 (9)
(9)
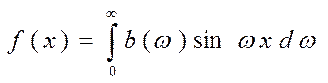 (10)
(10)
Если функция f определена на 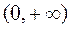 или
или 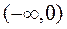 , то целесообразно её доопределить на другой половине оси таким образом, чтобы она была чётной или нечётной. Тогда сможем использовать представленные формулы (7)-(10). В свою очередь эти формулы можно представить в другой симметричной форме. С этой целью обозначим
, то целесообразно её доопределить на другой половине оси таким образом, чтобы она была чётной или нечётной. Тогда сможем использовать представленные формулы (7)-(10). В свою очередь эти формулы можно представить в другой симметричной форме. С этой целью обозначим
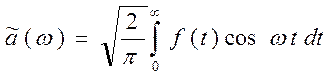 (11)
(11)
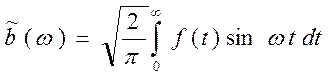 (12)
(12)
Тогда формулы (8) и (10) принимают вид
 (13)
(13)
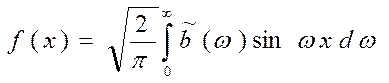 (14)
(14)
Функцию 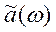 называют косинус-преобразованием Фурье функции f, а
называют косинус-преобразованием Фурье функции f, а 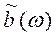 - синус-преобразованием Фурье.
- синус-преобразованием Фурье.